Шестиугольник – это геометрическая фигура, состоящая из шести сторон и шести углов. Описанный около окружности шестиугольник означает, что все его вершины лежат на окружности. Периметр – это сумма длин всех сторон фигуры. Нахождение периметра шестиугольника описанного около окружности может представлять некоторую сложность, но с помощью определенных формул и правил можно справиться с этой задачей.

При решении задачи по нахождению периметра шестиугольника описанного около окружности, необходимо знать радиус данной окружности. Запишем формулу для нахождения периметра шестиугольника:

Периметр шестиугольника = длина стороны шестиугольника × 6

Учитывая, что все вершины шестиугольника лежат на окружности, можно определить радиус данной окружности с помощью различных методов. Зная радиус и применив формулу для нахождения периметра, получим искомое значение.

Определение и свойства шестиугольника

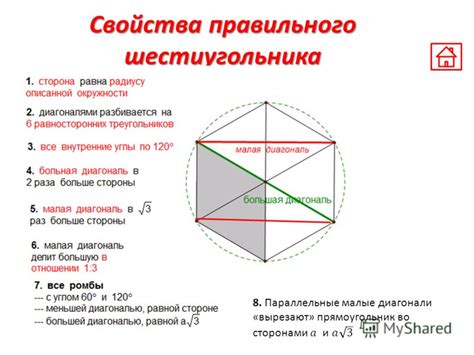
Основными свойствами шестиугольника являются:

1. Углы: Шестиугольник имеет шесть углов, сумма которых всегда равна 720 градусам. Каждый угол шестиугольника равен 120 градусам.
2. Стороны: Шестиугольник имеет шесть сторон, которые могут быть равными или неравными. Если все стороны шестиугольника равны, то он называется правильным шестиугольником.
3. Диагонали: Шестиугольник имеет диагонали – линии, соединяющие вершины, которые не являются соседними. В шестиугольнике может быть 9 диагоналей.
4. Периметр: Периметр шестиугольника – это сумма длин всех его сторон.

Шестиугольники часто встречаются в различных областях, включая математику, архитектуру и биологию. Они имеют уникальные свойства и обладают красивой симметрией, что делает их интересными объектами исследования.

Что такое описанная около окружности?

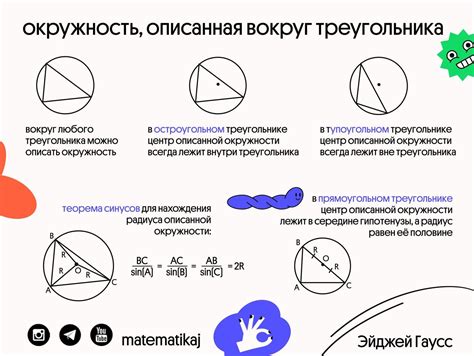
Описанная около окружность обладает несколькими важными свойствами:

1. Центр описанной около окружности совпадает с центром шестиугольника.
2. Радиус описанной около окружности равен расстоянию от центра шестиугольника до любой его вершины.
3. Периметр шестиугольника описанного около окружности можно выразить через радиус этой окружности с помощью формулы: P = 6 * r, где P - периметр, r - радиус.

Использование описанной около окружности позволяет упростить вычисления и строительство шестиугольника, так как все его вершины лежат на одной окружности.

Свойства и формулы периметра

• Все стороны равны между собой. Поэтому, если известна длина одной стороны, периметр можно найти умножив ее на 6.
• Если радиус окружности, описанной вокруг шестиугольника, известен, то его периметр можно найти, умножив радиус на 2π (число π приближенно равно 3,14).
• Если известен диаметр окружности, описанной вокруг шестиугольника, периметр можно найти, умножив диаметр на π.

Используя эти простые формулы, можно легко найти периметр шестиугольника описанного около окружности и использовать его для решения различных задач.

Пример задачи на нахождение периметра

Дано: шестиугольник описаный около окружности.

Задача: найти периметр данного шестиугольника.

1. Найти длину стороны шестиугольника. Для этого можно воспользоваться формулой:

• Диаметр окружности, описанной вокруг шестиугольника, равен двум радиусам окружности.
• Радиус окружности найдем, разделив диаметр на 2.
• Зная радиус окружности, можем найти длину стороны шестиугольника, умножив радиус на 2.

Таким образом, мы можем решить задачу на нахождение периметра шестиугольника описанного около окружности, зная диаметр окружности.