Поиск периметра шестиугольника с известным радиусом вписанной окружности можно провести с использованием простых математических формул и свойств этой геометрической фигуры. Шестиугольник, как и любой другой многоугольник, имеет некоторые характеристики, такие как углы, стороны и диагонали. В данной задаче мы будем рассматривать правильный шестиугольник, у которого все стороны и углы равны между собой.
Для начала, определимся с понятием вписанной окружности. Вписанная окружность - это окружность, которая касается всех сторон шестиугольника внутренним образом. Чтобы найти радиус вписанной окружности, можно воспользоваться формулой, которая связывает радиус окружности с длиной стороны шестиугольника. Формула имеет вид: R = a / (2 * tg(π/6)), где a - длина стороны шестиугольника, π - математическая постоянная (пи).
Зная радиус вписанной окружности, мы можем найти длину стороны шестиугольника. Длина каждой стороны равна удвоенному радиусу окружности, умноженному на тангенс угла, равного π/6. Обозначим длину стороны как a. Тогда формула имеет вид: a = 2 * R * tg(π/6). Теперь мы можем найти периметр шестиугольника, сложив длины всех его сторон: P = 6 * a.
О чем будет статья
В данной статье рассматривается способ нахождения периметра шестиугольника, в который вписана окружность с заданным радиусом. Описывается метод, основанный на использовании геометрических свойств вписанного шестиугольника и его радиуса. Дается подробное объяснение каждого шага решения задачи.
Определение периметра шестиугольника с известным радиусом вписанной окружности является важной задачей в геометрии. Это позволяет определить длину всех сторон шестиугольника, что является основой для решения различных практических задач.
С помощью данного метода вы сможете легко находить периметр шестиугольника, даже если изначально известен только радиус вписанной окружности. Знание данного метода поможет вам в решении геометрических задач и позволит более эффективно применять геометрические концепции в различных областях.
Чтобы приступить к решению задачи, необходимо узнать формулу для нахождения периметра шестиугольника с известным радиусом вписанной окружности. Затем следует проиллюстрировать геометрические свойства задачи и предложить алгоритм для поиска периметра шестиугольника.
Данный метод имеет широкое применение в различных областях, включая строительство, архитектуру, машиностроение и другие. Знание данного метода позволит вам более глубоко понять принципы геометрии и использовать их в практических задачах.
Внимание! Для успешного решения задачи необходимо понимание базовых геометрических понятий и операций, таких как нахождение площади фигур, вычисление длин сторон и использование формул. Если у вас есть затруднения в данных областях, рекомендуется повторить математический материал перед началом работы с данной задачей.
Шестиугольник и окружность
Окружность – это геометрическое место точек, равноудаленных от центра. Вписанная окружность – это окружность, которая касается всех сторон шестиугольника и полностью лежит внутри него.
Когда известен радиус вписанной окружности шестиугольника, возникает задача вычисления его периметра. Для этого существует формула: периметр шестиугольника равен произведению длины его стороны на шестерку (6).
Периметр шестиугольника можно найти, зная радиус вписанной окружности, с помощью формулы:
Периметр = 6 * Длина стороны
Для вычисления длины стороны шестиугольника, зная радиус вписанной окружности, можно воспользоваться формулой:
Длина стороны = 2 * Радиус * tg(30°)
Таким образом, зная радиус вписанной окружности, мы можем легко найти периметр шестиугольника. Это позволяет нам легко решать различные геометрические задачи, связанные с шестиугольником и окружностью.
Что такое шестиугольник и окружность
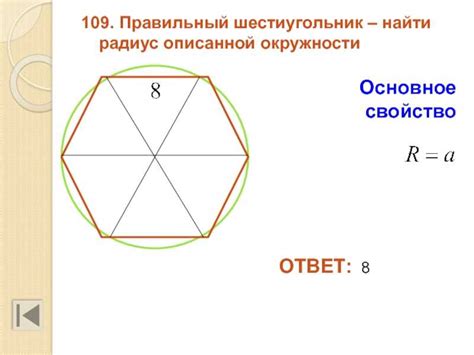
Окружность - это плоская геометрическая фигура, которая состоит из всех точек на плоскости, равноудаленных от одной фиксированной точки, называемой центром окружности. Расстояние от центра окружности до любой ее точки называется радиусом окружности.
В геометрии шестиугольник и окружность могут взаимодействовать друг с другом, так как шестиугольник может быть вписан в окружность. В этом случае, все вершины шестиугольника будут лежать на окружности, а его стороны будут касаться окружности.
Используя радиус вписанной окружности, можно найти периметр шестиугольника. У шестиугольника все стороны равны между собой, поэтому периметр будет равен шести произведениям радиуса на 2π.
| Что | Такое |
| Шестиугольник | Плоская геометрическая фигура с шестью сторонами и углами одинаковой длины и величины. |
| Окружность | Плоская геометрическая фигура, состоящая из всех точек на плоскости, равноудаленных от центра окружности. |
| Периметр | Сумма длин всех сторон фигуры. |
| Радиус вписанной окружности | Расстояние от центра окружности до любой точки на ее границе. |
Вписанная окружность
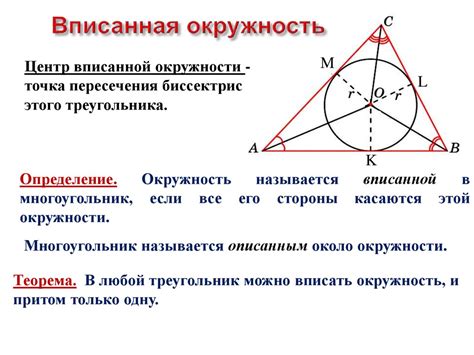
Вписанная окружность имеет ряд особенностей:
- Радиус вписанной окружности является одной из величин, которую можно измерить в шестиугольнике.
- Длина каждой стороны шестиугольника является диаметром вписанной окружности.
- Перпендикуляр, проведенный из центра вписанной окружности к любой стороне шестиугольника, делит эту сторону пополам.
- Площадь шестиугольника можно выразить через радиус вписанной окружности: S = 3√3 × r², где S - площадь шестиугольника, r - радиус вписанной окружности.
Зная радиус вписанной окружности, можно легко вычислить периметр шестиугольника по следующей формуле: P = 2 × 6 × r = 12 × r, где P - периметр шестиугольника, r - радиус вписанной окружности.
Использование вписанной окружности позволяет находить связанные параметры шестиугольника, такие как площадь или периметр, и приложить их в решении практических задач.
Радиус вписанной окружности
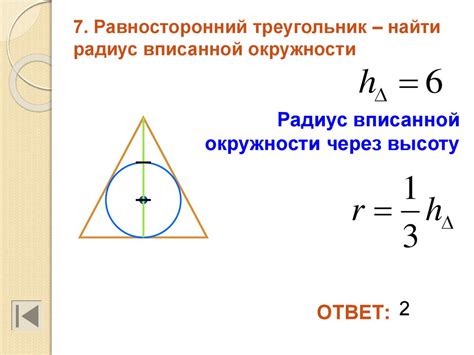
Радиус вписанной окружности важен для решения задач по нахождению периметра шестиугольника и его площади. Он также является ключевым показателем при анализе геометрических свойств шестиугольника.
Для нахождения радиуса вписанной окружности в шестиугольнике с известной длиной стороны или периметром можно воспользоваться следующей формулой:
Радиус (r) = (Сторона (s)) / (2 * √3)
где Сторона (s) - длина любой стороны шестиугольника.
Если известна площадь шестиугольника (Площадь (A)), то можно воспользоваться следующей формулой для нахождения радиуса:
Радиус (r) = √(3 * Площадь (A)) / (6 * √3)
Зная радиус вписанной окружности, можно решать дополнительные задачи, например, нахождение длин биссектрис или площадей треугольников внутри шестиугольника.
Таким образом, радиус вписанной окружности является важным геометрическим параметром при работе с шестиугольниками и позволяет проводить различные вычисления и анализы.
Периметр шестиугольника
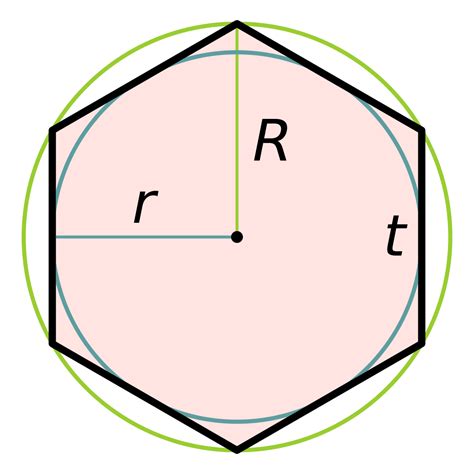
- Найдите длину одной стороны шестиугольника. Для этого можно воспользоваться теоремой Пифагора или теоремой косинусов.
- Если шестиугольник правильный, то все его стороны будут равны.
- Умножьте длину одной стороны на 6, чтобы получить периметр шестиугольника.
Например, если известно, что радиус вписанной окружности шестиугольника равен 5, то можно использовать формулу для вычисления длины стороны:
Длина стороны = 2 * радиус * sin(π/6)
Подставляя значения в формулу, получим:
Длина стороны = 2 * 5 * sin(π/6) = 10 * 0.5 = 5
Таким образом, периметр шестиугольника будет равен:
Периметр = 5 * 6 = 30
так как все стороны равны между собой в правильном шестиугольнике.
Как найти периметр шестиугольника
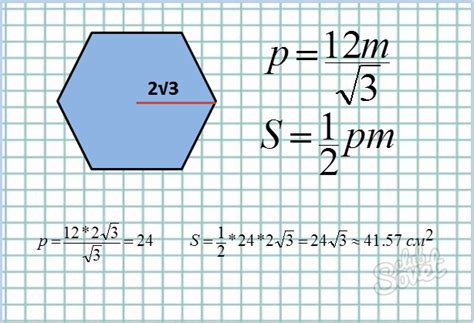
Периметр шестиугольника можно найти, зная длину одной его стороны. Для этого нужно умножить длину стороны на шесть, так как шестиугольник имеет шесть одинаковых сторон.
P = 6 * r,
где P - периметр шестиугольника, а r - радиус вписанной окружности.
Таким образом, чтобы найти периметр шестиугольника, необходимо умножить радиус вписанной окружности на шесть.
Формула периметра шестиугольника
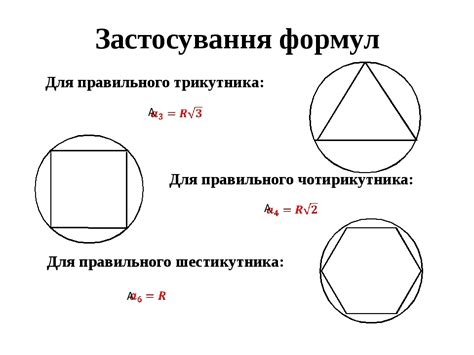
Для нахождения периметра шестиугольника с известным радиусом вписанной окружности, можно использовать следующую формулу:
П = 6 * a
где:
- П - периметр шестиугольника
- a - длина стороны шестиугольника
Таким образом, чтобы найти периметр шестиугольника, нужно умножить длину одной стороны на 6.
Например, если известно, что радиус вписанной окружности равен 5, то длина стороны шестиугольника будет равна 10 (так как она равна двойному радиусу), и периметр шестиугольника будет равен 60 (10 * 6).
Формула периметра шестиугольника позволяет быстро и просто вычислить периметр данной фигуры по известному радиусу вписанной окружности, что может быть полезно при решении различных геометрических задач.
Нахождение периметра шестиугольника с вписанной окружностью
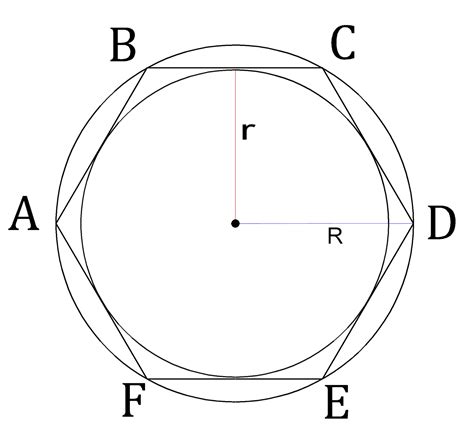
Для начала, посчитаем длину одной стороны шестиугольника. Поскольку шестиугольник равносторонний, все его стороны равны друг другу. То есть, для нахождения длины одной стороны, нужно разделить периметр шестиугольника на количество его сторон.
Длина одной стороны равно периметру шестиугольника, деленному на 6.
Затем, умножим длину одной стороны на 6, чтобы получить полный периметр шестиугольника:
Периметр шестиугольника = Длина одной стороны * 6
Таким образом, если у нас есть радиус вписанной окружности, мы можем найти периметр шестиугольника.
Применение этой формулы позволяет легко и быстро вычислить периметр шестиугольника с вписанной окружностью. Важно помнить, что все стороны шестиугольника и радиус вписанной окружности должны быть измерены в одной и той же единице измерения.
Связь между радиусом окружности и стороной шестиугольника
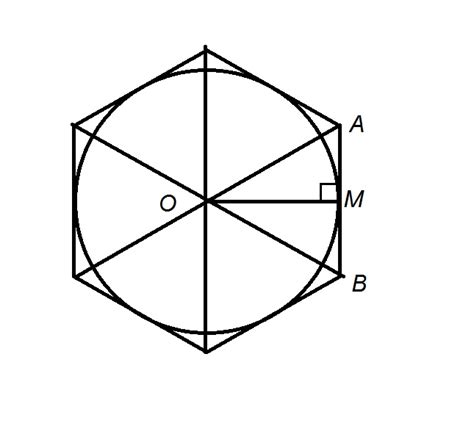
Связь между радиусом и стороной шестиугольника описывается следующей формулой:
Сторона шестиугольника = 2 * Радиус * tg(π/6)
Здесь π/6 представляет собой угол, образованный вершиной шестиугольника и центром вписанной окружности.
Тангенс (tg) этого угла можно представить следующей формулой:
tg(π/6) = 1 / √3
Из этих формул можно заключить, что сторона шестиугольника пропорциональна радиусу вписанной окружности. Чем больше радиус окружности, тем больше сторона шестиугольника, и наоборот.
Таким образом, зная радиус вписанной окружности, можно вычислить сторону шестиугольника и далее найти его периметр.