Вписанный шестиугольник – это фигура, которая описывается вокруг окружности, при этом все его вершины лежат на этой окружности. Периметр вписанного шестиугольника является одной из его основных характеристик, которая позволяет определить длину его границы. Нахождение периметра является важной задачей для многих задач и исследований в различных областях, включая геометрию, физику, инженерию и многие другие.

Для нахождения периметра вписанного шестиугольника нужно знать длину его стороны. Длина стороны шестиугольника может быть найдена с помощью различных методов и формул, например, с использованием радиуса вписанной окружности или через длины его сторон. Знание длины стороны позволит вычислить периметр шестиугольника, который представляет собой сумму длин всех его сторон.

Нахождение периметра вписанного шестиугольника может быть полезно при решении различных задач. Например, при проектировании строений или конструкций, где необходимо учесть форму и размеры фигур. Также это может быть полезно при решении геометрических задач, когда требуется найти длины отрезков или расстояния между точками, лежащими на границе шестиугольника.

Шестиугольник: периметр

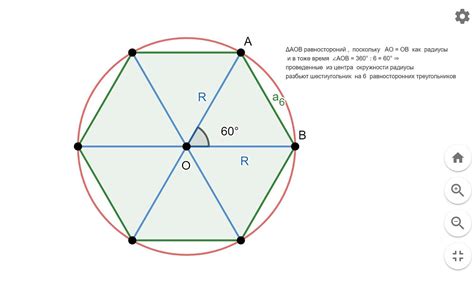
Для нахождения периметра вписанного шестиугольника можно использовать следующую формулу:

Где P обозначает периметр, а a - длину одной стороны шестиугольника.

Например, если длина одной стороны шестиугольника равна 5 см, то его периметр будет равен:

P = 6 * 5 = 30 см

Таким образом, периметр вписанного шестиугольника можно найти, умножив длину одной стороны на 6.

Что такое шестиугольник?

Шестиугольники можно найти в различных аспектах жизни, включая природные формации, кристаллы и геометрические фигуры. Например, медоносные пчелы строят свои соты в форме шестиугольников, так как эта форма позволяет им оптимально использовать пространство и максимально экономно распределять материал.

Шестиугольники также используются в архитектуре для создания крепких и устойчивых конструкций. Например, многогранник Гексагон из шестиугольников был использован в строительстве Гринченского кирпичника в Швейцарии. Это здание имеет отличные строительные качества благодаря своей гексагональной форме.

В общем, шестиугольник является уникальной геометрической фигурой, которая обладает свойствами прочности и оптимального использования пространства. Его форма встречается в различных областях природы и архитектуры, делая его важным объектом изучения геометрии.

Что такое вписанный шестиугольник?

У вписанного шестиугольника есть ряд свойств, которые делают его интересным и полезным для решения различных задач. Например, вписанный шестиугольник является одним из трех правильных многоугольников, в которых можно провести вписанную окружность.

Для вписанного шестиугольника характерны следующие свойства:

1. Все стороны вписанного шестиугольника равны между собой.
2. Сумма всех углов вписанного шестиугольника равна 720 градусов.
3. Сумма противоположных углов вписанного шестиугольника равна 180 градусов.

Вписанный шестиугольник широко используется в геометрии и математике, а также в различных областях, включая архитектуру, дизайн и технику. Его свойства и симметрия делают его инструментом для построения и разрешения геометрических и логических задач.

Свойства вписанного шестиугольника

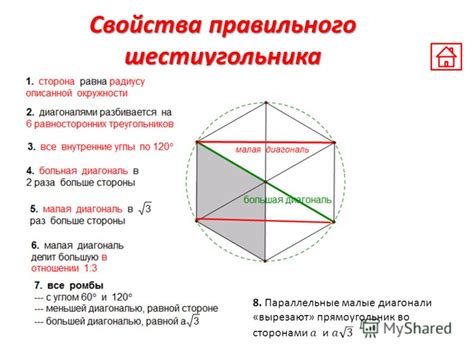
1. Вписанный шестиугольник

Вписанный шестиугольник - это шестиугольник, все вершины которого лежат на окружности.

2. Радиус окружности

Радиус окружности, на которой лежат вершины вписанного шестиугольника, является расстоянием от центра окружности до любой вершины шестиугольника.

3. Углы вписанного шестиугольника

Углы вписанного шестиугольника равны между собой и равны углу сектора окружности, в котором он вписан.

4. Диагонали вписанного шестиугольника

Диагонали вписанного шестиугольника - это отрезки, соединяющие его невершины. Диагонали вписанного шестиугольника делят его на треугольники.

5. Площадь вписанного шестиугольника

Площадь вписанного шестиугольника можно найти, разделив его на треугольники и вычислив их площади. Еще один способ - использовать формулу площади вписанного шестиугольника по радиусу окружности.

6. Периметр вписанного шестиугольника

Периметр вписанного шестиугольника - это сумма длин его сторон. Для нахождения периметра можно использовать формулу периметра шестиугольника или вычислить сумму длин всех сторон.

Изучение свойств вписанного шестиугольника поможет понять его особенности и применение в различных геометрических исследованиях и задачах.

Формула для нахождения периметра вписанного шестиугольника

Периметр вписанного шестиугольника можно найти с помощью следующей формулы:

Для вычисления периметра вам необходимо знать длину одной стороны вписанного шестиугольника. Умножив ее на 6, вы получите значение периметра. Эта формула работает для вписанных шестиугольников любого размера.

Пример расчета периметра вписанного шестиугольника:

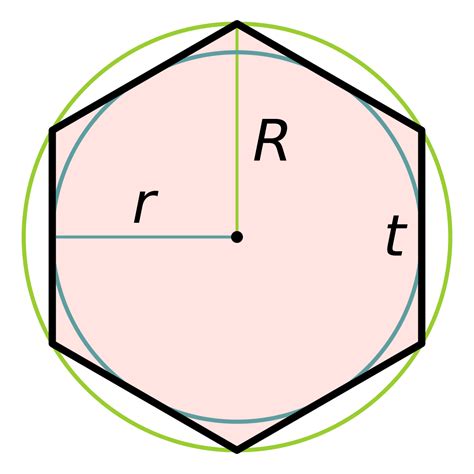
Для того чтобы найти периметр вписанного шестиугольника, нужно знать длину одной из его сторон. Возьмем в качестве примера шестиугольник, вписанный в окружность с радиусом 5 единиц.

1. Найдем длину стороны шестиугольника. Для этого воспользуемся формулой: длина_стороны = (2 * радиус * sin(π/6)).

где π равно 3.14, а sin(π/6) - синус угла 30 градусов, равный 0.5.

2. Подставим значения в формулу: длина_стороны = (2 * 5 * 0.5) = 5 единиц.

3. Умножим длину стороны на 6, так как шестиугольник имеет 6 сторон: периметр = 5 * 6 = 30 единиц.

Таким образом, периметр вписанного шестиугольника с радиусом окружности 5 единиц составляет 30 единиц.