Периметр и площадь - это два важных понятия в геометрии. Они помогают нам расчитать размеры различных фигур и объектов, а также решать разнообразные задачи. Знание способов нахождения периметра по известным длинам сторон и площади поможет вам в решении различных учебных и практических задач.
Периметр фигуры представляет собой сумму длин всех ее сторон. Для некоторых простых фигур, таких как квадрат или прямоугольник, нахождение периметра не представляет сложности - достаточно сложить длины всех сторон. Однако, при наличии сложных фигур, состоящих из кривых и изгибов, вычисление периметра может потребовать использования математических формул и теорем.
Нахождение периметра по площади и длине - это один из методов, которые могут использоваться для нахождения периметра некоторых фигур. Для этого сначала находится площадь фигуры, а затем, используя известное значение площади и длину стороны, находится периметр. Этот метод можно использовать для различных фигур, начиная от простейших, таких как квадрат и прямоугольник, до более сложных, таких как треугольник и окружность.
Почему важно знать как найти периметр по площади и длине?

Периметр - это сумма всех сторон геометрической фигуры. Зная периметр, можно определить длину каждой стороны и общую длину контура фигуры. Это особенно полезно при решении задач по черчению, строительству и архитектуре, где необходимо точно определить длины сторон и их сумму.
Площадь - это мера поверхности фигуры. Зная площадь фигуры, можно определить площадь поверхности, которую она занимает, а также провести сравнительные анализы между разными фигурами. Например, зная площадь помещения, можно рассчитать необходимое количество материалов для его отделки или выбрать наиболее оптимальную форму участка.
Навык нахождения периметра по площади и длине также помогает развить математическое мышление, логическое рассуждение и абстрактное мышление. Он требует анализа данных, использования формул и умения применять математические концепции в реальных ситуациях.
В конечном итоге, знание, как найти периметр по площади и длине, помогает нам лучше понять и взаимодействовать с окружающим миром, решать задачи и применять наши знания в практических ситуациях.
Какие формулы использовать для расчета периметра?

Расчет периметра зависит от формы фигуры. У каждой фигуры есть своя уникальная формула для определения ее периметра. Ниже приводим некоторые примеры:
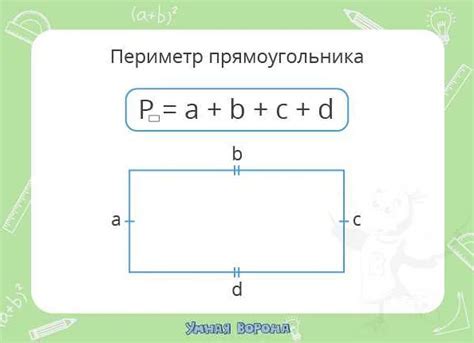
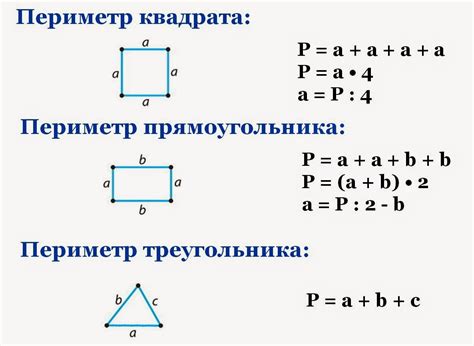
Для прямоугольника: Периметр прямоугольника можно вычислить, сложив все его стороны. Формула: P = 2 * (a + b), где a и b - длины сторон прямоугольника.
Для квадрата: Периметр квадрата можно вычислить, умножив длину одной стороны на 4. Формула: P = 4a, где a - длина стороны квадрата.
Для треугольника: Периметр треугольника можно вычислить, сложив длины всех его сторон. Формула: P = a + b + c, где a, b и c - длины сторон треугольника.
Для круга: Периметр (или длина окружности) круга можно вычислить, умножив его диаметр на число Пи (приближенно равное 3.14159). Формула: P = 2 * Пи * r, где r - радиус круга.
Помните, что для различных фигур существует множество других формул для расчета периметра. Важно всегда учитывать форму фигуры и правильно применять соответствующую формулу.
Примеры расчета периметра по площади и длине
Чтобы проиллюстрировать, как можно расчитать периметр по известной площади и длине, рассмотрим несколько примеров.
Пример 1:
Площадь прямоугольника равна 24 квадратных метра, а ширина равна 4 метра. Чтобы найти периметр, нужно рассчитать длину. Для этого мы можем использовать формулу площади прямоугольника - S = a * b, где S - площадь, а a и b - стороны прямоугольника. Подставив известные значения, получим следующее уравнение: 24 = 4 * b. Решив его, найдем длину: b = 6 метров. Зная длину и ширину прямоугольника, мы можем легко найти периметр, используя формулу периметра прямоугольника - P = 2 * (a + b). Подставив значения, получим: P = 2 * (4 + 6) = 20 метров. Таким образом, периметр прямоугольника равен 20 метрам.
Пример 2:
Допустим, у нас есть квадрат со стороной 5 сантиметров и периметром 20 сантиметров. Чтобы найти площадь, нам нужно знать длину стороны квадрата, что уже известно. Мы можем использовать формулу периметра квадрата - P = 4 * a, где P - периметр, а a - сторона квадрата. Подставив известные значения, получаем: 20 = 4 * a. Решив уравнение, находим длину стороны: a = 5 сантиметров. Зная длину стороны, можем найти площадь квадрата, используя формулу площади квадрата - S = a^2. Подставив значение, получаем: S = 5^2 = 25 квадратных сантиметров. Таким образом, площадь квадрата равна 25 квадратным сантиметрам.
Это всего лишь некоторые примеры расчета периметра по площади и длине. В реальной практике могут быть использованы и другие формулы в зависимости от геометрической фигуры. Однако, практическая работа с этими формулами позволяет легче понять и получить ответы на вопросы в области геометрии.
Советы по расчету периметра по площади и длине
Расчет периметра по площади и длине может быть полезным при решении различных задач, как в математике, так и в повседневной жизни. В данном разделе представлены несколько советов, которые могут помочь вам в этом расчете.
- Перед началом расчета обязательно проверьте единицы измерения всех величин. Убедитесь, что площадь и длина имеют одинаковую систему измерения.
- Если у вас есть формула для расчета периметра по площади или длине, убедитесь, что вы правильно применяете ее. Проверьте каждый шаг расчета и убедитесь, что вы правильно использовали все известные значения.
- Иногда бывает полезно разбить фигуру на более простые формы или линии, чтобы упростить расчет периметра. Используйте геометрические свойства фигуры, чтобы найти дополнительные значения, которые помогут вам получить точный периметр.
- Будьте внимательны при округлении ответа. Проверьте, какие требования к точности указаны в задаче и следуйте им.
- Если у вас возникли трудности или вы не уверены в правильности расчета, не стесняйтесь обратиться за помощью к специалисту или использовать онлайн-калькуляторы для периметра.
Следуя этим советам, вы сможете более точно и уверенно рассчитывать периметр по площади и длине в различных задачах.