Треугольники и окружности являются одними из основных геометрических фигур, которые мы изучаем в школе. Они встречаются во многих задачах и строительных проектах. Но что делать, если у вас есть треугольник и внутри него окружность? Как найти площадь и периметр этого треугольника? Этот вопрос вызывает некоторые сложности, которые мы попытаемся разрешить в этой статье.
Для начала, давайте рассмотрим, как найти площадь и периметр обычного треугольника. Это достаточно простая задача, которую мы обычно решаем с помощью формул Герона или полупериметра. Но, когда внутри треугольника есть окружность, все меняется. Ведь радиус окружности может влиять на размеры треугольника.
Для вычисления площади и периметра треугольника с окружностью внутри, нужно знать радиус окружности и длины его сторон. В этой статье мы рассмотрим несколько способов нахождения этих параметров в различных ситуациях. Также, мы познакомимся со свойствами таких треугольников и узнаем, как они могут быть использованы для решения задач.
Основные понятия
Для понимания алгоритма поиска площади и периметра треугольника с окружностью внутри, необходимо разобраться в следующих основных понятиях:
| Термин | Описание |
|---|---|
| Треугольник | Геометрическая фигура, образованная тремя отрезками, соединяющими три точки, не лежащие на одной прямой. |
| Окружность | Множество точек, расположенных на плоскости и равноудаленных от одной фиксированной точки, называемой центром окружности. |
| Радиус окружности | Отрезок, соединяющий центр окружности и ее любую точку. Радиус - это половина диаметра окружности. |
| Диаметр окружности | Отрезок, проходящий через центр окружности и имеющий свои концы на окружности. Диаметр - это удвоенный радиус окружности. |
| Площадь треугольника | Величина, выражающая количество плоскости, заключенной внутри треугольника. |
| Периметр треугольника | Сумма длин его сторон. Это периметр, ограничивающий треугольник. |
Основные понятия геометрии играют ключевую роль при решении задачи о поиске площади и периметра треугольника с окружностью внутри. Необходимо уяснить определения треугольника, окружности, а также понятия радиуса, диаметра, площади и периметра, чтобы приступить к решению задачи.
Формулы расчета площади треугольника
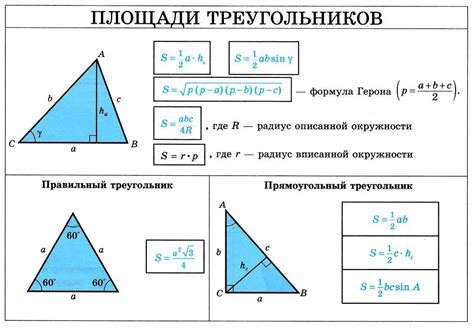
Площадь треугольника может быть рассчитана с помощью различных формул, в зависимости от того, какие данные о треугольнике известны.
1. Для треугольника, у которого известны длины всех сторон (a, b и c), можно воспользоваться формулой Герона:
S = √(p·(p - a)·(p - b)·(p - c)),
где S - площадь треугольника,
p - полупериметр треугольника (p = (a + b + c)/2),
a, b и c - длины сторон треугольника.
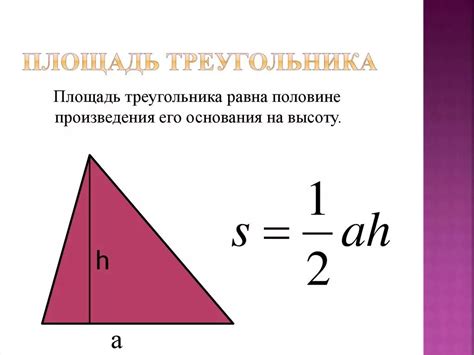
2. Если известны длина одной стороны треугольника (a) и высота, опущенная на эту сторону (h), площадь можно вычислить по формуле:
S = (1/2)·a·h,
где S - площадь треугольника,
a - длина стороны треугольника,
h - высота, опущенная на сторону a.
3. Для треугольника, у которого известны длины двух сторон (a и b) и угол между этими сторонами (α), площадь можно вычислить по формуле:
S = (1/2)·a·b·sin(α),
где S - площадь треугольника,
a и b - длины сторон треугольника,
α - угол, заключенный между сторонами a и b.
Эти формулы позволяют рассчитать площадь треугольника при разных условиях, что полезно при решении различных геометрических задач.
Формулы расчета периметра треугольника

Если заданы длины сторон треугольника a, b и c, то периметр P вычисляется по формуле:
P = a + b + c
Если известны координаты вершин треугольника - (x1, y1), (x2, y2) и (x3, y3), то длины его сторон можно вычислить с помощью формулы расстояния между двумя точками:
a = √((x2 - x1)^2 + (y2 - y1)^2)
b = √((x3 - x2)^2 + (y3 - y2)^2)
c = √((x1 - x3)^2 + (y1 - y3)^2)
Затем периметр P вычисляется по формуле:
P = a + b + c
Если известны длины сторон треугольника a, b и c, а также его углы α, β и γ, то периметр P можно вычислить с помощью формулы синусов:
P = a + b + c = 2R(sinα + sinβ + sinγ)
где R - радиус описанной окружности треугольника.
Треугольник с окружностью внутри

Окружность, вписанная в треугольник, касается каждой стороны треугольника в одной точке. Эти точки касания называются точками контакта. Линия, соединяющая точки контакта, называется линией соприкосновения.
Треугольник с окружностью внутри имеет две важные характеристики: площадь и периметр. Площадь треугольника с окружностью внутри можно найти, используя формулу S = r * (p - a) * (p - b) * (p - c), где r - радиус окружности, p - полупериметр треугольника, a, b, c - стороны треугольника.
Периметр треугольника с окружностью внутри можно найти, используя формулу P = a + b + c, где a, b, c - стороны треугольника.
Таким образом, треугольник с окружностью внутри представляет собой интересный объект геометрии, который имеет определенные характеристики, такие как площадь и периметр, которые могут быть вычислены с использованием специальных формул.
Формулы расчета площади треугольника с окружностью внутри
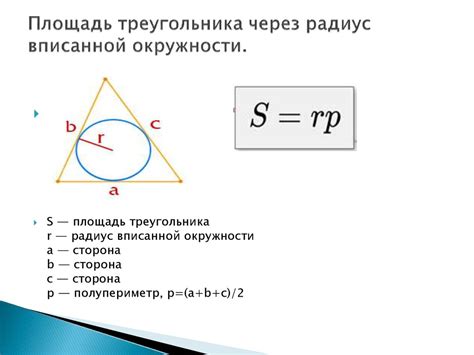
Если в треугольнике имеется окружность, то можно использовать следующие формулы для расчета площади:
- Площадь треугольника, образованного сторонами треугольника и хордой окружности, может быть вычислена по формуле:
S = (r * a) / 2
где S - площадь треугольника, r - радиус окружности, a - длина хорды. - Если известны радиус окружности r и длины сторон треугольника a, b, c, то площадь треугольника может быть вычислена по формуле Герона:
S = sqrt(p * (p - a) * (p - b) * (p - c))
где S - площадь треугольника, p - полупериметр треугольника (p = (a + b + c) / 2).
Обрати внимание, что в первой формуле хорда окружности должна быть линией, соединяющей вершины треугольника и касательную окружности.
Формулы расчета периметра треугольника с окружностью внутри
Формулы для расчета периметра треугольника с окружностью внутри основаны на свойствах такого треугольника. Для удобства рассмотрим случай равностороннего треугольника.
Пусть сторона равностороннего треугольника равна a, а радиус вписанной в него окружности равен r.
Периметр треугольника можно рассчитать с помощью следующей формулы:
P = 3a
Так как треугольник равносторонний, все его стороны имеют одинаковую длину a.
Также можно использовать формулу:
P = 6r
Формула основана на том факте, что радиус окружности, вписанной в треугольник, равен половине высоты этого треугольника.
Обратите внимание, что эти формулы применимы только для равностороннего треугольника с вписанной окружностью.