Круг - одна из самых простых и известных геометрических фигур. Уже с детства мы знаем, что круг имеет форму замкнутой кривой линии, все точки которой равноудалены от одной точки - центра.
Одно из основных свойств круга - его площадь. Хотя мы часто слышим о площади круга, не всегда понимаем, как она вычисляется. В этой статье мы рассмотрим формулу для вычисления площади круга и познакомимся с числом π, которое является неотъемлемой частью этой формулы.
Для вычисления площади круга используется так называемая формула площади круга, которая выглядит следующим образом: S = π * r2, где S обозначает площадь, π (пи) - математическая константа, а r - радиус круга, то есть растояние от центра круга до любой точки на его окружности.
Что такое круг и как вычислить его площадь?
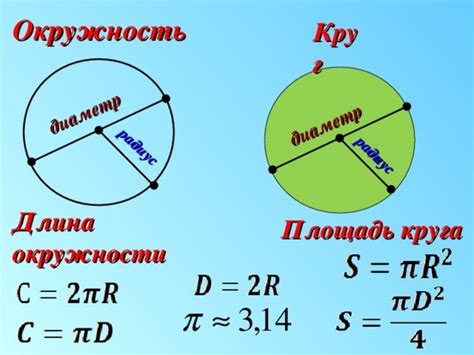
Вычисление площади круга осуществляется с использованием формулы: S = π * r^2, где S - площадь круга, π (пи) - математическая константа, которая приближенно равна 3,14, а r - радиус круга.
Чтобы вычислить площадь круга, нужно сначала измерить радиус, а затем воспользоваться формулой.
В таблице ниже представлены примеры вычисления площади круга для различных значений радиуса:
| Радиус (r) | Площадь (S) |
|---|---|
| 2 | 12.57 |
| 5 | 78.54 |
| 10 | 314.16 |
Таким образом, площадь круга можно вычислить, зная его радиус и используя формулу S = π * r^2. Эта формула широко применяется в различных областях науки, техники и повседневной жизни.
Определение круга и его особенности
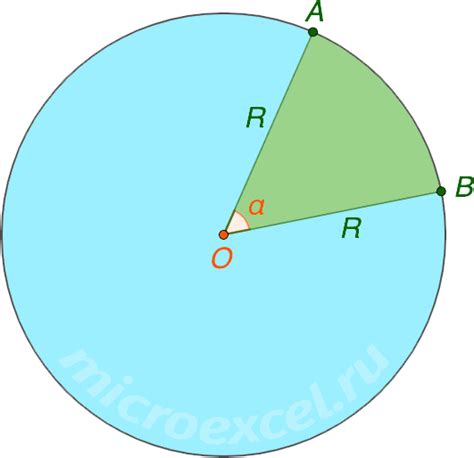
Основной параметр, используемый для описания круга, – радиус. Радиус – это расстояние от центра круга до любой его точки. Другой параметр, связанный с кругом, – диаметр, который является удвоенным значением радиуса.
Круг имеет несколько особенностей, которые делают его уникальным:
| Площадь круга | Формула для вычисления площади круга: S = πr^2, где S – площадь, π – число пи (примерное значение 3,14159), r – радиус. Площадь круга равна площади кругового сектора и кругового сегмента. |
| Длина окружности | Формула для вычисления длины окружности: C = 2πr, где C – длина окружности, π – число пи (примерное значение 3,14159), r – радиус. |
| Число π | Число π является иррациональным числом, то есть его десятичное представление не имеет конечное количество цифр после запятой и не повторяется периодически. При аппроксимации число π часто округляют до 3,14159 или 3,14. |
Из-за своих особенностей, круг широко применяется в различных областях, таких как инженерия, архитектура, физика, математика и технологии.
Расчет площади круга с помощью формулы
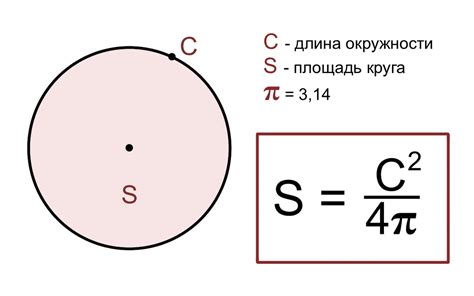
Площадь круга может быть рассчитана с использованием формулы, которая основана на радиусе круга и числе π (пи).
Формула для расчета площади круга:
S = π * r^2
Где:
- S - площадь круга
- π - число π (пи) ≈ 3.14159
- r - радиус круга
Для рассчета площади круга нужно знать его радиус. Радиус - это расстояние от центра круга до любой точки на окружности.
Чтобы найти площадь круга, нужно возвести радиус в квадрат и умножить его на число π.
Например, если задан радиус круга r = 5, то площадь круга можно рассчитать следующим образом:
S = 3.14159 * 5^2 = 3.14159 * 25 ≈ 78.53975
Таким образом, площадь круга с радиусом 5 составляет примерно 78.53975 единицы площади.
Используя данную формулу, можно рассчитать площадь круга для любого значения радиуса.
Окружность и радиус круга: важные понятия
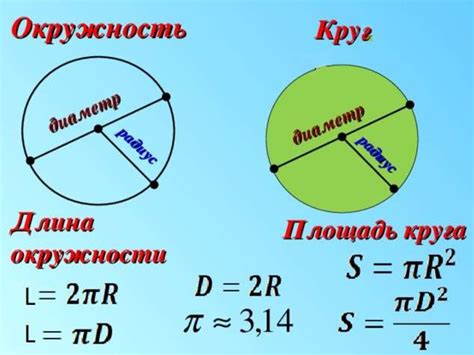
Радиус круга - это отрезок, соединяющий центр окружности с любой точкой на ее окружности. Радиус является не только длиной этого отрезка, но и одним из важных параметров, определяющих свойства окружности.
Окружность и радиус круга в тесной взаимосвязи определяют понятие площади круга. Площадь круга вычисляется по формуле S = π * r^2, где S - площадь круга, π - число пи (3,14), r - радиус круга.
Радиус круга также играет важную роль в формулах для вычисления длины окружности и дуги окружности. Длина окружности вычисляется по формуле L = 2 * π * r, где L - длина окружности, r - радиус круга. А длина дуги окружности вычисляется по формуле L = α * r, где L - длина дуги окружности, α - центральный угол, измеряемый в радианах, r - радиус круга.
Понимание концепции окружности и радиуса круга является фундаментальным для изучения геометрии и тесно связано с практическими применениями в различных областях, таких как строительство, инженерия и наука.
Интересные факты о числе π

1. День числа π отмечается 14 марта (3/14) в память о рождении английского ученого-физика Сэра Уильяма Гамильтона, который внес величайший вклад в развитие теории чисел и геометрии.
2. Число π является иррациональным, что означает, что его десятичное представление не может быть выражено точным конечным числом или периодической десятичной дробью.
3. Последовательность чисел после десятичной точки в числе π не имеет повторяющихся групп чисел. Исследователи пробовали применять различные алгоритмы для нахождения какой-либо закономерности в этой последовательности, но пока безуспешно.
4. Максимальное известное количество знаков числа π составляет более 31,4 триллиона десятичных разрядов. Для его вычисления требовалось около 121 дня на суперкомпьютере.
5. Число π часто используется в различных науках и технологиях, включая физику, математику, инженерию и компьютерные науки. Оно применяется, например, для расчета площади и объема круга, а также в формулах для нахождения периметра и длины дуги.
| Приближенное значение π | Значение | Дата |
|---|---|---|
| 3,14 | Архимед | около 250 г. до н.э. |
| 3,14159 | Лидский папирус | около 1650 г. |
| 3,14159265358979323846 | Value of π by Yasumasa Kanada | 1999 г. |
Применение числа π в вычислении площади круга

Площадь круга можно вычислить с помощью формулы S = πr², где S - площадь, π - число π и r - радиус круга. Радиус круга представляет собой расстояние от его центра до любой точки на его окружности.
Применение числа π в вычислении площади круга позволяет получить точное значение этой физической величины. Так как число π является иррациональным числом, его десятичные разряды не повторяются и имеют бесконечную длину. Однако для практических рассчетов достаточно использовать его приближенное значение, округленное до нескольких знаков после запятой.
Например, если радиус круга равен 5 см, то его площадь будет равна π * 5² = 3,14159 * 25 ≈ 78,53975 см². Таким образом, применение числа π в формуле позволяет вычислить площадь круга, используя только радиус.
Знание формулы площади круга и применение числа π являются основой для решения различных задач в геометрии, физике, инженерии и других областях науки и техники, где требуется вычисление площади кругового объекта.
Роль π в геометрии и математике

Длина окружности можно вычислить с использованием формулы, где π является неотъемлемой частью этого расчета. А еще π используется для вычисления площади круга, где радиус этого круга также является обязательной составляющей формулы.
Пи также играет важную роль в таких областях математики, как тригонометрия и аналитическая геометрия. Оно присутствует во многих математических уравнениях и формулах, и его значение точно определено и известно миллионам математиков и учеников по всему миру.
Значение числа π бесконечно и не может быть представлено в виде обыкновенной или десятичной дроби. Однако оно является иррациональным числом, что означает, что его можно приблизить до определенной точности с помощью десятичной записи или бесконечных десятичных разложений.
Изучение и понимание роли числа π в геометрии и математике играет важную роль в развитии математической науки и приложений этой науки в других областях знаний.
Пи (π) - это не просто математическая константа, она является ключом к пониманию и использованию множества геометрических и математических концепций и формул.
Знание и понимание π открывают перед нами много новых возможностей и позволяют решать разнообразные задачи в геометрии и математике.
История открытия числа π

История открытия числа π начинается еще в Древнем Египте и Древней Греции. Уже в этих цивилизациях было замечено, что отношение длины окружности к ее диаметру является постоянным для всех окружностей. Оно было обозначено буквой π, и его приближенное значение было вычислено с использованием геометрических методов.
В течение многих столетий математики стремились точно определить значение числа π. Это привело к созданию различных методов и алгоритмов для его вычисления. Однако, числа π оставалось иррациональным, что означает, что его десятичное представление не имеет конечного числа цифр после запятой и не повторяется.
В XIX веке немецкий математик Фердинанд фон Линдеманн доказал, что число π трансцендентно, что означает, что оно не является корнем никакого алгебраического уравнения с рациональными коэффициентами. Это было огромным достижением в математике и окончательно разрешило вопрос о невозможности точного выражения значения π через рациональные числа или корни.
С появлением компьютерной технологии и различных численных методов вычисления, удалось вычислить число π с удивительной точностью. Сейчас мы знаем более 31 трлн десятичных знаков числа π и продолжаем вычислять еще больше. Но, несмотря на все эти вычисления, число π остается загадкой и объектом внимания для математиков по всему миру.
Значение числа π в различных задачах и областях
Число π широко используется в различных математических и научных задачах, а также в различных областях, таких как:
| Область применения | Примеры |
|---|---|
| Геометрия | Формула для вычисления площади круга: S = πr² |
| Тригонометрия | Соотношение между радианами и градусами: 180° = π радианов |
| Физика | Формула для вычисления длины окружности: C = 2πr |
| Статистика | Использование в формуле для вычисления дисперсии и среднего квадратического отклонения |
| Инженерия | Калькуляция для точного определения величин в инженерных расчетах |
| Алгоритмы и вычисления | Использование в алгоритмах численного интегрирования и симуляциях |
Значение числа π имеет важное значение в многих областях, позволяя совершать точные расчеты и вычисления. Вся его многообразная применимость подчеркивает фундаментальную роль этой константы в математике и науке в целом.