Площадь геометрических фигур - одна из основных тем, изучаемых в школе, и в 9 классе ученики сталкиваются с задачами, требующими нахождения площади неровных фигур по клеточкам. Для решения таких задач необходимо использовать навыки работы с графическими моделями и определение площади за счет подсчета клеточек.
Подсчет площади неровной фигуры по клеточкам может показаться сложным ом, но, на самом деле, этот процесс становится проще с определенной методикой. Один из способов подсчета площади – разбить фигуру на прямоугольники и прямоугольные треугольники, а затем сложить площади этих фигур. Другой способ – подсчет площади путем отметки клеточек, находящихся внутри фигуры, и подсчета их количества.
Необходимая информация для нахождения площади неровной фигуры может быть предоставлена в задаче или быть загадкой, и ученику придется провести дополнительные измерения или выполнить несколько шагов для получения нужных сведений. Процесс нахождения площади по клеточкам требует внимательности и аккуратности, и помогает ученикам развить логическое мышление и уверенность в решении геометрических задач.
Важность понимания клеточной геометрии

Клеточная геометрия широко используется в различных областях, таких как архитектура, дизайн, графика и техническое черчение. Понимание клеточной структуры позволяет точно измерять и располагать объекты, а также строить сложные фигуры.
Понимание клеточной геометрии также помогает учащимся развивать свои навыки визуального анализа и пространственного мышления. Они могут видеть и понимать отношения между элементами фигур и оценивать их размеры и площади.
Кроме того, знание клеточной геометрии важно для практического применения математических знаний в повседневной жизни. Умение рассчитывать площадь фигур, изображенных на клеточной сетке, поможет учащимся в решении задач по мебельному дизайну, планированию помещений или укладке плитки.
Ключевая роль в учебном процессе

Поиск площади неровных фигур по клеточкам требует применения различных методов и стратегий. Ученики должны уметь разбить фигуру на более простые геометрические фигуры, такие как прямоугольники, треугольники или трапеции. Затем они могут использовать известные формулы для расчета площади этих более простых фигур и сложить их, чтобы получить общую площадь.
Эта тема также помогает ученикам понять важность точности в математике. Они должны быть внимательны при подсчете клеточек, чтобы не допустить ошибок. В случае иной формы фигуры, которую нельзя разделить на простые геометрические фигуры, учащиеся должны использовать приближенные методы, такие как подсчет клеток внутри фигуры или использование графических инструментов.
Кроме того, работа с площадью неровных фигур по клеточкам способствует развитию математической интуиции у учащихся. Они могут развить способность видеть общие закономерности и регулярности, а также умение анализировать сложные геометрические фигуры.
Таким образом, расчет площади неровной фигуры по клеточкам играет ключевую роль в учебном процессе, развивая у учащихся различные навыки и способности. Это важная тема, которая помогает студентам развить геометрическое мышление и улучшить понимание математики в целом.
Определение площади неровной фигуры

Для определения площади неровной фигуры необходимо разбить ее на более простые геометрические фигуры, такие как квадраты или прямоугольники и сложить площади этих составных частей. Например, если неровная фигура состоит из квадратов, то нужно сложить площади всех квадратов, образующих данную фигуру.
Разбиение неровной фигуры на составные части и определение их площадей может быть довольно сложной задачей. Для упрощения этого процесса, можно использовать клеточную сетку, размещая неровную фигуру на клеточках и подсчитывая количество клеточек, занимаемых каждой составной частью фигуры. Площадь неровной фигуры в этом случае будет равна сумме площадей всех составных частей.
Важно помнить, что площадь неровной фигуры измеряется в квадратных единицах площади, таких как квадратные сантиметры (см²) или квадратные метры (м²). Правильно выполненные расчеты позволяют точно определить площадь неровной фигуры и использовать эту информацию для решения различных задач в геометрии и практических ситуациях.
Точки и клетки как основа расчетов
Расчет площади неровной фигуры на клеточной сетке производится путем подсчета количества клеток, охватывающих данную фигуру. Для этого необходимо определить границы фигуры и подсчитать количество клеток, которые она занимает.
Важно отметить, что при расчете площади учитываются как полностью охваченные клетки, так и частично пересекаемые клетки. Если фигура проходит по границе клетки без пересечения ее внутренней части, данная клетка также считается охваченной фигурой.
Для удобства подсчета площади, можно помечать или закрашивать охваченные клетки, чтобы не потерять их при переключении с одного участка фигуры на другой. Помеченные клетки помогут визуально определить границы и форму фигуры.
Использование точек и клеток как основы расчетов позволяет точно и систематически оценить площадь неровной фигуры на клеточной сетке. Такой подход важен при выполнении задач из геометрии и математики, а также в реальных ситуациях, связанных с измерением площади на плоскости.
Шаги для нахождения площади
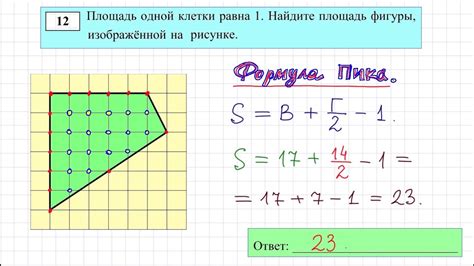
Для нахождения площади неровной фигуры по клеточкам в 9 классе, следуйте следующим шагам:
- Визуализируйте заданную фигуру на клеточной сетке, где каждая клеточка представляет одинаковую площадь.
- Проследите за контуром фигуры и определите, сколько целых клеточек находится внутри этого контура.
- Посчитайте количество полузаполненных клеточек, которые пересекают контур фигуры. Например, если половина клеточки находится внутри фигуры, а другая половина наружу, такая клеточка считается полузаполненной.
- Подсчитайте количество полных и полузаполненных клеточек и запишите эти числа.
- Умножьте количество полных клеточек на площадь одной клеточки, обозначаемую символом "S". Запишите полученное число как S1.
- Умножьте количество полузаполненных клеточек на половину площади одной клеточки и запишите полученное число как S2.
- Найдите сумму S1 и S2 для получения общей площади фигуры.
Теперь вы знакомы с шагами, которые помогут вам находить площадь неровной фигуры по клеточкам в 9 классе.
Подход к измерению на основе формулы

Для нахождения площади неровной фигуры по клеточкам в 9 классе можно использовать подход на основе формулы. Это позволяет точно измерить площадь и получить более точные результаты.
Шаги для измерения площади с использованием формулы:
- Визуализируйте фигуру и клеточку графика на листе бумаги или в редакторе графики.
- Приблизительно определите количество клеточек, занимаемых фигурой.
- Измерьте длину и ширину одной клеточки в выбранной системе единиц (например, миллиметрах или сантиметрах).
- Просуммируйте количество клеточек, занимаемых фигурой, и умножьте на площадь одной клеточки.
- Результат выражается в выбранной единице измерения и является приближенной площадью фигуры.
Формула для нахождения площади неровной фигуры по клеточкам будет иметь вид:
Площадь = количество клеточек × площадь одной клеточки
Важно учесть, что этот метод дает приближенные значения, особенно при сложных и неровных фигурах. Для точных измерений рекомендуется использовать более сложные методы, такие как интегрирование или аналитическая геометрия.
Примеры задач и применение знаний

На уроке математики 9 класса ученикам обычно предлагается решить задачи на нахождение площади неровных фигур по клеточкам. Знания, полученные в предыдущих уроках о нахождении площади прямоугольников и треугольников, могут быть применены при решении этих задач.
Пример задачи:
На клетчатом поле задана следующая фигура:
Необходимо найти площадь этой фигуры.
Для решения задачи нужно:
- Разделить фигуру на прямоугольники и треугольники.
- Найти площадь каждой фигуры.
- Сложить площади всех фигур, чтобы получить искомую площадь.
Применение знаний о нахождении площади неровных фигур по клеточкам может быть полезно при решении практических задач, например, при расчете площади поля для посадки растений или при определении площади недвижимости на кадастровой карте.