Призма треугольной формы - это геометрическое тело, которое имеет две параллельные плоскости, называемые основаниями, и боковые стороны, состоящие из треугольных граней. Основание призмы треугольной формы - это треугольная плоскость, которая образует нижнюю или верхнюю границу призмы.
Для вычисления площади основания призмы треугольной формы необходимо знать значение хотя бы одной измеренной стороны треугольника, а также уметь использовать специальные формулы. Это позволит нам получить точное значение площади основания призмы для различных треугольников, включая равносторонние и разносторонние треугольники.
Формула для вычисления площади основания призмы треугольной формы:
S = (a * h) / 2,
где S - площадь основания призмы, a - длина одной измеренной стороны треугольника, h - высота основания призмы.
Используя эту формулу, вы сможете без труда вычислить площадь основания призмы треугольной формы и использовать это значение в дальнейших математических расчетах или практических задачах.
Определение площади основания призмы треугольной
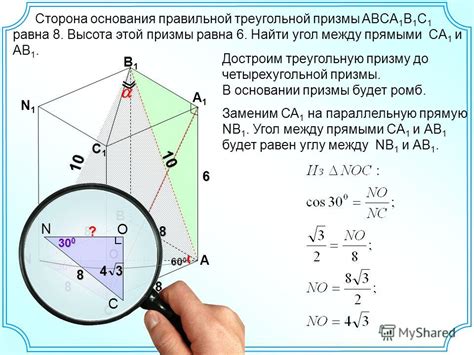
Формула для нахождения площади треугольника:
S = 0.5 * a * b * sin(angle), где S – площадь треугольника, a и b – длины двух сторон треугольника, angle – угол между этими сторонами.
Площадь основания призмы треугольной равна площади треугольника, поэтому применяется та же формула.
Пример нахождения площади основания призмы треугольной:
Пусть треугольник имеет стороны длиной 4 см, 5 см и угол между ними равен 60 градусам.
Подставим значения в формулу:
S = 0.5 * 4 см * 5 см * sin(60 градусов)
Вычислим:
S = 0.5 * 4 см * 5 см * 0.866
S ≈ 3.464 см²
Таким образом, площадь основания призмы треугольной равна примерно 3.464 см².
Что такое призма треугольная?

Основания призмы треугольной являются треугольниками, а боковые грани – прямоугольными параллелограммами. Таким образом, призма треугольная имеет три боковые грани и два треугольных основания. Общая характеристика всех призм треугольной формы – это треугольник в качестве основания и выпуклая форма.
Призмы треугольной формы можно найти в различных объектах и конструкциях. Они широко используются в архитектуре, рисунках, моделировании и других областях. Знание о форме и свойствах призмы треугольной помогает в решении задач с расчетами площади основания и объема этого геометрического тела.
Как найти длину стороны треугольника основания?

Для того чтобы найти длину каждой стороны треугольника, составляющего основание призмы треугольной формы, можно использовать различные методы.
Один из самых простых и точных способов - использование теоремы Пифагора. Если известны длины двух сторон треугольника, можно найти длину третьей стороны, применяя следующую формулу:
| Формула теоремы Пифагора: |
|---|
| a2 + b2 = c2 |
Где a и b - длины известных сторон, а c - длина неизвестной стороны треугольника.
Если известны длины всех сторон треугольника, можно использовать формулу Герона для нахождения его площади:
| Формула Герона: |
|---|
| S = √(p(p - a)(p - b)(p - c)) |
Где S - площадь треугольника, a, b и c - длины его сторон, и p - полупериметр, вычисляемый следующим образом:
| Формула полупериметра: |
|---|
| p = (a + b + c) / 2 |
Используя эти формулы, можно легко и точно рассчитать длину и площадь треугольника, составляющего основание призмы треугольной формы.
Как найти высоту призмы треугольной?
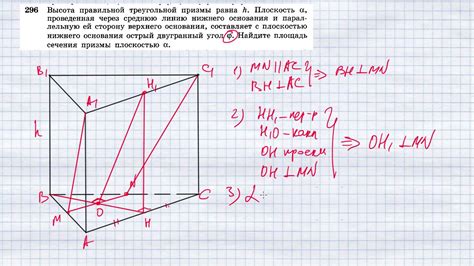
Если вам известны длины сторон треугольника основания и его высота, то высоту призмы треугольной можно найти по формуле:
Высота = (2 * Периметр треугольника основания * Высота треугольника основания) / (3 * Длина стороны треугольника основания)
Если вам известны площадь основания и объем призмы треугольной, то высоту можно найти по формуле:
Высота = Объем призмы треугольной / Площадь основания
Если же вам известны вершина призмы, ее высота от основания и площадь основания, то высоту можно найти, применив теорему Пифагора:
Высота = √(Высота призмы^2 - (1/4) * Длина стороны треугольника основания^2)
Не забывайте, что единицы измерения должны быть одинаковыми для всех величин в формуле.
Как найти площадь основания?
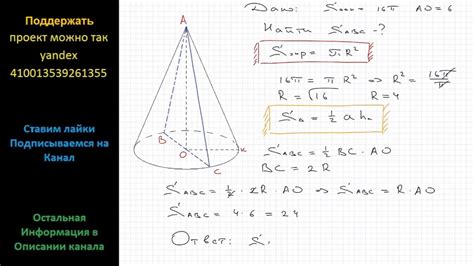
Площадь основания призмы треугольной можно найти с помощью формулы, учитывающей тип основания и данные, доступные о нем.
1) Если известна длина стороны треугольника, можно найти площадь основания с помощью формулы площади треугольника:
S = (a * h) / 2,
где S - площадь треугольника, a - длина стороны треугольника, h - высота падающая на сторону треугольника.
2) Если известны длины всех сторон треугольника, можно воспользоваться формулой Герона:
S = sqrt(p * (p - a) * (p - b) * (p - c)),
где S - площадь треугольника, p - полупериметр треугольника, a, b, c - длины сторон треугольника.
3) Если известны координаты вершин треугольника в трехмерном пространстве, можно найти площадь основания призмы, используя формулу площади треугольника по координатам вершин:
S = |(x2 - x1) * (y3 - y1) - (x3 - x1) * (y2 - y1)| / 2,
где S - площадь треугольника, (x1, y1), (x2, y2) и (x3, y3) - координаты вершин треугольника.
Учитывая тип основания и имеющиеся данные о треугольнике, можно выбрать подходящую формулу и вычислить площадь основания призмы треугольной.
Как найти площадь боковой поверхности призмы треугольной?

Площадь боковой поверхности призмы треугольной можно найти путем вычисления суммы площадей всех ее боковых граней. Для этого необходимо знать длину боковой стороны призмы и ее высоту.
Шаги для вычисления:
- Найдите площадь одного бокового треугольника. Для этого умножьте длину боковой стороны на высоту и разделите полученное значение на 2.
- Умножьте площадь одного бокового треугольника на количество боковых граней призмы.
Формула для нахождения площади боковой поверхности призмы треугольной:
Площадь боковой поверхности = площадь одного бокового треугольника * количество боковых граней
Пример:
Допустим, у вас есть треугольная призма с боковой стороной длиной 5 см и высотой 8 см. В этом случае, для нахождения площади боковой поверхности призмы нужно:
1. Найти площадь одного бокового треугольника:
Площадь = (5 см * 8 см) / 2 = 20 см²
2. Умножить площадь одного бокового треугольника на количество боковых граней (3):
Площадь боковой поверхности = 20 см² * 3 = 60 см²
Таким образом, площадь боковой поверхности треугольной призмы равна 60 см².
Как найти полную площадь призмы треугольной?
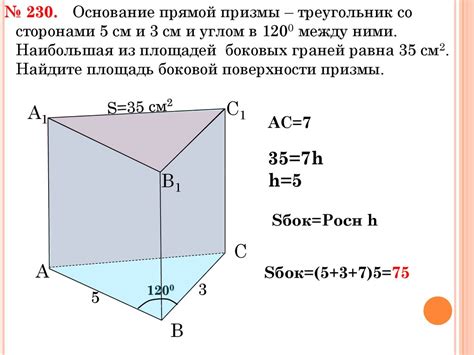
S = Sоснования + 2Sбоковой грани,
где S - полная площадь призмы, Sоснования - площадь основания призмы, Sбоковой грани - площадь боковой грани призмы.
Для расчета площади основания треугольной призмы, используется формула площади треугольника: Sоснования = (a * h) / 2, где a - длина основания треугольника, h - высота треугольника.
Площадь боковой грани призмы может быть найдена с помощью формулы площади прямоугольного треугольника: Sбоковой грани = (a * b) / 2, где a и b - катеты прямоугольного треугольника, а с гипотенузой является высота призмы.
Сложив площади основания и боковой грани призмы, мы найдем полную площадь треугольной призмы. Подставив известные значения в формулы, можно получить конкретное численное значение полной площади.
| Параметр | Формула |
|---|---|
| Площадь основания | Sоснования = (a * h) / 2 |
| Площадь боковой грани | Sбоковой грани = (a * b) / 2 |