Шар – это геометрическое тело, состоящее из всех точек пространства, равноудаленных от центра. Он обладает множеством физических и математических свойств, включая площадь поверхности. Как найти площадь поверхности шара, исходя из площади сечения? Данное руководство предоставит вам информацию о формуле для расчета этой площади, а также приведет несколько примеров для лучшего понимания.
Площадь поверхности шара – это сумма всех площадей, принадлежащих шару. Расчет площади поверхности шара может осуществляться разными способами, в зависимости от известной информации. Если у вас имеется площадь сечения шара, то вы можете использовать следующую формулу для нахождения площади поверхности шара: S = 4 * π * r², где S – площадь поверхности шара, π – число пи (примерно равное 3,14), r – радиус шара.
Давайте рассмотрим пример для лучшего понимания. Предположим, что у нас есть шар с площадью сечения, равной 9 квадратным сантиметрам. Мы хотим найти площадь поверхности этого шара. В первую очередь, нам необходимо найти радиус шара. Для этого мы можем использовать известную формулу площади сечения шара, выразив радиус через нее: r = √(S / (π * 4)), где √ - корень квадратный. Подставив известные значения, мы получим: r = √(9 / (3,14 * 4)) ≈ 0,95 сантиметра. Теперь мы можем легко найти площадь поверхности шара, заменив значения в формуле: S = 4 * 3,14 * (0,95)² ≈ 11,3 квадратных сантиметра. Таким образом, площадь поверхности шара составляет приблизительно 11,3 квадратных сантиметра.
Что такое площадь поверхности шара?
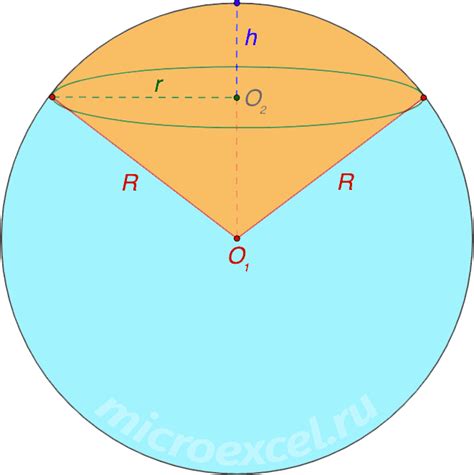
Площадь поверхности шара можно вычислить по формуле S = 4πr², где S - площадь поверхности шара, а r - радиус шара.
Для вычисления площади поверхности шара необходимо знать его радиус. Радиус это расстояние от центра шара до любой точки его поверхности.
Важно отметить, что площадь поверхности шара не включает в себя объем шара. Объем шара рассчитывается по формуле V = (4/3)πr³, где V - объем шара.
Для лучшего понимания концепции площади поверхности шара можно рассмотреть пример: если у нас есть шар с радиусом 5 см, то для вычисления его площади поверхности мы подставляем значение радиуса в формулу: S = 4π(5)² = 4π(25) ≈ 314.16 см². Таким образом, площадь поверхности шара равна примерно 314.16 квадратных сантиметров.
Итак, площадь поверхности шара является важной характеристикой этой геометрической фигуры, которая позволяет определить общую площадь его поверхности и использовать эту информацию в различных математических и научных расчетах.
Значение площади поверхности шара в математике
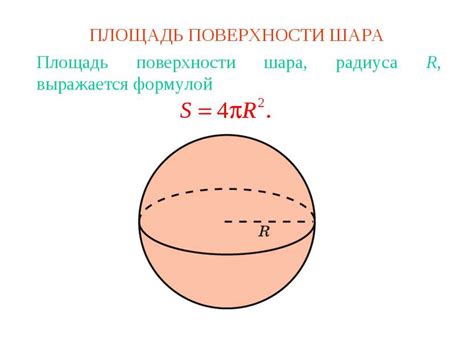
Площадь поверхности шара вычисляется с использованием формулы, в которой используется радиус шара и значение числа Пи.
Полученная площадь поверхности шара позволяет определить, сколько площади занимает его поверхность в единицах измерения.
Площадь поверхности шара является полезным понятием в различных областях науки и техники. Например, она может быть применена при расчете объемов и площадей шаровидных объектов, а также в архитектуре и дизайне для определения размеров сферических форм.
Как вычислить площадь поверхности шара?

Площадь поверхности шара можно вычислить с помощью формулы:
П = 4πr²
Где:
- П - площадь поверхности шара;
- π - математическая константа, приближенное значение которой равно 3,14159;
- r - радиус шара.
Для вычисления площади поверхности шара необходимо знать радиус данной фигуры. Если радиус неизвестен, его можно вычислить, зная диаметр шара.
Пример:
| Диаметр шара (см) | Радиус шара (см) | Площадь поверхности шара (см²) |
|---|---|---|
| 10 | 5 | 314.16 |
| 15 | 7.5 | 706.86 |
| 20 | 10 | 1256.64 |
Таким образом, для вычисления площади поверхности шара необходимо знать его радиус и использовать формулу П = 4πr².
Формула для вычисления площади поверхности шара
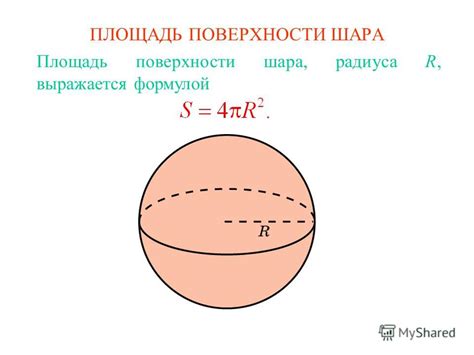
S = 4πR2
- S - площадь поверхности шара;
- π - математическая константа «пи», приближенно равная 3,14159;
- R - радиус шара.
Для примера, давайте рассмотрим шар с радиусом 5 сантиметров:
S = 4π(52) = 4π(25) = 100π ≈ 314,16 см2
Таким образом, площадь поверхности шара с радиусом 5 сантиметров приближенно равна 314,16 см2.
Примеры вычисления площади поверхности шара
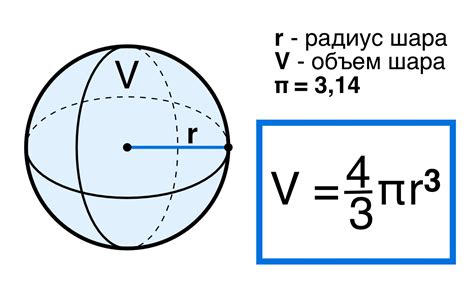
Чтобы найти площадь поверхности шара, нужно знать его радиус.
Пример 1:
| Радиус (r) | Площадь поверхности шара (S) |
|---|---|
| 1 см | 4π см² |
| 2 см | 16π см² |
| 3 см | 36π см² |
Пример 2:
| Радиус (r) | Площадь поверхности шара (S) |
|---|---|
| 0.5 м | π м² |
| 1 м | 4π м² |
| 1.5 м | 9π м² |
Пример 3:
| Радиус (r) | Площадь поверхности шара (S) |
|---|---|
| 2 ft | 16π ft² |
| 3 ft | 36π ft² |
| 4 ft | 64π ft² |
Пример 1: Вычисление площади поверхности шара с известным радиусом
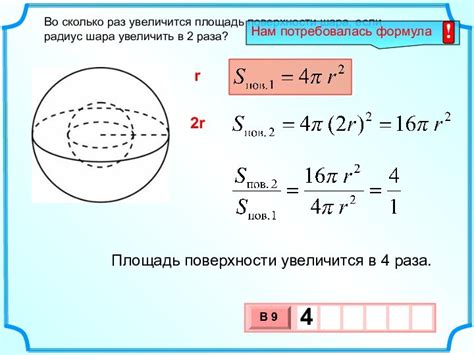
Для вычисления площади поверхности шара с известным радиусом необходимо использовать формулу:
S = 4πr²
Где:
- S - площадь поверхности шара
- π - математическая константа «пи», приближенно равная 3,14
- r - радиус шара
Например, если радиус шара равен 5 единицам длины, то для вычисления площади поверхности шара:
S = 4π(5)² = 4π(25) ≈ 314,16
Таким образом, площадь поверхности шара с радиусом 5 единиц длины составляет около 314,16 квадратных единиц.