Прямоугольные треугольники - это геометрические фигуры, которые имеют один угол равным 90 градусам. Они широко применяются в различных областях, таких как строительство, архитектура и геодезия. Найти площадь прямоугольного треугольника может понадобиться во многих ситуациях, например, при расчете площади участка земли или площади крыши здания.
Площадь прямоугольного треугольника можно найти с помощью различных способов, одним из которых является использование высоты треугольника. Высота треугольника - это отрезок, соединяющий вершину прямого угла треугольника с противоположной стороной. Зная высоту треугольника, мы можем легко найти площадь этой фигуры.
Формула для нахождения площади прямоугольного треугольника по высоте:
Площадь треугольника = (Основание * Высота) / 2
В данной формуле, основание треугольника - это одна из его сторон, а высота - расстояние от основания до вершины прямого угла.
Определение прямоугольного треугольника

Прямоугольный треугольник имеет три стороны: две катета и гипотенузу. Гипотенуза – это наибольшая сторона, которая расположена против прямого угла. Катеты – это остальные две стороны треугольника.
В прямоугольном треугольнике существует теорема Пифагора, которая позволяет находить значения сторон и высоты треугольника. Согласно этой теореме, квадрат гипотенузы равен сумме квадратов катетов.
Прямоугольные треугольники широко используются в геометрии и физике для решения различных задач. Например, высота прямоугольного треугольника, опущенная на гипотенузу, делит его на два подобных прямоугольных треугольника.
Найти площадь прямоугольного треугольника можно с помощью базовой формулы: S = (a * b) / 2, где а и b – длины катетов треугольника.
Формула для нахождения площади прямоугольного треугольника
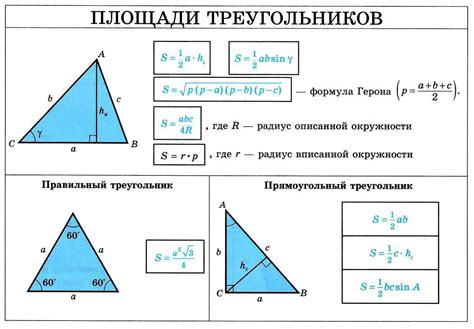
Формула:
| Площадь | = | Основание × Высота | / 2 |
Где:
- Основание - это длина одной из сторон прямоугольного треугольника, перпендикулярной к гипотенузе.
- Высота - это расстояние от противолежащего угла до основания, опущенное перпендикулярно.
Данная формула позволяет легко вычислить площадь прямоугольного треугольника при известных значениях основания и высоты.
Вычисление площади прямоугольного треугольника с помощью высоты
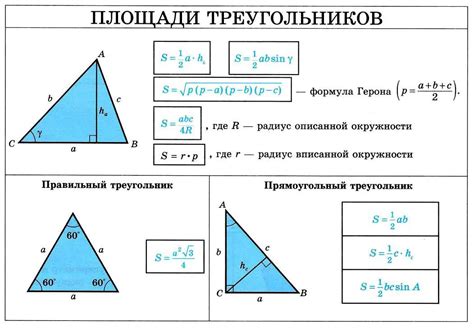
Для начала необходимо определить одну из сторон треугольника, которая называется основанием. Далее нужно измерить высоту, которая проводится из вершины прямого угла к основанию. Именно эта высота будет использована для вычисления площади треугольника.
Формула для вычисления площади прямоугольного треугольника:
Площадь = (Основание * Высота) / 2
где:
- Основание - одна из сторон треугольника;
- Высота - прямая, проведенная из вершины прямого угла к основанию.
После подстановки значений основания и высоты в формулу, можно получить площадь прямоугольного треугольника.
Пример:
Пусть основание треугольника равно 5 см, а высота равна 3 см.
Площадь = (5 * 3) / 2 = 7.5 см²
Таким образом, площадь прямоугольного треугольника со стороной 5 см и высотой 3 см равна 7.5 квадратных сантиметров.
Пример вычисления площади прямоугольного треугольника
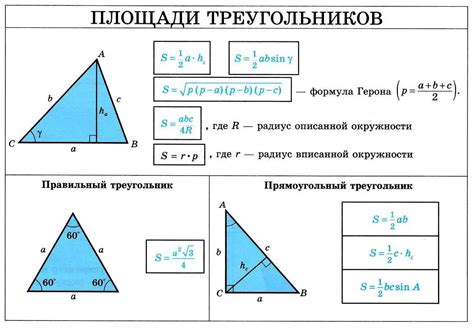
Для вычисления площади прямоугольного треугольника по высоте ${h}$ необходимо знать длину основания ${a}$ или ${b}$. Допустим, мы знаем длину основания ${a}$.
Формула для вычисления площади прямоугольного треугольника по высоте ${h}$ и основанию ${a}$:
| Формула | Пример |
|---|---|
| ${S = \frac{1}{2} \cdot a \cdot h}$ | ${S = \frac{1}{2} \cdot 4 \cdot 3 = 6}$ |
Где:
- ${S}$ - площадь прямоугольного треугольника;
- ${a}$ - длина основания прямоугольного треугольника;
- ${h}$ - высота прямоугольного треугольника.
Таким образом, если известны длина основания и высота прямоугольного треугольника, можно легко вычислить его площадь, умножив половину основания на высоту и поделив полученный результат на два.
Важные моменты при нахождении площади прямоугольного треугольника по высоте
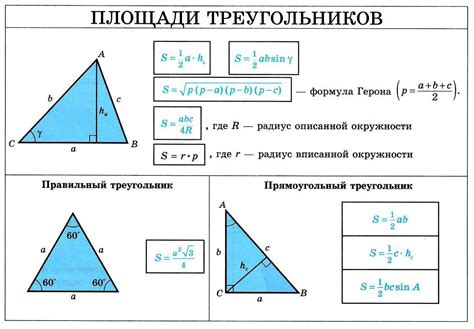
- Формула площади: Для определения площади прямоугольного треугольника по высоте необходимо знать формулу площади треугольника, которая равна половине произведения длины основания на высоту. То есть: S = (a * h) / 2, где S - площадь треугольника, a - длина основания и h - высота.
- Определение основания: Основание прямоугольного треугольника может быть любой из его сторон. Для нахождения площади по высоте необходимо знать длину именно этой стороны.
- Вычисление высоты: Для определения площади по высоте необходимо знать значение высоты, проходящей из вершины, лежащей напротив основания.
- Единицы измерения: При нахождении площади прямоугольного треугольника по высоте необходимо использовать одну и ту же единицу измерения для всех величин - основания, высоты и площади.
Учитывая эти важные моменты, вы сможете правильно находить площадь прямоугольного треугольника по его высоте. Эта операция часто применяется в геометрии и может быть полезной при решении различных задач и заданий.
Практическое применение нахождения площади прямоугольного треугольника по высоте
Навык вычисления площади прямоугольного треугольника по высоте может быть полезен в реальных ситуациях, где требуется измерить или оценить площадь подобных треугольников.
Например, одним из практических применений этого навыка является рассчет площади крыши. Крыша дома может иметь форму прямоугольного треугольника, особенно если скаты крыши имеют разный уклон. Зная высоту треугольника и длину одного из его катетов, можно легко вычислить площадь крыши и определить, сколько материала потребуется для ее покрытия.
Еще одним практическим применением является вычисление площади наклонного участка земли. Если участок имеет форму прямоугольника, но один из его углов находится не на одном уровне с другими, то можно использовать высоту прямоугольного треугольника, чтобы определить площадь этого участка земли.
Также, зная высоту прямоугольного треугольника, можно вычислить объем геометрических фигур, составленных из таких треугольников. Например, если нужно определить объем пирамиды, основание которой представляет собой систему прямоугольных треугольников, то зная площадь одного из таких треугольников и его высоту, можно легко вычислить объем всей пирамиды.
Таким образом, нахождение площади прямоугольного треугольника по высоте имеет множество практических применений в различных сферах, связанных с архитектурой, строительством и геометрией. Этот навык позволяет быстро и точно вычислять площади треугольников и использовать полученные значения в решении различных задач.
| Пример применения | Вычисление площади треугольника |
|---|---|
| Крыша дома | Измерьте высоту и длину одного из катетов и используйте формулу для нахождения площади. |
| Наклонный участок земли | Измерьте высоту и длину одного из катетов и используйте формулу для нахождения площади. |
| Вычисление объема пирамиды | Измерьте высоту и площадь одного из оснований и используйте формулу для нахождения объема. |