Равнобедренный треугольник – это треугольник, у которого две стороны равны. Особенностью равнобедренного треугольника является то, что высота, проведенная к основанию, делит его на два прямоугольных треугольника. Это свойство позволяет нам легко найти площадь такого треугольника при известных основании и боковой стороне.
Для вычисления площади равнобедренного треугольника мы можем использовать формулу: Площадь = (Основание * Высота) / 2. В данном случае высота треугольника будет равна половине длины боковой стороны, умноженной на корень квадратный из разности остатка от деления основания на 2 и половины длины боковой стороны. Это можно записать следующим образом: Высота = √(Боковая сторона^2 - (Основание/2)^2).
Используя эти формулы, мы можем легко найти площадь равнобедренного треугольника с известными основанием и боковой стороной. Просто подставьте значения в формулы и выполните вычисления.
Что такое равнобедренный треугольник?
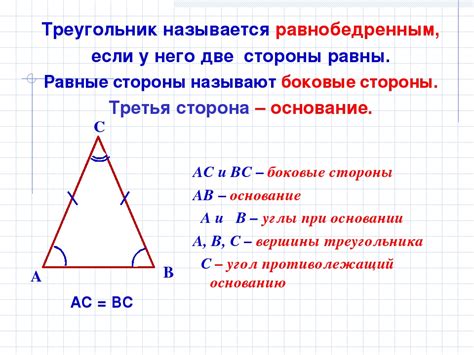
В равнобедренном треугольнике углы, противолежащие боковым сторонам, равны между собой. Величина каждого из этих углов называется углом при основании. Другой угол треугольника, противолежащий основанию, называется вершинным углом.
Для равнобедренного треугольника можно вычислить различные параметры, такие как площадь, периметр, радиус вписанной окружности и т.д. Площадь равнобедренного треугольника можно найти различными способами, включая использование основания и боковой стороны.
Определение и основные характеристики

В равнобедренном треугольнике основание считается боковой стороной, а две другие стороны называются равными. У такого треугольника существуют следующие характеристики:
- Основание: одна из сторон треугольника, которая отличается от остальных и является основой для вычисления площади.
- Боковая сторона: одна из равных сторон треугольника, которая также может использоваться при расчетах.
- Высота: перпендикуляр, опущенный из вершины треугольника на основание. Длина высоты также может использоваться при нахождении площади.
- Углы: в равнобедренном треугольнике два угла, прилежащих к основанию, равны между собой, а третий угол отличается.
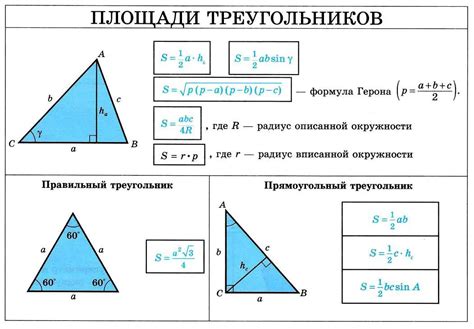
- Площадь: площадь равнобедренного треугольника можно найти, используя формулу: площадь = (основание * высота) / 2.
Знание этих основных характеристик поможет более точно и эффективно вычислить площадь равнобедренного треугольника, используя доступные данные.
Как найти высоту равнобедренного треугольника?
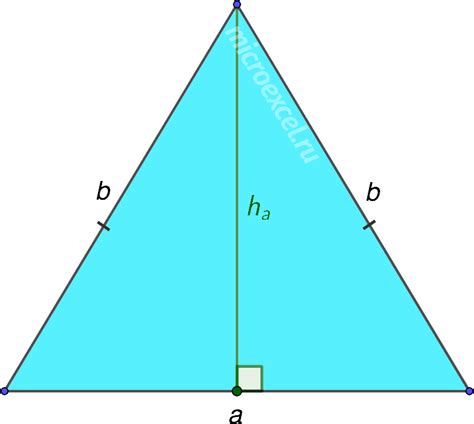
Чтобы найти высоту равнобедренного треугольника, можно использовать следующую формулу:
h = √(a^2 - (c/2)^2)
Где:
- h - высота равнобедренного треугольника
- a - длина основания треугольника
- c - длина боковой стороны треугольника (один из двух равных сторон)
Для использования этой формулы, необходимо знать длину основания и боковой стороны равнобедренного треугольника. Если эти данные известны, то вы можете просто подставить их в формулу и вычислить высоту треугольника.
Высота равнобедренного треугольника позволяет найти его площадь по формуле:
S = (a * h) / 2
Где:
- S - площадь равнобедренного треугольника
- a - длина основания треугольника
- h - высота равнобедренного треугольника
Используя эти формулы, вы сможете легко найти высоту и площадь равнобедренного треугольника, если у вас есть длина основания и боковой стороны.
Как найти площадь равнобедренного треугольника через высоту и основание?

Формула для вычисления площади равнобедренного треугольника через высоту и основание выглядит так:
S = (Основание * Высота) / 2
Где S - площадь треугольника, Основание - длина одного из оснований, Высота - высота, проведенная из вершины треугольника к основанию.
Чтобы применить эту формулу, нужно знать значения Основания и Высоты. Основание можно найти, зная длины боковых сторон треугольника или угол между ними. Высоту можно найти, зная длины основания и боковой стороны или угол между ними.
Теперь, когда ты знаешь, как найти площадь равнобедренного треугольника через высоту и основание, ты можешь легко решать задачи, связанные с этой геометрической фигурой.
Как найти площадь равнобедренного треугольника через боковую сторону и угол при основании?

Площадь треугольника = 0,5 * основание * высота.
В данном случае основание равно боковой стороне треугольника, а высоту можно найти, разделив длину боковой стороны на два и умножив на тангенс угла при основании:
Высота = (боковая сторона / 2) * tg(угол при основании).
Итак, формула площади равнобедренного треугольника через боковую сторону и угол при основании будет выглядеть:
Площадь треугольника = 0,5 * боковая сторона * ((боковая сторона / 2) * tg(угол при основании)).
Пример:
- Дано: боковая сторона = 6 см, угол при основании = 45 градусов.
- Площадь треугольника = 0,5 * 6 * ((6 / 2) * tg(45°)).
- Площадь треугольника = 0,5 * 6 * ((6 / 2) * 1).
- Площадь треугольника = 0,5 * 6 * (3 * 1).
- Площадь треугольника = 0,5 * 6 * 3.
- Площадь треугольника = 9 см².
Таким образом, площадь равнобедренного треугольника с боковой стороной 6 см и углом при основании 45 градусов равна 9 см².
Как найти площадь равнобедренного треугольника через радиус вписанной окружности?

Рассмотрим равнобедренный треугольник с основанием AB и радиусом вписанной окружности r. Мы можем найти площадь треугольника, используя формулу:
Площадь равнобедренного треугольника можно вычислить по следующей формуле:
S = (ab)/2
где a - длина основания треугольника AB, b - радиус вписанной окружности. Для вычисления площади треугольника, необходимо знать длину основания треугольника и радиус вписанной окружности.
Теперь, когда вы знаете, как можно найти площадь равнобедренного треугольника через радиус вписанной окружности, вы можете применять эту формулу для решения задач, связанных с данной фигурой.
Как найти площадь равнобедренного треугольника через радиус описанной окружности?

Площадь равнобедренного треугольника можно вычислить, используя радиус описанной окружности. Площадь треугольника можно найти по следующей формуле:
Площадь = (боковая сторона2 * π) / 4
Где боковая сторона - длина боковой стороны треугольника, π (пи) - математическая константа, приближенно равная 3.14159.
Чтобы определить радиус описанной окружности, можно использовать следующую формулу:
Радиус описанной окружности = (боковая сторона / 2) * √((4 * боковая сторона2) - (основание2))
Где основание - длина основания треугольника.
Зная радиус описанной окружности, можно подставить его значение в формулу для нахождения площади равнобедренного треугольника и получить итоговый результат.
Примеры расчетов площади равнобедренного треугольника
Для расчета площади равнобедренного треугольника с известными основанием и боковой стороной можно использовать следующую формулу:
- Найдите высоту треугольника, которая является перпендикулярной к основанию и проходит через его середину.
- Используя найденную высоту, умножьте ее на длину основания треугольника.
- Разделите полученное значение площади на 2, чтобы получить окончательный результат.
Например, если основание треугольника равно 8 см, а боковая сторона равна 10 см, то:
- Находим высоту треугольника: h = √(10^2 - (8/2)^2) = √(100 - 16) = √84 ≈ 9.17 см.
- Умножаем высоту на длину основания: S = 8 * 9.17 = 73.36 см^2.
- Разделяем полученное значение на 2: S = 73.36 / 2 = 36.68 см^2.
Таким образом, площадь данного равнобедренного треугольника будет приблизительно равна 36.68 см^2.
