Ромб - это четырехугольник, в котором все стороны имеют одинаковую длину. Он также обладает некоторыми интересными свойствами, которые помогут нам найти его площадь при известной стороне и диагонали. В этой статье мы рассмотрим подробные расчеты и объясним вам шаги, которые нужно предпринять, чтобы найти площадь ромба.
Важно отметить, что знание одной стороны и одной диагонали ромба недостаточно для точного расчета его площади. Но если у нас есть еще одна диагональ или другая известная сторона, мы можем использовать их, чтобы найти все необходимые данные.
Первым шагом в нахождении площади ромба является нахождение длины другой стороны. Упростим задачу, предположив, что нам известна одна сторона и одна диагональ. Длина второй стороны может быть найдена с помощью формулы Пифагора: вторая сторона = корень [(диагональ^2 - сторона^2) / 2]. Для более подробного объяснения этого расчета, давайте рассмотрим пример.
Методы расчета площади ромба с известной стороной и диагональю
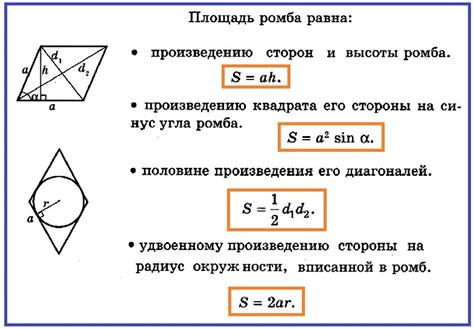
Если известна одна сторона ромба, то площадь можно найти по формуле: S = a*d, где a - известная сторона, d - диагональ.
Если известны две диагонали ромба, то площадь можно найти по формуле: S = (d1 * d2) / 2, где d1, d2 - диагонали.
Для расчета площади ромба с известной стороной можно измерить диагональ ромба перпендикулярно к известной стороне, а затем умножить эту диагональ на известную сторону. Если известны обе диагонали ромба, то их значения подставляются в формулу и вычисляется итоговая площадь.
Формула с использованием стороны и диагонали
Площадь ромба можно вычислить, зная длину одной стороны и одну из его диагоналей. Для этого нужно применить следующую формулу:
Площадь ромба = (диагональ * сторона) / 2
Для уточнения формулы следует понимать, что у ромба все стороны равны друг другу. Поэтому длина любой стороны ромба может служить в качестве известной переменной. Также следует учесть, что в ромбе диагонали взаимно перпендикулярны и делят друг друга пополам.
Следуя формуле, нужно умножить длину любой стороны ромба на длину известной диагонали и разделить полученное значение на 2. В результате получим площадь ромба.
Например, если известны сторона ромба равная 6 см и диагональ равная 8 см, то применяя формулу, получим:
- Площадь ромба = (8 * 6) / 2
- Площадь ромба = 48 / 2
- Площадь ромба = 24 см²
Таким образом, площадь ромба с данными параметрами составляет 24 квадратных сантиметра.
Формула через биссектрису и радиус вписанной окружности
Для расчета площади ромба по стороне и диагонали можно использовать формулу, основанную на биссектрисе и радиусе вписанной окружности.
Биссектриса ромба - это отрезок, который делит угол ромба пополам и проходит через центр ромба. Радиус вписанной окружности ромба - это расстояние от центра ромба до любой из его сторон.
Формула для расчета площади ромба через биссектрису и радиус вписанной окружности имеет следующий вид:
- Найдите биссектрису ромба, используя известную сторону и диагональ. Для этого можно воспользоваться теоремой синусов.
- Найдите радиус вписанной окружности ромба, используя формулу: радиус = половина биссектрисы.
- Рассчитайте площадь ромба по формуле: площадь = 2 * квадрат радиуса *(синус угла ромба).
Пользуясь этой формулой, вы можете легко и точно рассчитать площадь ромба с известной стороной и диагональю. Учитывайте, что значения сторон и диагоналей должны быть в одной единице измерения.