Знание геометрии играет важную роль в повседневной жизни. Одной из фигур, с которыми мы можем столкнуться, является трапеция. Трапеции можно встретить в архитектуре, инженерии, строительстве и даже в математических задачах.
Трапеция - это четырехугольник, у которого две противоположные стороны параллельны. Одна из особенностей трапеции заключается в том, что она может иметь разные углы и стороны. Если известны значения некоторых сторон и углов трапеции, то можно найти ее площадь.
Один из методов нахождения площади трапеции заключается в использовании угла между несколькими сторонами. Если угол измеряется в градусах и известны длины оснований трапеции, то площадь можно найти с помощью формулы, которая выглядит следующим образом:
S = ((a + b) / 2) * h
Где a и b - длины оснований, h - высота трапеции.
Теперь, когда у вас есть формула и некоторые советы, вы можете легко найти площадь трапеции по углу и сторонам. Используйте эту информацию, чтобы решать математические задачи или в реальной жизни, когда вам понадобится вычислить площадь трапеции.
Трапеция: что это?
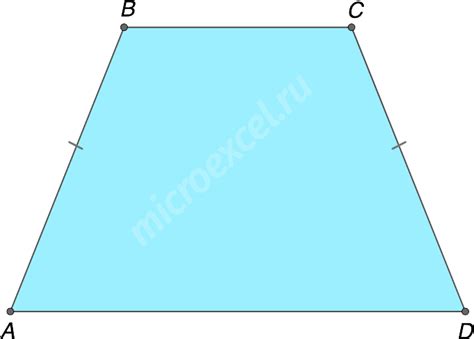
Трапеция может быть равнобедренной или неравнобедренной. В равнобедренной трапеции, пара оснований имеет одинаковые длины, а углы на основаниях равны. В неравнобедренной трапеции, все четыре стороны и углы могут иметь различные значения.
Трапеции могут использоваться во многих сферах, включая геометрию, строительство и инженерию. Они могут использоваться для расчета площадей и объемов различных форм, для создания стабильных и прочных конструкций, и для решения задач связанных с измерениями и углами.
Определение трапеции и ее частей

| Базы: | Длина основных параллельных сторон трапеции называется базами: |
| Вершины: | Точки пересечения боковых сторон трапеции называются вершинами: |
| Боковые стороны: | Строны трапеции, не являющиеся базами, называются боковыми сторонами: |
| Высота: | Расстояние между базами трапеции, перпендикулярное им, называется высотой: |
Знание этих частей трапеции важно для решения задачи на нахождение ее площади по углу и сторонам. Применяя соответствующую формулу, вы сможете вычислить площадь трапеции и использовать ее в различных контекстах, таких как строительство, геометрия или инженерное дело.
Угол трапеции и его значение для расчета площади
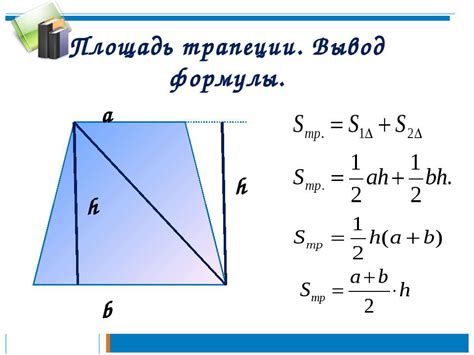
Рассмотрим два основных варианта угла трапеции:
1. Прямоугольная трапеция:
Если одним из углов трапеции является прямой угол (90 градусов), то такая трапеция называется прямоугольной. Для расчета площади такой трапеции можно воспользоваться следующей формулой:
Площадь = (сумма оснований) × (высота) / 2
Здесь основания - это две параллельные стороны трапеции, а высота - расстояние между основаниями, проведенное перпендикулярно к основанию.
2. Непрямоугольная трапеция:
Если все углы трапеции не являются прямыми, то такая трапеция называется непрямоугольной. Для расчета площади такой трапеции используется другая формула, которая зависит от значений сторон и углов:
Площадь = ((a + b) × h) / 2
Здесь a и b - длины оснований, а h - высота, которая определяется как расстояние между основаниями, проведенное перпендикулярно к одному из оснований, умноженное на синус угла, противолежащего основанию b.
Зная значение угла и длины сторон, можно правильно выбрать формулу и рассчитать площадь трапеции, что может быть полезно при выполнении различных задач и расчетов.
Как найти площадь трапеции по углу и сторонам
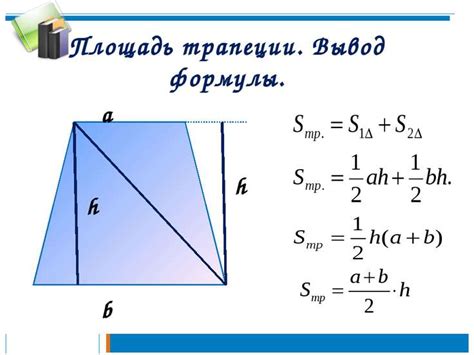
Формула для нахождения площади трапеции по углу и сторонам выглядит следующим образом:
| Сторона трапеции | Значение |
|---|---|
| AB | a |
| BC | b |
| CD | c |
| DA | d |
Угол при основании AB обозначим как α. Тогда площадь трапеции S может быть вычислена по формуле:
S = 0.5 * (a + c) * h
где h - высота трапеции, которая может быть вычислена по формуле:
h = (b - d) * tan(α)
Теперь, зная значения сторон трапеции и угол при основании AB, мы можем использовать эти формулы для вычисления площади.
Формула для нахождения площади трапеции по углу и основаниям
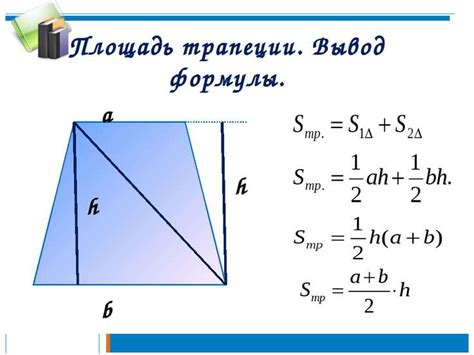
Площадь трапеции можно найти, зная угол между основаниями и значения этих оснований. Для этого существует специальная формула, которая выглядит следующим образом:
S = (a + b) * h / 2
Где:
- S - площадь трапеции
- a, b - длины оснований трапеции
- h - высота трапеции, которая перпендикулярна основаниям и измеряется по углу между ними
Для расчёта площади трапеции по этой формуле необходимо знать значения оснований и угол между ними. Используя эту формулу, вы можете легко и быстро вычислить площадь трапеции по данным параметрам.
Практический пример и решение

Допустим, у нас есть трапеция с углом 60 градусов, основаниями 5 и 8 см, и боковыми сторонами 6 и 6 см. Нам нужно найти площадь этой трапеции.
1. Сначала мы должны найти высоту трапеции. Для этого мы можем использовать теорему Пифагора, так как у нас есть боковые стороны и угол.
2. Используя теорему Пифагора, мы можем найти высоту: h = √(6² - 3²) = √27 ≈ 5.2 см.
3. Затем мы можем использовать формулу для площади трапеции: S = (a + b) * h / 2, где a и b - основания трапеции, h - высота.
4. Подставим значения: S = (5 + 8) * 5.2 / 2 = 54.4 см².
Таким образом, площадь этой трапеции составляет примерно 54.4 см².