Треугольник - одна из самых простых и распространенных геометрических фигур, которая обладает множеством интересных свойств и особенностей. Большинство задач, связанных с треугольниками, требуют нахождения их площади. В данной статье мы рассмотрим один из способов нахождения площади треугольника, основанный на радиусе описанной окружности.
Радиус описанной окружности - это отрезок, проведенный из центра окружности до любой точки на ее границе. Описанная окружность может быть построена вокруг треугольника, когда ее центр совпадает с центром описанной окружности треугольника.
Площадь треугольника можно найти по разным формулам, в зависимости от известных параметров. Однако, если нам известен радиус описанной окружности треугольника, мы можем использовать следующую формулу для расчета его площади:
S = (r2 * sin(A) * sin(B) * sin(C)) / (4 * sin((A + B + C) / 2)),
где r - радиус описанной окружности, A, B, C - углы треугольника, S - площадь треугольника.
Теперь мы знаем, как найти площадь треугольника по радиусу описанной окружности и можем приступать к решению задач, которые связаны с данным фактом.
Как найти площадь треугольника
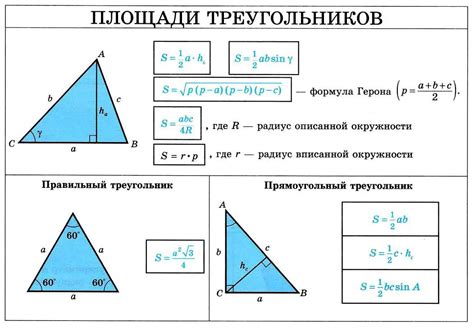
Площадь треугольника можно найти различными способами, в зависимости от доступной информации о треугольнике. Рассмотрим несколько методов:
- Метод по формуле Герона:
- Найдите полупериметр треугольника, сложив длины всех его сторон и разделив полученную сумму на два.
- Используя формулу Герона S = √(p(p-a)(p-b)(p-c)), где S - площадь треугольника, а, b и c - длины его сторон, найдите площадь треугольника.
- Найдите основание (одну сторону) треугольника и его высоту, перпендикулярную к этой стороне.
- Умножьте длину основания на длину высоты и разделите полученное произведение на 2, чтобы найти площадь треугольника.
- Найдите длины сторон треугольника, зная радиус описанной окружности и применив формулу a = 2Rsin(A), где R - радиус описанной окружности, а A - мера угла, противоположного стороне a.
- Используя полученные значения сторон треугольника, примените метод по формуле Герона для нахождения площади треугольника.
Используя один из этих методов, вы сможете легко найти площадь треугольника в различных ситуациях.
Метод по радиусу описанной окружности

Площадь треугольника можно вычислить, зная радиус его описанной окружности. Для этого используется следующая формула:
S = (r2 * sin(A) * sin(B) * sin(C)) / (4 * sin(A+B) * sin(B+C) * sin(C+A))
где:
- S - площадь треугольника
- r - радиус описанной окружности
- A, B, C - углы треугольника
Для использования данной формулы необходимо знать радиус описанной окружности треугольника.
Метод по радиусу описанной окружности можно применять при необходимости найти площадь треугольника, если известен радиус его описанной окружности и значения углов треугольника.
Используя данный метод, вы можете упростить вычисление площади треугольника и получить точный результат.