Интеграл является одним из основных понятий математического анализа. Он позволяет решать различные задачи, связанные с вычислением площадей, объемов или распределения вероятностей. Однако при работе с интегралами иногда возникает необходимость найти их производную.
На первый взгляд это может показаться сложной задачей, но на самом деле есть несколько методов, которые позволяют легко найти производную интеграла. В этой статье мы рассмотрим основные из них и приведем примеры с подробными пошаговыми объяснениями.
Существует несколько способов нахождения производной интеграла, таких как формула Лейбница, формула Ньютона-Лейбница и интегрирование по частям. Каждый из них имеет свои преимущества и ограничения, поэтому важно знать, когда и как применять каждый из них.
Определение производной и интеграла

Производная функции
Производная функции определяется как предел отношения приращения функции к соответствующему приращению аргумента, при стремлении приращения аргумента к нулю:
$$f'(x) = \lim_{{\Delta x \to 0}}\frac{{\Delta f}}{{\Delta x}} = \lim_{{\Delta x \to 0}}\frac{{f(x + \Delta x) - f(x)}}{{\Delta x}}$$
Производная функции характеризует мгновенную скорость изменения значения функции в каждой точке. Она также может быть интерпретирована как угол наклона касательной линии к графику функции в данной точке.
Интеграл функции
Интеграл функции определяется как площадь под ее графиком на заданном интервале. Интеграл функции обозначается символом $$\int$$ и записывается следующим образом:
$$\int_{{a}}^{{b}} f(x) dx$$
Геометрический смысл интеграла - это площадь прямоугольника, ограниченного графиком функции, осью абсцисс и вертикальными прямыми $$x = a$$ и $$x = b$$. Интеграл функции также может быть интерпретирован как накопленная сумма площадей бесконечно малых прямоугольников, каждая из которых имеет ширину $$dx$$ и высоту $$f(x)$$.
Существует два типа интегралов: определенный и неопределенный. Определенный интеграл вычисляет конкретное значение площади под графиком функции на определенном интервале, а неопределенный интеграл находит функцию, производная которой является исходной функцией.
Определение производной и интеграла является основой дифференциального и интегрального исчисления, и их изучение открывает широкий спектр математических методов и понятий для анализа и решения различных задач.
Зачем находить производную интеграла?

Производная интеграла представляет собой новую функцию, которая описывает скорость изменения значения интеграла. Эта функция может быть полезна для различных приложений, таких как оптимизация, физические моделирования и анализ экономических данных.
Также, нахождение производной интеграла позволяет решать задачи определения площадей под кривыми, определения среднего значения функции и нахождения общего решения некоторых дифференциальных уравнений.
Знание производной интеграла является основой для более сложных методов исследования функций, таких как интегральное исчисление, дифференциальные уравнения и теория вероятности.
Итак, нахождение производной интеграла является неотъемлемой частью изучения математики и имеет широкое практическое применение в науке, технике и других областях. Понимание этого понятия позволяет углубить знания о функциях и их свойствах, а также решать разнообразные задачи в практическом применении.
Основные методы нахождения производной интеграла

Существуют несколько методов нахождения производной интеграла:
- Прямое дифференцирование интеграла.
- Использование формулы Лейбница для дифференцируемой функции.
- Применение формулы Ньютона-Лейбница.
1. Прямое дифференцирование интеграла:
Для нахождения производной интеграла постоянно функции можно воспользоваться прямым дифференцированием. Для этого достаточно заменить пределы интегрирования на переменные и применить правило дифференцирования для функции.
2. Использование формулы Лейбница для дифференцируемой функции:
Формула Лейбница позволяет дифференцировать интеграл с переменным верхним пределом, где подынтегральная функция является дифференцируемой. Для этого необходимо продифференцировать исходную функцию и подставить верхний предел вместо переменной.
3. Применение формулы Ньютона-Лейбница:
Формула Ньютона-Лейбница устанавливает связь между интегралом и первообразной функции. Для нахождения производной интеграла с переменными пределами необходимо продифференцировать первообразную и подставить пределы интегрирования.
Применение указанных методов позволяет эффективно находить производную интеграла и использовать ее результаты в различных областях математики, физики и других наук.
Примеры нахождения производной интеграла

Ниже приведены несколько примеров, которые помогут вам лучше понять, как найти производную интеграла.
Пример 1:
Пусть f(x) – непрерывная функция, заданная на отрезке [a, b]. Известно, что
F(t) = ∫[a, t] f(x) dx
Составим функцию g(t) = ∫[a, b] f(x) dx, тогда производная этой функции будет равна
g'(t) = d/dt[∫[a, b] f(x) dx] = f(t)
Пример 2:
Пусть f(x) и g(x) – непрерывные функции, заданные на отрезке [a, b]. Известно, что
F(t) = ∫[a, t] f(x) dx
G(t) = ∫[a, t] g(x) dx
Тогда производная функции h(t) = F(t) * G(t) будет равна
h'(t) = d/dt[F(t) * G(t)] = f(t) * G(t) + F(t) * g(t)
Пример 3:
Пусть f(x) – непрерывная функция, заданная на интервале (a, b]. Тогда производная функции g(x) = ∫[a, x] f(t) dt будет равна
g'(x) = d/dx[∫[a, x] f(t) dt] = f(x)
Пример 4:
Пусть f(x) – непрерывная функция, заданная на интервале [a, b). Тогда производная функции g(x) = ∫[x, b) f(t) dt будет равна
g'(x) = d/dx[∫[x, b) f(t) dt] = -f(x)
Надеюсь, эти примеры помогут вам находить производные интегралов и лучше понять их свойства.
Формулы для вычисления производной интеграла
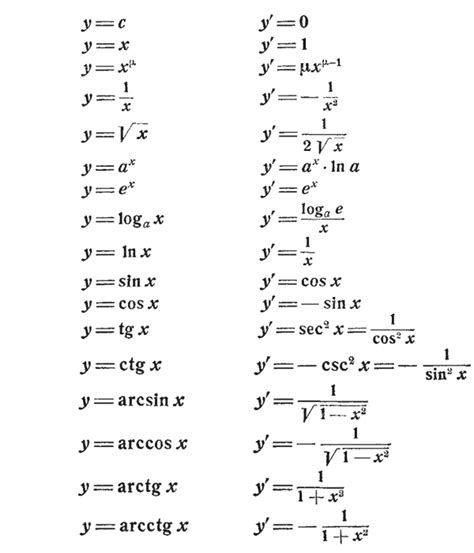
Вычисление производной интеграла требует применения специальных формул, которые позволяют найти производную от функции и затем взять интеграл от полученного выражения. В данном разделе рассмотрим основные формулы для вычисления производной интеграла.
- Формула Ньютона-Лейбница: Если функция \(F(x)\) является первообразной непрерывной функции \(f(x)\) на отрезке \([a, b]\), то интеграл этой функции на отрезке \([a, b]\) можно выразить как разность значений ее первообразной в точках \(a\) и \(b\):
- Формула дифференцирования интеграла: Если функция \(f(x, t)\) непрерывна на прямоугольнике \([a, b] \times [c, d]\) и \(F(t)\) является первообразной функции \(f(x, t)\), то функция \(F(x)\), заданная интегралом \(\int_c^d f(x, t) dt\) является первообразной функции \(f(x, t)\) по переменной \(x\) на отрезке \([a, b]\), и ее производная по переменной \(x\) равна интегралу от производной функции \(f(x, t)\) по переменной \(x\):
- Формула Лейбница: Если функция \(f(x, t)\) непрерывна на прямоугольнике \([a, b] \times [c, d]\) и удовлетворяет некоторым условиям регулярности, то интеграл с переменным верхним пределом от этой функции является дифференцируемой по переменной \(x\) функцией, и его производная по переменной \(x\) можно выразить с помощью интеграла от частной производной функции \(f(x, t)\):
\[ \int_a^b f(x) dx = F(b) - F(a) \]
\[ \frac{d}{dx} \int_c^d f(x, t) dt = \int_c^d \frac{\partial f}{\partial x}(x, t) dt \]
\[ \frac{d}{dx} \int_a^x f(x, t) dt = f(x, x) + \int_a^x \frac{\partial f}{\partial x}(x, t) dt \]
Эти формулы позволяют находить производные интегралов, что может быть полезно при решении различных математических и физических задач. Они могут быть применены для вычисления производных интегралов как вручную, так и при использовании компьютерных программ и систем символьных вычислений.
Практическое применение производной интеграла

Производная интеграла имеет широкое практическое применение в различных областях, включая физику, экономику, статистику и инженерию. Ниже приведены некоторые конкретные примеры использования производной интеграла:
- Определение скорости: Производная интеграла функции, представляющей путь, позволяет вычислить скорость движения. Например, если у нас есть функция, описывающая положение транспортного средства в зависимости от времени, то производная интеграла этой функции даст нам скорость изменения положения.
- Вычисление площади и объема: Производная интеграла может быть использована для вычисления площади под кривой или объема тела. Например, если у нас есть функция, описывающая плотность материала в зависимости от расстояния, то интеграл этой функции может дать нам массу материала в определенном интервале, а производная интеграла этой функции позволит нам рассчитать изменение массы.
- Анализ экономических данных: Производная интеграла может быть использована для анализа экономических данных, таких как спрос, предложение, цены и т.д. Например, производная интеграла функции, описывающей спрос на товар, может помочь определить момент, когда спрос будет наибольшим.
- Инженерные приложения: Производная интеграла помогает инженерам рассчитать различные параметры системы, такие как сила, давление, тепловой поток и т.д. Например, производная интеграла функции, описывающей силу, действующую на объект, может помочь в определении момента, когда сила будет наибольшей.
В целом, производная интеграла является мощным инструментом для анализа и решения различных задач, которые возникают на практике. Этот метод позволяет нам получить информацию о скорости изменения, площади, объеме, спросе, предложении, силе и многом другом. Знание и понимание этого инструмента помогает нам более эффективно моделировать и анализировать реальные процессы и явления.