Конус – это геометрическое тело, которое имеет форму усеченного конуса, но не имеет круговой основы. Одним из важных параметров конуса является его образующая, которая является линией, соединяющей вершину конуса и любую точку на его образующей окружности (боковой поверхности).
Если вам известен объем конуса и вы хотите найти его радиус образующей, вам потребуется использовать формулу для объема конуса:
V = (1/3) * π * r2 * h
где V - объем конуса,π - число Пи (примерно равно 3,14), r - радиус образующей, h - высота конуса.
Для нахождения радиуса образующей нам потребуется провести небольшие преобразования и перейти от формулы для объема к формуле, содержащей радиус образующей:
r = ∛((3 * V) / (π * h))
Теперь, зная объем конуса и высоту, вы можете легко найти радиус его образующей.
Что такое объем конуса и как его найти?

Формула для вычисления объема конуса зависит от известных параметров. Если известны радиус основания конуса (R) и высота конуса (h), то объем вычисляется по формуле:
Объем = (π * R² * h) / 3,
где π – математическая константа, примерное значение которой равно 3,14159. Если радиус основания и высота конуса измеряются в одних и тех же единицах длины, то результат будет выражен в кубических единицах этой длины.
Для вычисления объема конуса при известном радиусе основания и высоте, нужно возвести радиус в квадрат, умножить на высоту, умножить на число π, а затем разделить полученное значение на 3.
Если известен только объем конуса и радиус основания, то высоту можно найти с помощью обратной формулы:
Высота = (3 * V) / (π * R²),
где V – объем конуса.
Изучение формулы для вычисления объема конуса позволяет решать задачи на его объем и находить неизвестные параметры конуса.
Теория конусов
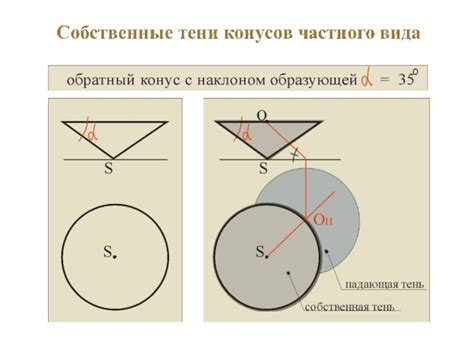
У конуса есть несколько ключевых параметров, которые играют важную роль в его описании:
1. Радиус основания (R) - это расстояние от центра основания конуса до любой точки его окружности.
2. Высота (H) - это расстояние от вершины конуса до основания, проходящее перпендикулярно основанию.
3. Радиус образующей (l) - это расстояние от вершины конуса до любой точки на его боковой поверхности. Образующая является гипотенузой прямоугольного треугольника, образованного высотой и радиусом основания.
Радиус образующей может быть вычислен с использованием формулы:
l = √(R^2 + H^2)
Где l - радиус образующей, R - радиус основания, H - высота конуса.
Из этой формулы можно выразить радиус образующей, если известны радиус основания и высота конуса.
Формула объема конуса
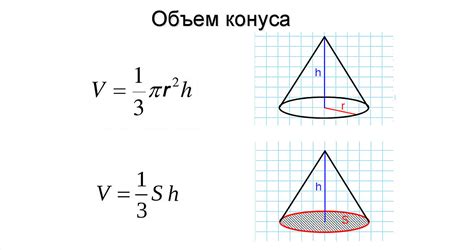
Объем V конуса можно вычислить по формуле:
V = (1/3) * π * r2 * h,
где:
- V - объем конуса,
- π - математическая константа, приближенно равняющаяся 3.14159,
- r - радиус образующей конуса,
- h - высота конуса.
Данная формула позволяет найти объем конуса, если известны его радиус и высота. Радиус образующей является одним из ключевых параметров, влияющих на объем конуса. Чтобы найти радиус образующей по известному объему конуса, формула объема конуса может быть модифицирована следующим образом:
r = √((3V)/(πh)),
где:
- r - радиус образующей конуса,
- V - объем конуса,
- π - математическая константа, приближенно равняющаяся 3.14159,
- h - высота конуса.
Таким образом, зная объем и высоту конуса, можно найти радиус его образующей с помощью данной формулы.
Известный объем - неизвестный радиус

Когда мы знаем объем конуса, но не знаем радиус его образующей, нам необходимо использовать формулу для нахождения радиуса.
Формула для нахождения радиуса конуса при известном объеме выглядит следующим образом:
1. Найдите значение радиуса величиной V3, где V - общий объем конуса, а 3 - число, которое соответствует неизвестному радиусу.
2. Используйте формулу для нахождения радиуса, где r - радиус, а V - объем конуса: r = ∛(3V/π).
3. Подставьте вместо V известное значение объема и вычислите радиус конуса по формуле.
4. Полученное значение радиуса является ответом на поставленную задачу. Убедитесь, что ответ корректен и имеет правильные единицы измерения.
Найденный радиус конуса при известном объеме поможет уточнить параметры фигуры и использовать их в дальнейших расчетах или построениях.
Шаги по нахождению радиуса конуса
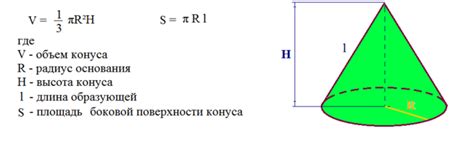
Шаг 1: Определите объем конуса, известный вам.
Шаг 2: Используя формулу для объема конуса, подставьте известные значения: V = (1/3) * π * r^2 * h, где V - объем конуса, π - число пи (3,14), r - радиус основания конуса, h - высота конуса.
Шаг 3: Разрешите уравнение для радиуса r и решите его.
Шаг 4: Подставьте найденное значение радиуса в формулу для объема конуса, чтобы проверить правильность решения.
Шаг 5: Проверьте единицы измерения, чтобы удостовериться, что они согласуются с заданными значениями.
Пример расчета
Рассмотрим конкретный пример, чтобы понять, как найти радиус образующей конуса при известном объеме.
Пусть нам известен объем конуса, равный 1000 см³, и мы хотим найти радиус его образующей. Для начала вспомним формулу для объема конуса:
Объем конуса = 1/3 * П * r² * h,
где r - радиус образующей, h - высота конуса.
Зная объем конуса, мы можем переписать формулу, чтобы найти радиус:
r² * h = 3 * V / П,
где V - объем конуса.
В нашем примере, V = 1000 см³, поэтому:
r² * h = 3 * 1000 / П,
или
r² * h = 955.031,
где П примерно равно 3.14159.
Теперь мы можем приступить к поиску значения радиуса. Допустим, мы выбрали произвольную высоту конуса, равную 10 см. Подставим значения в формулу:
| r² * h = | 955.031 |
| r² * 10 = | 955.031 |
| r² = | 955.031 / 10 |
| r² = | 95.5031 |
| r ≈ | √95.5031 |
| r ≈ | 9.7712 |
Таким образом, при высоте конуса, равной 10 см, радиус его образующей составляет примерно 9.7712 см.
Как использовать радиус образующей конуса?

Вот некоторые способы использования радиуса образующей конуса:
- Расчет общей поверхности: При известном радиусе образующей и высоте конуса можно легко вычислить его общую поверхность. Формула для этого расчета следующая: S = π*r*(r + l), где S - общая поверхность, r - радиус основания, l - длина образующей. Зная значение радиуса образующей, можно точно определить размер общей поверхности конуса.
- Вычисление объема: Используя радиус образующей и высоту конуса, можно определить его объем. Формула для вычисления объема конуса выглядит следующим образом: V = (1/3) * π * r^2 * h, где V - объем конуса, r - радиус основания, h - высота конуса. Зная радиус образующей, можно легко найти объем этой геометрической фигуры.
- Расчет площади основания: Используя радиус образующей и высоту конуса, можно найти площадь основания конуса. Формула для этого расчета следующая: A = π * r^2, где A - площадь основания, r - радиус основания. Эта характеристика конуса также может быть полезной при решении задач.
- Определение угла наклона: Зная значение радиуса образующей и высоты конуса, можно рассчитать угол наклона боковой поверхности конуса. Формула для этого расчета следующая: α = arctan(r/h), где α - угол наклона боковой поверхности, r - радиус основания, h - высота конуса. Этот угол может быть полезен при различных инженерных расчетах.
Таким образом, радиус образующей конуса является важной характеристикой, которую можно использовать для решения различных задач и расчетов, связанных с конусом.
Ошибки при нахождении радиуса конуса
При расчете радиуса конуса по известному объему возможны ошибки, которые могут повлиять на точность результатов. Некоторые из наиболее распространенных ошибок включают:
1. Неправильное использование формулы
Для нахождения радиуса конуса по известному объему необходимо использовать правильную формулу. Ошибка в использовании формулы может привести к некорректным результатам. Убедитесь, что вы правильно подобрали формулу для конуса.
2. Неправильно указаны единицы измерения
При расчете радиуса конуса необходимо быть внимательным к единицам измерения. Неправильно указанные единицы измерения могут привести к некорректным значениям радиуса. Внимательно проверьте, что вы используете правильные единицы измерения во всех расчетах.
3. Неправильное округление
При расчетах необходимо быть осторожным с округлением. Неправильное округление может привести к погрешности в результатах. Убедитесь, что вы округляете значения до нужного количества знаков после запятой.
4. Неучтенные факторы
При нахождении радиуса конуса по известному объему необходимо учесть все факторы, которые могут влиять на результаты расчетов, например, температуру или другие параметры окружающей среды. Неучтенные факторы могут привести к неточным значениям радиуса.
Избегая указанных ошибок при нахождении радиуса конуса, можно достичь более точных результатов и провести расчеты без упущений.