Правильный треугольник - это треугольник, у которого все стороны равны, а все углы - 60 градусов. Такой треугольник один из самых простых геометрических фигур. Вместе с тем, в правильном треугольнике есть много интересных свойств, которые могут быть полезными при решении задач.
Одна из таких задач - найти радиус вписанной окружности по стороне. Для этого, в первую очередь, необходимо знать, что вписанная окружность правильного треугольника проходит через середины его сторон. То есть, если мы проведем прямые, соединяющие середины сторон, эти прямые будут касаться окружности.
Далее, необходимо помнить, что радиус вписанной окружности является расстоянием от центра окружности до любой стороны треугольника. Для правильного треугольника это расстояние можно найти по формуле: радиус = сторона / (2 * тангенс угла).
Вычисление радиуса вписанной окружности правильного треугольника
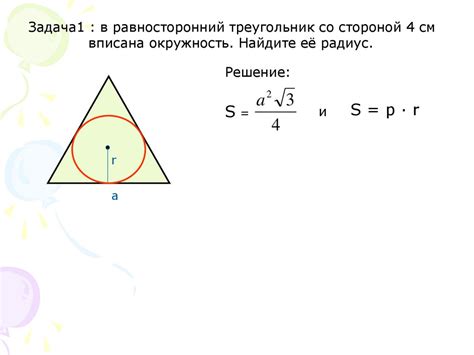
Радиус вписанной окружности правильного треугольника может быть вычислен с использованием формулы, которая основывается на свойствах этого треугольника.
Для начала, воспользуемся тем фактом, что вписанная окружность правильного треугольника делит все стороны треугольника на равные части. Таким образом, каждая сторона треугольника равна двум радиусам вписанной окружности.
Также мы знаем, что каждый угол равностороннего треугольника равен 60 градусам. Это позволяет нам применить тригонометрические формулы для нахождения радиуса окружности.
Используя формулу, вы можете выразить радиус вписанной окружности, как:
Где r - радиус окружности, a - сторона треугольника, π - число пи, tan - тангенс.
Таким образом, зная сторону равностороннего треугольника, мы можем использовать эту формулу для вычисления радиуса вписанной окружности.
Как найти радиус вписанной окружности
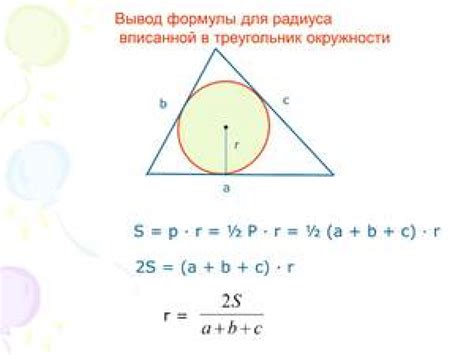
Вписанная окружность находится внутри многоугольника таким образом, что каждая сторона многоугольника касается окружности только в одной точке. Для правильного треугольника радиус вписанной окружности может быть найден следующим образом.
- Найдите длину одной из сторон правильного треугольника. Это может быть сделано с помощью формулы, зная радиус описанной окружности и применяя соответствующие геометрические связи.
- Поделите длину стороны на √3. Это будет равно радиусу вписанной окружности.
Теперь вы знаете, как найти радиус вписанной окружности правильного треугольника по стороне. Этот метод также может быть применен для нахождения радиуса вписанной окружности других правильных многоугольников.