Синус - это одна из тригонометрических функций, которая является отношением противолежащего катета к гипотенузе прямоугольного треугольника. Обычно синус находят для угла в радианах, но также можно вычислить его значение для целого числа. Это может быть полезно во многих областях, таких как математика, физика, компьютерная графика и другие.
Для нахождения синуса целого числа можно использовать таблицу значений синуса или математические формулы. Если нужно найти приближенное значение синуса целого числа, можно воспользоваться рядом Тейлора, который представляет синус в виде бесконечной суммы полиномов. Однако, для больших чисел это может быть долгим и ресурсоемким процессом.
Более эффективным способом является использование библиотеки или функции, предоставляемой в выбранном программном языке. Например, в языке Python для вычисления синуса можно использовать функцию sin() из модуля math. Для языка JavaScript доступна функция Math.sin(). Если вы пишете программу на другом языке, то лучше обратиться к официальной документации или сообществу разработчиков для получения информации о доступных методах и функциях для вычисления синуса.
Важно помнить, что значения синуса могут быть в диапазоне от -1 до 1, и они могут быть положительными или отрицательными в зависимости от угла. Зная эти особенности, можно с уверенностью использовать вычисленные значения синуса целого числа в своих математических вычислениях.
Что такое синус целого числа?
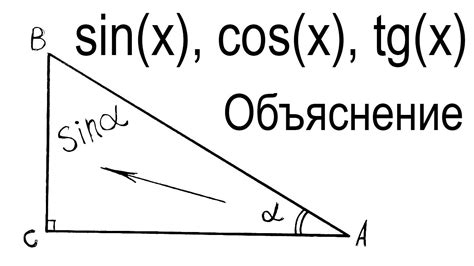
Однако, чтобы рассчитать синус целого числа, следует учесть, что результат функции синуса является вещественным числом, а значение синуса целого числа может быть представлено в виде периодической функции с периодом 2π. Для целых чисел синус может принимать значения от -1 до 1.
Синус целого числа имеет некоторые интересные свойства и применения в различных областях, таких как физика, математика и информатика. Например, синус используется для описания гармонических колебаний, а также в построении графиков функций и решении уравнений.
Расчет синуса целого числа можно выполнить с использованием математических формул или с помощью специализированных программных инструментов, таких как калькуляторы и программы для научных расчетов.
| Целое число | Синус |
|---|---|
| 0 | 0 |
| 1 | 0.8414709848 |
| 2 | 0.9092974268 |
| 3 | 0.1411200081 |
| 4 | -0.7568024953 |
| 5 | -0.9589242747 |
Определение и основные свойства

Синус числа может быть выражен как бесконечная десятичная дробь, представляющая значение от -1 до 1. В математике, синус обычно обозначается символом "sin".
Основные свойства синуса:
- Синус целого числа находится с помощью тригонометрических таблиц или с помощью математических функций в языках программирования.
- Синус четного числа всегда равен нулю, так как в прямоугольном треугольнике сторона противоположного катета равна нулю.
- Синус нечетного числа всегда лежит в интервале (-1, 1), так как противоположная сторона всегда меньше гипотенузы.
- Синус симметричен относительно начала координат, то есть sin(-x) = -sin(x).
- Синус имеет период 2π, что означает, что sin(x) = sin(x + 2π) для любого действительного числа x.
Использование синуса часто встречается в науке, инженерии и углубленных математических расчетах для решения различных задач, связанных с колебаниями, периодичностью и гармоническими функциями.
Формула для вычисления синуса целого числа
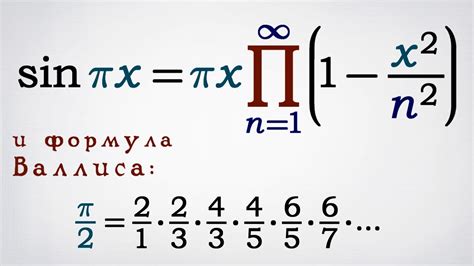
Синус целого числа можно вычислить с помощью формулы, используя тригонометрические функции. Формула основана на применении тригонометрических соотношений и свойств синуса.
Для вычисления синуса целого числа x можно использовать следующую формулу:
sin(x) = sin(x - 2πk)
где k - любое целое число, такое что sin(x) не выходит за пределы от -1 до 1.
Это свойство синуса позволяет сократить вычисления из-за периодической природы синуса. Если x - целое число, то значение sin(x) равно значению sin(x - 2π) или sin(x + 2π) и так далее.
Таким образом, для вычисления синуса целого числа достаточно найти значение синуса в пределах периода исходного числа.
Примечание: для удобства вычислений существует множество табличных значений синуса для целых чисел. Использование таких таблиц может значительно ускорить процесс вычисления синуса целого числа.
Таблица значений синуса для целых чисел
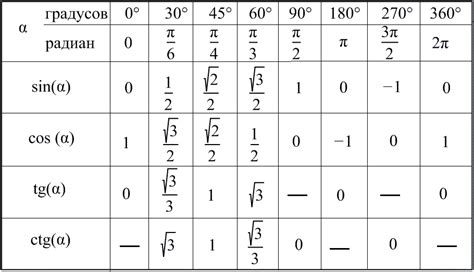
Угол (в градусах)
Синус
0
0
30
0.5
45
0.70710678118
60
0.86602540378
90
1
120
0.86602540378
135
0.70710678118
150
0.5
180
0
210
-0.5
225
-0.70710678118
240
-0.86602540378
270
-1
300
-0.86602540378
315
-0.70710678118
330
-0.5
360
0
График синусоиды для целых значений
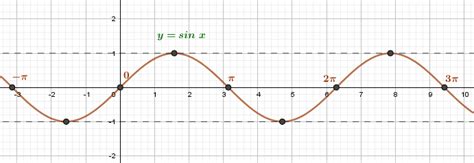
Для целых значений аргумента синусоиды, таких как -1, 0, 1, 2 и т. д., график имеет простую структуру. Значение синуса для целого аргумента можно найти, используя таблицы значений синуса или математические формулы.
На графике синусоиды для целых значений видна периодичность функции. График повторяется через равные промежутки, образуя волну с постоянной амплитудой и частотой. Амплитуда - это максимальное значение графика синусоиды, а частота - количество повторений волны в единицу времени или расстояния.
График синусоиды для целых значений может быть полезен при решении задач в различных областях, таких как физика, математика, инженерия и др. Часто такой график используется для моделирования колебаний, волновых процессов и гармонических функций.
Практическое применение синуса целых чисел

Вот несколько практических применений синуса целых чисел:
- Измерение высоты: Синус может использоваться для измерения высоты различных объектов. Например, если у вас есть треугольник, вы можете использовать синус, чтобы найти высоту этого треугольника.
- Прогноз погоды: Синус может быть использован для прогнозирования изменений атмосферного давления. Путем анализа изменений синуса, вы можете предсказать, будет ли погода ухудшаться или улучшаться.
- Звуковые волны: Синус также широко используется в области акустики и аудио-техники. Он помогает анализировать и воспроизводить звуковые волны.
- Электроника: Синус может быть использован для анализа и генерации электрических сигналов. Он часто используется в области радиоинженерии и связи.
Это лишь некоторые из возможных применений синуса целых чисел. Он находит свое применение во многих других областях, включая физику, медицину, экономику и многое другое.
Важно помнить, что синус является функцией, которая работает как с действительными числами, так и с комплексными числами, и ее применение может быть очень разнообразным в зависимости от контекста и задачи.
В этой статье мы рассмотрели несколько способов нахождения синуса целого числа. Мы начали с использования библиотечной функции в языках программирования, которая возвращает значение синуса. Затем мы рассмотрели метод, основанный на использовании разложения в ряд Тейлора синуса, который позволяет приближенно вычислить значение синуса числа.
Также мы изучили аппроксимацию синуса при помощи геометрической фигуры – окружности, а также метод преобразования синуса косинуса и обратно при помощи тригонометрических тождеств.
В завершении статьи мы рассмотрели вариант программной реализации нахождения синуса целого числа и обратили внимание на особенности работы с памятью и числами с плавающей запятой.
Выбор конкретного метода нахождения синуса целого числа зависит от требований проекта, доступных ресурсов и ожидаемой точности результата. Однако, независимо от выбранного метода, необходимо учитывать ограничения и особенности выбранного языка программирования и аппаратной архитектуры. Это позволит получить наиболее точный и эффективный результат в каждом конкретном случае.