Синус и косинус - это две основные тригонометрические функции, которые широко используются в математике и науке. Синус обозначается как sin, а косинус - как cos. Обратные функции называются арксинусом и арккосинусом соответственно.
Синус и косинус появляются при рассмотрении треугольников на плоскости. Синус определяется отношением длины противоположной стороны к гипотенузе, а косинус - отношением длины прилегающей стороны к гипотенузе.
Если известно значение косинуса угла, мы можем использовать формулу для нахождения значения синуса. Формула для нахождения синуса по косинусу выглядит следующим образом:
sin(x) = √(1 - cos^2(x))
Где x - это значение угла в радианах. Чтобы воспользоваться этой формулой, нужно знать значение косинуса угла и выполнить несколько простых математических операций.
Например, если мы знаем, что косинус угла равен 0.5, то мы можем использовать формулу для нахождения синуса:
sin(x) = √(1 - cos^2(x))
sin(x) = √(1 - 0.5^2)
sin(x) = √(1 - 0.25)
sin(x) = √(0.75)
sin(x) ≈ 0.866
Таким образом, синус угла, косинус которого равен 0.5, приближенно равен 0.866.
Как найти синус по косинусу формула
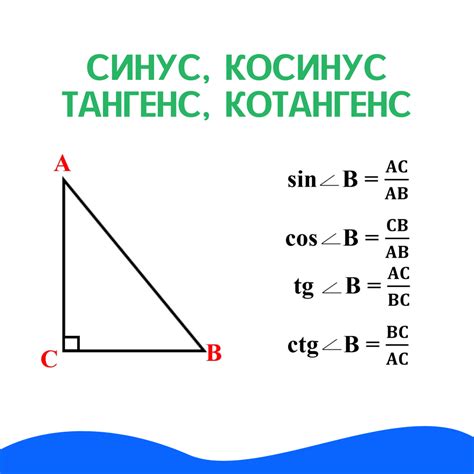
Синус и косинус определены на единичной окружности. Для нахождения синуса по заданному косинусу нужно воспользоваться формулой в помощью связи двух функций:
- Установите значение косинуса, для которого вы хотите найти значение синуса.
- Примените формулу: синус = корень(1 - косинус^2). Эта формула основана на тригонометрической идентичности синуса и косинуса.
- Вычислите значение выражения с использованием калькулятора или программы для работы с математическими функциями.
Например, если известно, что косинус равен 0.5, то можно использовать формулу и найти синус:
синус = корень(1 - 0.5^2) = корень(1 - 0.25) = корень(0.75) ≈ 0.866
Таким образом, синус для косинуса 0.5 равен примерно 0.866.
Зная формулу и применяя ее, вы можете легко находить значение синуса по заданному косинусу.
Шаги и примеры

Для нахождения синуса по косинусу можно использовать следующую формулу:
- 1. Убедитесь, что у вас есть значение косинуса, которое необходимо использовать для вычисления синуса.
- 2. Проверьте, в какой четверти находится угол соответствующий этому косинусу. Это поможет определить знак синуса.
- 3. Используйте тригонометрическое тождество sin^2(x) + cos^2(x) = 1, чтобы найти синус. Зная значение косинуса и знак синуса, вы сможете выразить синус через косинус и решить уравнение.
- 4. Ответом будет синус, который соответствует заданному косинусу и углу в нужной четверти.
Вот пример, чтобы проиллюстрировать процесс:
Допустим, у нас есть значение косинуса cos(x) = 0.5 и мы хотим найти синус sin(x).
- 1. Мы видим, что косинус положителен и меньше 1, поэтому угол будет находиться в первой или четвертой четвертях. Мы также знаем, что косинус равен стороне прилегающей к углу дуги большей гипотенузы.
- 2. Используя тождество, мы можем записать: sin^2(x) + cos^2(x) = 1. Подставляя значение косинуса в уравнение, получаем: sin^2(x) + 0.5^2 = 1.
- 3. Решим это уравнение: sin^2(x) = 1 - 0.5^2 = 1 - 0.25 = 0.75. Отсюда следует, что sin(x) = √(0.75).
- 4. Поскольку у нас есть положительное значение косинуса, мы знаем, что синус будет положительным. Таким образом, ответ будет sin(x) = √(0.75) ≈ 0.866.
Таким образом, синус угла, при котором косинус равен 0.5, примерно равен 0.866.
Формула для вычисления синуса по косинусу

Формула для вычисления синуса по косинусу выглядит следующим образом:
sin(x) = √(1 - cos^2(x))
где x - угол, а cos(x) - значение косинуса этого угла.
Прежде чем использовать эту формулу, необходимо убедиться, что значение косинуса находится в допустимом диапазоне. Косинус может принимать значения от -1 до 1.
Пример:
- Пусть дано: cos(x) = 0.5
- Найдем синус по формуле: sin(x) = √(1 - cos^2(x))
- sin(x) = √(1 - 0.5^2)
- sin(x) = √(1 - 0.25)
- sin(x) = √0.75
- sin(x) ≈ 0.866
Таким образом, синус угла, косинус которого равен 0.5, примерно равен 0.866.
Шаг 1: Найдите значение косинуса

Прежде чем мы сможем найти значение синуса по косинусу, нам нужно найти изначальное значение косинуса. Для этого вы можете использовать таблицы значений тригонометрических функций или использовать калькулятор, который поддерживает тригонометрические функции.
Если вы рассматриваете задачу нахождения косинуса определенного угла, удостоверьтесь, что ваш калькулятор настроен на использование градусов или радианов, в зависимости от того, какой формат угла задан в задаче.
Если вам дано значение косинуса в виде десятичной дроби или в процентах, вы можете использовать обратные функции косинуса, такие как "acos" в математических функциях вашего языка программирования или встроенные функции в калькуляторе.
После того, как вы найдете значение косинуса, запишите его для последующих вычислений.
Шаг 2: Используйте формулу для вычисления синуса
После получения значения косинуса, вы можете использовать простую формулу для вычисления значения синуса. В математике существует специальная соотношение между значениями синуса и косинуса, и вы можете использовать его для расчета.
Формула для вычисления синуса по косинусу выглядит следующим образом:
| Формула для синуса | Значение синуса |
|---|---|
| sin(x) = sqrt(1 - cos^2(x)) | Результат вычисления синуса |
Чтобы найти синус по косинусу, вам нужно возвести значение косинуса в квадрат и вычесть его из единицы. Затем возьмите квадратный корень полученного значения и вы получите итоговое значение синуса.
Например, если у вас есть косинус 0.5, сначала возводите его в квадрат: 0.5^2 = 0.25. Затем отнимите это значение от единицы: 1 - 0.25 = 0.75. Наконец, возьмите квадратный корень этого значения: sqrt(0.75) ≈ 0.866. Таким образом, синус косинуса 0.5 примерно равен 0.866.
Использование данной формулы позволит вам быстро и легко вычислить значение синуса по заданному значению косинуса.