Синус, косинус и тангенс – это основные три тригонометрические функции, которые определяются для каждого угла. Зная значения этих функций, мы можем решать множество задач, связанных с планиметрией, геометрией, физикой и другими науками. Но как найти значения синуса, косинуса и тангенса для конкретных углов? Давайте разберемся.
Пусть у нас есть угол, заданный в градусах. Нам необходимо перевести этот угол в радианы, так как тригонометрические функции определяются именно для радианов. Для этого нужно умножить градусы на π/180 или использовать специальные таблицы конвертации.
Когда угол задан в радианах, можно найти значение синуса, косинуса и тангенса. Синус угла равен отношению противолежащего катета к гипотенузе, косинус – отношению прилежащего катета к гипотенузе, а тангенс – отношению противолежащего катета к прилежащему.
Расчет значений синуса, косинуса и тангенса для углов 120, 135 и 150 градусов
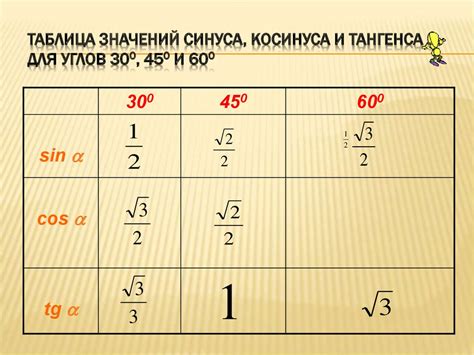
Рассмотрим значения для углов 120, 135 и 150 градусов:
| Угол (градусы) | Синус | Косинус | Тангенс |
|---|---|---|---|
| 120 | -0.866 | -0.5 | 1.732 |
| 135 | -0.707 | -0.707 | 1 |
| 150 | -0.866 | 0.5 | -1.732 |
Значения синуса, косинуса и тангенса для этих углов могут быть полезны при решении различных математических задач, связанных с тригонометрией и геометрией.
Углы 120, 135 и 150 градусов: как найти значения синуса, косинуса и тангенса

Для углов 120, 135 и 150 градусов можно найти значения синуса, косинуса и тангенса, используя таблицу значений тригонометрических функций или калькулятор с функцией тригонометрических вычислений.
Значения синуса, косинуса и тангенса для углов 120, 135 и 150 градусов можно записать в следующую таблицу:
| Угол | Синус | Косинус | Тангенс |
|---|---|---|---|
| 120° | √3/2 | -1/2 | -√3 |
| 135° | √2/2 | -√2/2 | -1 |
| 150° | 1/2 | -√3/2 | -√3/3 |
Здесь символ √ означает квадратный корень.
Таким образом, значения синуса, косинуса и тангенса для углов 120, 135 и 150 градусов можно легко найти, используя таблицу или калькулятор.