Синус наименьшего угла прямоугольного треугольника является одним из основных элементов геометрии. Он позволяет решать различные задачи, связанные с треугольниками, включая нахождение длин сторон, площадей и углов. Но прежде чем объяснить, как найти синус наименьшего угла, давайте освежим память и вспомним основные понятия и определения.
Прямоугольный треугольник – это треугольник, у которого один из углов равен 90 градусов. Сторону, противолежащую прямому углу, называют гипотенузой, а две другие стороны – катетами.
Синус угла – это отношение противоположной стороны к гипотенузе треугольника. В прямоугольном треугольнике наименьший угол всегда лежит между одним из катетов и гипотенузой. Поэтому для нахождения синуса наименьшего угла нам достаточно знать длину противоположного катета и гипотенузы.
Как найти синус прямоугольного треугольника?
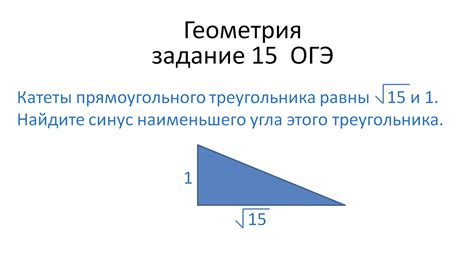
Синус прямоугольного треугольника представляет собой отношение длины противоположного катета к гипотенузе.
Для того чтобы найти синус прямоугольного треугольника, нужно знать длину противоположего катета и гипотенузы. Формула для нахождения синуса выглядит следующим образом:
| Формула | Описание |
|---|---|
| синус угла | противоположный катет / гипотенуза |
| sin(α) | a / c |
Где:
- sin(α) - синус угла
- a - длина противоположего катета
- c - длина гипотенузы
При наличии этих данных, подставляем их в формулу и получаем значение синуса прямоугольного треугольника.
Например, у нас есть прямоугольный треугольник с противоположим катетом a = 3 и гипотенузой c = 5. Подставляя эти значения в формулу, мы получаем:
sin(α) = 3 / 5 ≈ 0.6
Таким образом, синус угла примерно равен 0.6.
Найденное значение синуса может быть использовано для решения различных задач, связанных с прямоугольным треугольником, например, нахождение других тригонометрических функций (косинуса, тангенса и т.д.), а также решения уравнений и задач геометрии.
Определение наименьшего угла треугольника
При рассмотрении прямоугольного треугольника можно определить наименьший угол с помощью основных свойств и формул. Для этого следует запомнить следующие правила:
1. Определение острого угла:
В прямоугольном треугольнике имеется один острый угол, он находится противоположно гипотенузе. Активно использование тригонометрических функций позволяют определить синус острого угла.
2. Использование теоремы Пифагора:
Теорема Пифагора утверждает, что квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длины катетов. Используя данную теорему, можно определить длину каждой стороны треугольника и затем рассчитать все углы.
3. Вычисление синуса наименьшего угла:
Для определения синуса наименьшего угла прямоугольного треугольника, можно использовать соотношение между гипотенузой и катетом, либо использовать тригонометрический радиус или таблицу тригонометрических значений.
Важно: для определения наименьшего угла треугольника, требуется знание всех сторон и длин противоположных углов.
Расчет длины противоположенной стороны
Для нахождения синуса наименьшего угла прямоугольного треугольника необходимо знать длину противоположенной этому углу стороны. Расчет этой стороны осуществляется по формуле:
a = c * sin(A)
где a - длина противоположенной стороны, c - гипотенуза треугольника, A - наименьший угол прямоугольного треугольника.
Формула основывается на том, что синус угла равен отношению противоположенной стороны к гипотенузе.
Таким образом, для нахождения синуса наименьшего угла прямоугольного треугольника необходимо знать значение гипотенузы и значение наименьшего угла, а после применить указанную формулу для расчета длины противоположенной стороны.
Вычисление синуса наименьшего угла
Синус наименьшего угла прямоугольного треугольника можно вычислить с использованием тригонометрических функций.
Для начала, определим наименьший угол прямоугольного треугольника. В прямоугольном треугольнике гипотенуза, обозначенная как c, является самой длинной стороной, а катеты, обозначенные как a и b, являются более короткими сторонами. Углы прямоугольного треугольника обозначаются как α, β и γ, сумма которых равна 90 градусам.
Наименьший угол прямоугольного треугольника можно найти, используя тригонометрическую функцию арктангенс (или инверсную тангенс) и соотношение тангенса угла к соответствующей стороне треугольника.
Формула для вычисления синуса наименьшего угла:
- Вычислить тангенс наименьшего угла с помощью формулы: тангенс наименьшего угла = a / b или b / a.
- Вычислить синус наименьшего угла с помощью формулы: синус наименьшего угла = тангенс наименьшего угла / √(1 + (тангенс наименьшего угла)²).
Теперь мы знаем, как вычислить синус наименьшего угла прямоугольного треугольника. Этот метод может быть полезен, когда вам нужно найти синус наименьшего угла для решения геометрических или технических задач.