Синус и тангенс - это две из основных тригонометрических функций, которые широко используются в математике, физике и других науках. Изучение этих функций позволяет лучше понять связь между углами и сторонами в треугольнике
Часто возникает необходимость найти синус через тангенс, особенно при решении тригонометрических уравнений или построении графиков функций. Для этого существует специальная формула, которая позволяет вычислить синус, зная значение тангенса угла.
Формула для нахождения синуса через тангенс выглядит следующим образом: синус угла = тангенс угла / √(1 + тангенс^2 угла). С помощью этой формулы можно точно вычислить значение синуса, зная значение тангенса угла.
Процесс вычисления синуса через тангенс является достаточно простым. Достаточно подставить значение тангенса угла в формулу и выполнить несколько математических действий. Полученное значение синуса будет точным и полезным для решения задач и построения графиков.
Использование тангенса для вычисления синуса: формула и методы

Формула для нахождения синуса через тангенс выглядит следующим образом:
| Формула для нахождения синуса через тангенс: |
|---|
| sin(x) = tan(x) / sqrt(1 + tan^2(x)) |
Для вычисления синуса по этой формуле необходимо знать значение тангенса угла x. Если известно значение тангенса, его можно подставить в формулу и получить значение синуса.
Существуют также более быстрые и эффективные методы для вычисления синуса через тангенс, такие как использование таблиц или специализированных алгоритмов. Например, можно использовать таблицу значений тангенса и соответствующих им значений синуса, чтобы найти приближенное значение синуса по известному тангенсу. Также некоторые программы и калькуляторы могут предоставлять встроенные функции для вычисления синуса по тангенсу.
Использование тангенса для вычисления синуса может быть полезным, например, при решении задач, связанных с треугольниками или круговыми функциями. Зная значение тангенса определенного угла, можно легко вычислить его синус и использовать полученный результат для дальнейших вычислений.
Что такое тангенс и синус
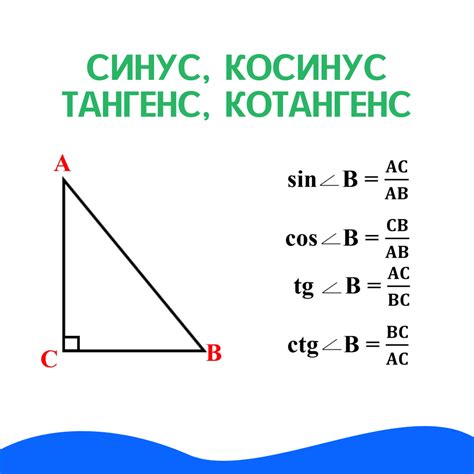
Синус (обозначается как sin) - это также тригонометрическая функция, которая определяется как отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.
Тангенс и синус являются связанными функциями, поскольку они позволяют определить друг друга. Для этого существуют соответствующие формулы. Например, чтобы найти синус через тангенс, можно воспользоваться формулой:
sin(x) = tg(x) / √(1 + tg^2(x))
где x - угол, а tg(x) - значение тангенса угла x. Эта формула позволяет вычислить значение синуса, используя известное значение тангенса.
Таким образом, зная определение и формулы для тангенса и синуса, можно легко взаимно вычислять эти функции и использовать их в решении различных математических задач.
Формула вычисления синуса через тангенс
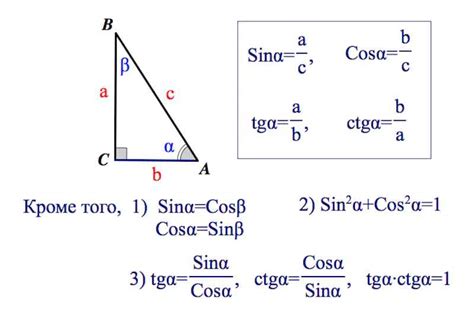
Формула вычисления синуса через тангенс имеет следующий вид:
- sin(θ) = tan(θ) / √(1 + tan²(θ))
Где sin(θ) обозначает синус угла θ, tan(θ) обозначает тангенс угла θ, а √ символизирует операцию извлечения квадратного корня.
Эта формула позволяет найти синус угла, если известно значение его тангенса. Она основывается на связи между различными тригонометрическими функциями и может быть использована для решения различных задач в геометрии, физике и инженерии.
Пример вычисления синуса через тангенс:
- Пусть дано значение тангенса θ = 0.8.
- Подставляем значение в формулу: sin(θ) = 0.8 / √(1 + 0.8²).
- Вычисляем значение в знаменателе: 1 + 0.8² = 1 + 0.64 = 1.64.
- Извлекаем квадратный корень из знаменателя: √1.64 ≈ 1.28.
- Подставляем коэффициенты в формулу: sin(θ) ≈ 0.8 / 1.28 ≈ 0.625.
- Ответ: sin(θ) ≈ 0.625.
Таким образом, используя формулу вычисления синуса через тангенс, можно определить значение синуса угла, зная его тангенс.
Рекомендации и способы использования вычисления синуса через тангенс
Формула вычисления синуса через тангенс предоставляет удобный способ определения значения синуса угла, основываясь на известном значении тангенса угла. Однако, прежде чем использовать эту формулу, важно следовать определенным рекомендациям и знать способы вычисления тангенса.
Во-первых, чтобы правильно использовать формулу вычисления синуса через тангенс, необходимо иметь значение тангенса угла. Для этого можно воспользоваться таблицей значений тангенса или использовать калькулятор с возможностью вычисления тангенса.
Во-вторых, формулу можно использовать как для вычисления синуса углов, находящихся в первом и втором квадрантах, так и для углов, находящихся в третьем и четвертом квадрантах. Для углов в первом и втором квадрантах значение синуса будет положительным, а для углов в третьем и четвертом квадрантах - отрицательным.
Чтобы вычислить значение синуса через тангенс, необходимо использовать следующую формулу:
sin(x) = tan(x) / √(1 + tan^2(x))
Где sin(x) - значение синуса угла x, а tan(x) - значение тангенса угла x.
После вычисления значения синуса через тангенс, можно использовать это значение в различных задачах и вычислениях, которые требуют наличия значения синуса. Например, в геометрии можно использовать вычисленное значение синуса для определения длины стороны треугольника или высоты по формуле sin(x) = h / c, где h - высота, а c - гипотенуза.
Таким образом, вычисление синуса через тангенс является полезным инструментом, который позволяет получить значение синуса угла на основе известного значения тангенса и использовать его в различных вычислениях и задачах.