Математика предлагает нам множество функций, которые помогают в решении различных задач. Одной из таких функций является синус. Отвечая на вопрос о том, как найти синус по тангенсу, мы получаем возможность расширить свои знания в этой области.
Синус и тангенс являются тригонометрическими функциями, которые связаны друг с другом. Тангенс определяется как отношение противолежащего катета к прилежащему в прямоугольном треугольнике, а синус - как отношение противолежащего катета к гипотенузе. Имея значение тангенса, мы можем найти синус с помощью нескольких методов.
Первый метод основан на определении синуса через тангенс. Для этого используется формула: синус равен отношению тангенса к корню из суммы единицы и квадрата тангенса. Эта формула позволяет найти значение синуса, зная значение тангенса. Такой подход может быть полезен при проведении различных расчетов и измерений в физике, инженерии и других науках.
Методы нахождения синуса по тангенсу

Первый метод основывается на треугольнике, в котором известен тангенс угла. Если представить себе прямоугольный треугольник, в котором один из углов равен искомому углу, а противолежащий катет равен 1, то тангенс этого угла будет равен отношению противолежащего катета к прилежащему. Зная тангенс, можно использовать теорему Пифагора для нахождения гипотенузы треугольника. И синус угла равен отношению противолежащего катета к гипотенузе.
Второй метод заключается в использовании тригонометрической идентичности. Известно, что синус угла равен отношению противолежащего катета к гипотенузе. А тангенс угла равен отношению противолежащего катета к прилежащему. Используя тригонометрическую идентичность sin^2(x) + cos^2(x) = 1, можно выразить гипотенузу через синус и косинус угла. Затем подставить эту формулу в тангенс и выразить синус угла через тангенс и косинус.
Третий метод основан на использовании таблиц тригонометрических функций. В таблицах можно найти значения синуса и тангенса для различных углов. Если известен тангенс угла, можно найти значение синуса, находя ближайшее значение тангенса в таблице и соответствующий ему синус.
У каждого метода есть свои достоинства и применение в зависимости от задачи и известных данных. Используя любой из этих методов, можно найти значение синуса по известному тангенсу угла.
Раздел 1: Использование треугольника для вычисления синуса
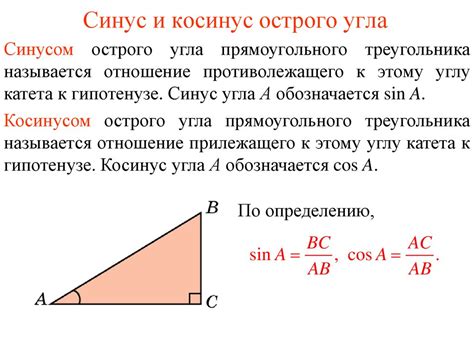
Процесс вычисления синуса с помощью треугольника основан на определении синуса в прямоугольном треугольнике как отношения длины противолежащего углу катета к длине гипотенузы.
Формула для вычисления синуса угла A в прямоугольном треугольнике:
sin(A) = противолежащая / гипотенуза
Помните, что противолежащая сторона - это сторона, напротив угла, синус которого необходимо найти, а гипотенуза - это наибольшая сторона треугольника, противолежащая прямому углу.
Например, если известно, что противолежащая сторона равна 4 и гипотенуза равна 5, можно вычислить синус угла A:
sin(A) = 4 / 5 = 0.8
Таким образом, синус угла A равен 0.8.
Использование треугольника для вычисления синуса является одним из основных методов в тригонометрии и позволяет найти значение этой функции с высокой точностью.
Раздел 2: Применение тригонометрических тождеств для расчета синуса

Для расчета синуса по тангенсу можно использовать тригонометрические тождества, которые связывают значения синуса, косинуса и тангенса для одного и того же угла.
Одним из таких тождеств является соотношение:
- Синус угла равен отношению противолежащего катета к гипотенузе треугольника, а значит, можно воспользоваться соотношениями:
- Синус угла равен косинусу дополнительного угла:
sin(π/2 - α) = cos(α). - Или можно использовать второе тригонометрическое тождество:
sin(α) = √(1 - cos²(α)).
На практике это означает, что если известен тангенс угла α, то можно воспользоваться одним из тождеств и найти синус данного угла.
Например, если дано, что тангенс угла α равен 0.5, то сначала найдем косинус угла α, используя тождество sin(π/2 - α) = cos(α). Затем, подставим найденное значение косинуса во второе тождество, чтобы найти значение синуса: sin(α) = √(1 - cos²(α)).
Таким образом, применение тригонометрических тождеств позволяет легко и точно вычислить синус по известному значению тангенса.
Раздел 3: Использование таблицы значений тангенса и синуса
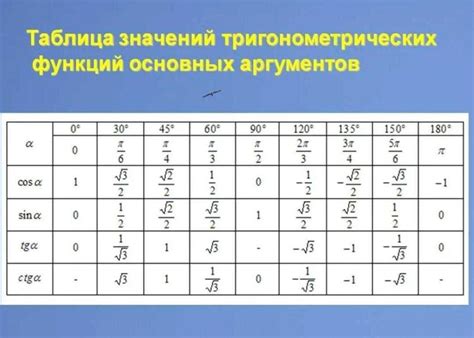
В таблице приводятся значения тангенса и соответствующие им значения синуса. Для нахождения синуса по заданному тангенсу необходимо найти в таблице значение тангенса и соответствующее ему значение синуса. Затем можно использовать найденное значение синуса в дальнейших расчетах или анализе задачи.
Таблица значений тангенса и синуса может быть найдена онлайн или в учебном пособии по математике. С ее помощью можно быстро находить значения синуса и тангенса для различных заданных углов, что значительно упрощает работу с данными функциями.
Однако стоит отметить, что использование таблицы значений тангенса и синуса не является точным методом нахождения значений. В таблице могут быть указаны значения только для определенного диапазона углов, и при необходимости нахождения синуса для угла, выходящего за этот диапазон, придется применить другие методы.
Тем не менее, таблица значений тангенса и синуса является полезным инструментом для быстрого вычисления значений этих функций и может быть использована в ряде практических задач, связанных с математикой и физикой.
Раздел 4: Примеры решения задач на нахождение синуса по тангенсу

Для нахождения синуса по тангенсу используется соотношение, основанное на определении тангенса и синуса.
Пример 1:
Дано: тангенс угла α = 1.5
Найти: синус угла α
Решение:
Из определения тангенса, получаем:
тангенс α = противолежащий катет / прилежащий катет
1.5 = противолежащий катет / прилежащий катет
Пусть противолежащий катет равен 1.5х, тогда прилежащий катет равен x. Тогда:
1.5 = 1.5х / х
1.5 = 1.5
Таким образом, синус угла α равен 1.
Пример 2:
Дано: тангенс угла β = 0.75
Найти: синус угла β
Решение:
Из определения тангенса, получаем:
тангенс β = противолежащий катет / прилежащий катет
0.75 = противолежащий катет / прилежащий катет
Пусть противолежащий катет равен 0.75х, тогда прилежащий катет равен x. Тогда:
0.75 = 0.75х / х
0.75 = 0.75
Таким образом, синус угла β равен ≈ 0.866.
Пример 3:
Дано: тангенс угла γ = -2
Найти: синус угла γ
Решение:
Из определения тангенса, получаем:
тангенс γ = противолежащий катет / прилежащий катет
-2 = противолежащий катет / прилежащий катет
Пусть противолежащий катет равен -2х, тогда прилежащий катет равен x. Тогда:
-2 = -2х / х
-2 = -2
Таким образом, синус угла γ равен -1.