В математике синус и косинус являются двумя основными тригонометрическими функциями, которые широко используются для решения различных задач. Знание этих функций позволяет решать уравнения, выполнять геометрические построения и проводить дальнейшие исследования в различных областях науки.
Синус и косинус взаимно связаны между собой. Как найти синус через косинус? Существует несколько простых способов, которые помогут вам справиться с этой задачей.
Один из методов - использование известного тригонометрического тождества: синус²(α) + косинус²(α) = 1. Пользуясь этим равенством, вы можете найти синус от угла α, зная его косинус. Просто возьмите квадратный корень из разности единицы и косинуса, и получите значение синуса.
Что такое тригонометрические функции?

Основные тригонометрические функции включают синус (sin), косинус (cos), тангенс (tan), котангенс (cot), секанс (sec) и косеканс (csc). Каждая из этих функций имеет свой уникальный набор свойств и используется для решения различных задач.
Например, синус (sin) угла в треугольнике определяется отношением противолежащей стороны к гипотенузе. Косинус (cos) угла определяется отношением прилежащей стороны к гипотенузе. Тангенс (tan) угла определяется отношением противолежащей стороны к прилежащей стороне, а котангенс (cot) - отношением прилежащей стороны к противолежащей.
Тригонометрические функции имеют множество свойств и идентичностей, которые позволяют проводить различные преобразования и решать тригонометрические уравнения. Также они были основой для развития различных методов и техник, используемых при работе с углами и треугольниками.
| Тригонометрическая функция | Определение |
|---|---|
| Синус (sin) | Противолежащая сторона / Гипотенуза |
| Косинус (cos) | Прилежащая сторона / Гипотенуза |
| Тангенс (tan) | Противолежащая сторона / Прилежащая сторона |
| Котангенс (cot) | Прилежащая сторона / Противолежащая сторона |
| Секанс (sec) | Гипотенуза / Прилежащая сторона |
| Косеканс (csc) | Гипотенуза / Противолежащая сторона |
Чему равен синус угла?

Синус угла представляет собой тригонометрическую функцию, которая описывает отношение длины противолежащего катета к гипотенузе прямоугольного треугольника.
Для любого угла, синус представляет отношение высоты точки на единичной окружности к ее радиусу. Это можно представить как значение координаты y точки на окружности.
Синус угла может быть вычислен с помощью известной формулы:
sin(α) = противолежащий катет / гипотенуза
Синус угла может принимать значения от -1 до 1 включительно. Нулевое значение синуса соответствует углу 0°, а максимальное значение равно 1 и соответствует углу 90°.
Как рассчитать косинус угла?

Существует несколько методов расчета косинуса угла:
- Таблица иллюстрирующая значения косинуса углов от 0 до 90 градусов, которую можно легко найти в учебниках по тригонометрии.
- Использование калькулятора, который имеет функцию для расчета тригонометрических функций.
- Приближенный метод с использованием формулы Тейлора или других математических аппроксимаций.
Самый простой метод – использование таблицы косинусов. В таблице косинусов указываются значения косинуса для различных углов, а пользователь может найти нужное значение по углу из таблицы.
Второй метод – использование калькулятора. Многие современные калькуляторы имеют функцию для расчета тригонометрических функций. Для расчета косинуса нужно ввести значение угла и нажать соответствующую кнопку.
Третий метод – наиболее точный, но требует знания математических формул и навыков работы с ними. Например, можно использовать формулу Тейлора для расчета косинуса. Этот метод часто используется при программировании или в математических расчетах, когда нужна высокая точность.
Итак, рассчитать косинус угла можно с помощью таблицы, калькулятора или математических формул. Выбор метода зависит от потребностей и точности, которую требуется достичь в расчете.
Определение синуса через косинус

Для определения синуса через косинус можно воспользоваться тригонометрическим тождеством, известным как "тангенсальное" тождество:
sin(x) = √(1 - cos^2(x))
Используя это тождество, можно легко определить значение синуса для любого угла по известному значению косинуса. Для этого необходимо:
1. Найти значение косинуса (cos) для заданного угла.
2. Подставить найденное значение в формулу "тангенсального" тождества и вычислить значение синуса (sin).
Такой способ определения синуса через косинус может быть полезен при решении задач, связанных с тригонометрией, физикой или инженерными расчетами. Он позволяет использовать известные значения косинуса для нахождения соответствующих значений синуса.
Почему углы синуса и косинуса связаны?

Угол синуса (sin) определяется как отношение противолежащей стороны к гипотенузе треугольника, тогда как угол косинуса (cos) определяется как отношение прилежащей стороны к гипотенузе. Таким образом, эти две функции связаны напрямую со свойствами исходного треугольника.
Связь между углами синуса и косинуса выражается с помощью тригонометрического тождества Пифагора:
- sin^2(α) + cos^2(α) = 1
Это тождество описывает, что квадраты синуса и косинуса угла α, при сложении, равны единице. Из этого следует, что синус и косинус являются взаимно-обратными функциями друг друга.
Также, с помощью связи между синусом и косинусом, можно найти одну функцию через другую. Например, с помощью свойства: sin(α) = √(1 - cos^2(α)), можно найти значение синуса, если известно значение косинуса угла α.
Тригонометрические функции синуса и косинуса широко используются в различных областях науки и техники, таких как физика, инженерия, компьютерная графика и др. Понимание связи между этими функциями позволяет более эффективно решать различные задачи, связанные с углами и сторонами треугольников.
Простые методы вычисления синуса

Существует несколько простых методов, позволяющих вычислить синус угла, используя значение косинуса и другие тригонометрические отношения:
- Используйте тождество $\sin^2 \theta + \cos^2 \theta = 1$, чтобы найти значение синуса, если известен косинус угла. Синус можно найти, используя формулу $\sin \theta = \sqrt{1 - \cos^2 \theta}$.
- Используйте основное тригонометрическое тождество $\sin \theta = \frac{\tan \theta}{\sqrt{1 + \tan^2 \theta}}$, чтобы вычислить синус, зная тангенс угла.
- Используйте частное тригонометрическое тождество $\sin \theta = \frac{2 \tan \frac{\theta}{2}}{1 + \tan^2 \frac{\theta}{2}}$, чтобы найти синус, если известен половинный угол и его тангенс.
- Используйте таблицы или калькуляторы со встроенными функциями синуса, чтобы получить точное значение синуса угла.
Эти методы позволяют с легкостью вычислить синус угла при известных значениях других тригонометрических функций. При этом важно помнить, что нахождение и использование точных значений может быть критично для определенных задач, поэтому таблицы или калькуляторы могут быть необходимы для получения более точных результатов.
Примечание: В этой статье мы рассмотрели только простые методы для вычисления синуса угла. Существуют и другие более сложные алгоритмы, такие как ряды Тейлора или различные приближения, которые используются для вычисления синуса численно в более точном виде.
Использование таблицы значений для нахождения синуса
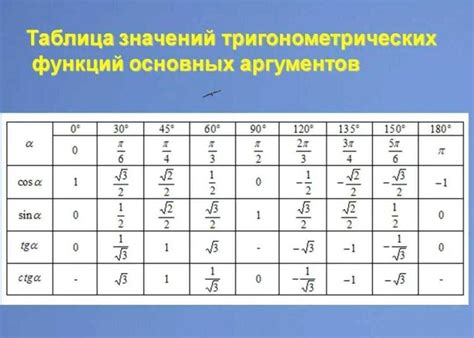
Если вы хотите найти значение синуса угла, но у вас есть только значение косинуса, вы можете использовать таблицу значений для упрощения этой задачи. Таблица значений представляет собой удобный инструмент, который позволяет найти значения тригонометрических функций для различных углов.
Чтобы использовать таблицу значений для нахождения синуса, вам нужно найти значение угла, для которого известно значение косинуса. Затем найдите соответствующее значение синуса в той же строке таблицы. Например, если значение косинуса равно 0,6, найдите в таблице значение синуса, соответствующее этому углу.
Таблица значений готова к использованию, и в ней представлены основные значения синуса и косинуса для различных углов от 0 до 90 градусов. Вы можете использовать эту таблицу для нахождения значения синуса, когда у вас есть только значение косинуса. Просто найдите значение косинуса в таблице и прочтите соответствующее значение синуса в той же строке.
Инструменты для упрощения изучения тригонометрии

Изучение тригонометрии может быть сложным и запутанным процессом, особенно для новичков. Однако, существуют различные инструменты, которые могут помочь вам упростить этот процесс и легче понять основные понятия тригонометрии. Вот несколько из них:
1. Таблицы значений тригонометрических функций: Таблицы синусов, косинусов и других тригонометрических функций позволяют быстро находить значения функций для определенных углов. Они могут быть полезны для решения уравнений, построения графиков и других задач.
2. Тригонометрический круг: Тригонометрический круг – это инструмент, который помогает визуализировать основные понятия тригонометрии, такие как синус, косинус и тангенс. С помощью тригонометрического круга можно быстро определить значения этих функций для любого угла.
3. Калькулятор: Использование калькулятора с тригонометрическими функциями может значительно облегчить выполнение сложных вычислений. Он может быть полезен при нахождении значений функций, решении уравнений и других задач, связанных с тригонометрией.
4. Онлайн ресурсы: В интернете есть множество онлайн ресурсов, которые предлагают объяснения, примеры и задачи по тригонометрии. Они могут быть полезны для самостоятельного изучения тригонометрии и проверки своих знаний.
Все эти инструменты могут помочь вам упростить изучение тригонометрии и повысить ваше понимание основных понятий. Они позволяют быстро находить значения функций, визуализировать графики и выполнять сложные вычисления. Использование этих инструментов совместно с традиционным изучением материала поможет сделать процесс более интересным и эффективным.