Синус - это одна из основных тригонометрических функций, которая широко используется в математике и науках при решении различных задач. Вычисление синуса несложно, если вы знаете правильные формулы и используете некоторые полезные советы.
Существует несколько способов вычисления синуса. Один из самых простых способов - использование тригонометрического круга. Другой способ - использование рядов Тейлора или других соотношений между тригонометрическими функциями. Каждый из этих методов имеет свои преимущества и может быть использован в зависимости от конкретной задачи.
Если вы хотите вычислить синус вручную, вам пригодятся некоторые полезные формулы, которые вы можете использовать. Например, существует формула для вычисления синуса суммы двух углов: sin(x + y) = sin(x) * cos(y) + cos(x) * sin(y). Эта формула может быть очень полезна при вычислении сложных значений синуса.
Также важно помнить о некоторых необходимых советах при вычислении синуса. Во-первых, будьте внимательны с единицами измерения углов. Синус угла может быть отрицательным, если угол лежит во второй или третьей четверти. Если у вас возникают трудности при вычислении синуса, не стесняйтесь использовать тригонометрические таблицы или калькуляторы, которые могут помочь вам получить точные значения.
Изучение синуса

Для понимания синуса необходимо знание основных математических понятий, таких как градусы и радианы, а также умение работать с треугольниками и прямоугольными координатами. Важно понимать, что синус является отношением длины противолежащего катета к гипотенузе прямоугольного треугольника.
Основные формулы для вычисления синуса включают формулу синуса для прямоугольного треугольника, формулу синуса для остроугольного треугольника и ряд Тейлора для приближенного вычисления синуса.
Для вычисления синуса с большей точностью можно использовать табличные значения или специальные программы и калькуляторы. Важно помнить о том, что значения синуса могут быть отрицательными и могут принимать значения в пределах от -1 до 1.
Изучение синуса является важным компонентом обучения математике и наукам, и может пригодиться во многих практических ситуациях, включая решение задач связанных с геометрией, физикой и алгеброй.
Расчет синуса по тригонометрической окружности
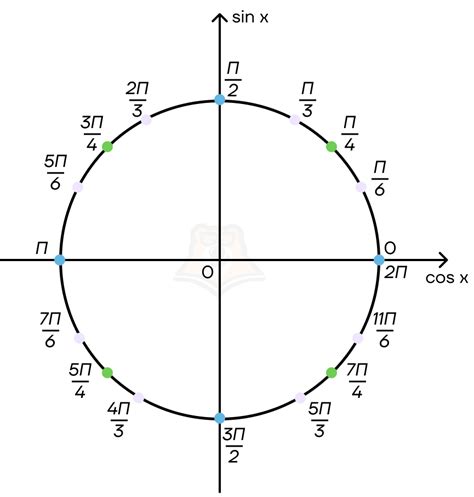
Тригонометрическая окружность - это изображение единичной окружности на координатной плоскости, с центром в начале координат (0,0). На окружности выбирается точка, которая соответствует углу, для которого мы хотим вычислить синус.
Для расчета синуса по тригонометрической окружности необходимо сначала найти точку на окружности, соответствующую значению угла. Затем, выпустить от этой точки перпендикуляр к оси Х и определить точку пересечения его с окружностью.
Зная координаты этой точки пересечения, можно вычислить значение синуса, которое будет равно y-координате этой точки.
| Угол | Точка на окружности | Точка пересечения | Значение синуса |
|---|---|---|---|
| 0 градусов | (1, 0) | (1, 0) | 0 |
| 30 градусов | (1/2, √3/2) | (1/2, √3/2) | 0.5 |
| 45 градусов | (1/√2, 1/√2) | (1/√2, 1/√2) | 0.7071 |
| 60 градусов | (√3/2, 1/2) | (√3/2, 1/2) | 0.866 |
| 90 градусов | (0, 1) | (0, 1) | 1 |
Используя тригонометрическую окружность, можно вычислить синус для любого угла от 0 до 90 градусов. Зная значения синуса для этих углов, можно также вычислить синус для углов, которые больше 90 градусов, используя свойства тригонометрических функций.
Такой способ вычисления синуса позволяет улучшить точность результатов и удобство вычислений, особенно при работе с большими углами и десятичными дробями.
Таблица значений синуса
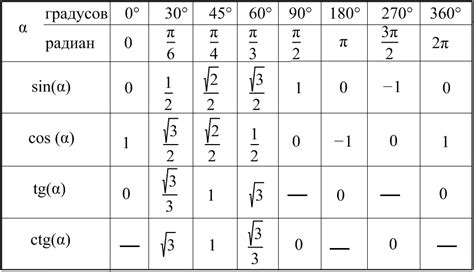
Для вычисления синуса различных углов можно использовать таблицу значений синуса. Такая таблица позволяет быстро получить приближенное значение синуса угла без необходимости использования сложных математических выражений.
Ниже приведена небольшая таблица значений синуса для углов от 0 до 90 градусов:
| Угол (градусы) | Синус |
|---|---|
| 0 | 0 |
| 30 | 0.5 |
| 45 | 0.707 |
| 60 | 0.866 |
| 90 | 1 |
Зная значения синуса для этих углов, можно приближенно вычислить значение синуса для более сложных углов, используя интерполяцию или другие методы аппроксимации.
Важно помнить, что значения в таблице являются приближенными и могут иметь погрешность. Для точных вычислений синуса рекомендуется использовать специализированные математические функции или алгоритмы, доступные в большинстве языков программирования и математических пакетах.
Разложение синуса в ряд

Разложение синуса в ряд представляет собой бесконечную сумму слагаемых, каждое из которых выражено через степени переменной. Формула разложения синуса в ряд имеет вид:
sin(x) = x - (x3/3!) + (x5/5!) - (x7/7!) + ...
В этой формуле каждое слагаемое представляет собой степень переменной, деленную на факториал числа, умноженную на соответствующий знак (- или +).
Чтобы вычислить значение синуса с помощью разложения в ряд, можно взять конечное количество слагаемых или продолжать приближать значение с помощью более точных приближений.
Разложение синуса в ряд широко используется в математике и физике для приближенного вычисления значений синуса в тех случаях, когда нет возможности использовать точные формулы или функции. Однако следует учитывать, что разложение в ряд имеет свои ограничения и приближенные значения могут быть неточными.
Вычисление синуса с помощью калькулятора
Современные калькуляторы обычно уже имеют встроенную функцию для вычисления синуса, что делает процесс получения значения этой функции более простым и быстрым.
Для вычисления синуса с помощью калькулятора следуйте следующим инструкциям:
- Включите калькулятор и убедитесь, что он находится в режиме работы с тригонометрическими функциями.
- Введите угол, для которого нужно вычислить синус, в градусах или радианах, в соответствующее поле.
- Нажмите кнопку "sin" или "sinh" (в зависимости от того, нужно вычислить синус обычный или гиперболический) на калькуляторе.
- Полученное значение синуса будет отображено на дисплее калькулятора.
Если ваш калькулятор не имеет функции для вычисления синуса, вы можете воспользоваться онлайн-калькуляторами, которые доступны на многих веб-сайтах.
Учитывайте, что вычисление синуса может потребоваться в разных единицах измерения (градусы, радианы), поэтому будьте внимательны и проверьте, что ваш калькулятор настроен на правильную систему измерений.
Изучая тему вычисления синуса, помните о применении этой функции в различных областях науки и техники, таких как физика, геометрия, астрономия и других.
Важно знать, как правильно использовать калькулятор для вычисления синуса, чтобы получить точные результаты и избежать ошибок в своих расчетах.
Применяйте данное руководство и успешно вычисляйте синус с помощью калькулятора!
Практические советы по вычислению синуса
- Используйте тригонометрические таблицы: Таблицы синусов позволяют найти значения синуса для различных углов. Они являются надежным и быстрым способом получить нужные значения.
- Используйте ряд Тейлора: Ряд Тейлора является разложением функции синуса в бесконечную сумму. При использовании конечного числа членов ряда можно получить достаточно точное значения синуса.
- Используйте библиотеки программирования: Многие языки программирования предоставляют встроенные функции для вычисления синуса. Использование этих функций обычно является наиболее простым и надежным способом.
Использование комбинации этих методов позволяет получить точные значения синуса для различных углов и способов вычисления. Имейте в виду, что в некоторых случаях могут возникать ошибки округления, поэтому всегда важно учитывать точность вычислений и особенности вашего применения.