Синус, тангенс и котангенс - это основные тригонометрические функции, которые широко используются в математике и физике. Синус угла определяется отношением противолежащего катета к гипотенузе в прямоугольном треугольнике. Тангенс угла - это отношение противолежащего катета к прилежащему катету, а котангенс - это обратное отношение тангенса.
В случае, если известны тангенс и котангенс угла, можно найти синус с помощью тригонометрических тождеств. Для этого следует воспользоваться соотношением: синус угла равен квадратному корню из отношения котангенса к тангенсу.
Математический символ для синуса обозначается символом sin, для тангенса - tg (или tan), а для котангенса - ctg (или cot). Поэтому формула для нахождения синуса угла будет выглядеть следующим образом: sin α = √(ctg α / tg α), где α - угол, для которого мы ищем синус.
Изучите определения тангенса и котангенса

Тангенс угла – это отношение противоположной стороны треугольника к прилежащей стороне. Он обозначается как tg и может быть вычислен по формуле:
tg(угол) = противоположная сторона / прилежащая сторона.
Котангенс угла – это обратное значение тангенса. Он вычисляется как отношение прилежащей стороны к противоположной стороне:
ctg(угол) = прилежащая сторона / противоположная сторона.
Знание определений тангенса и котангенса позволит вам легко вычислять значения этих функций и применять их при решении задач, связанных с треугольниками и углами.
Определите угол, для которого нужно найти синус
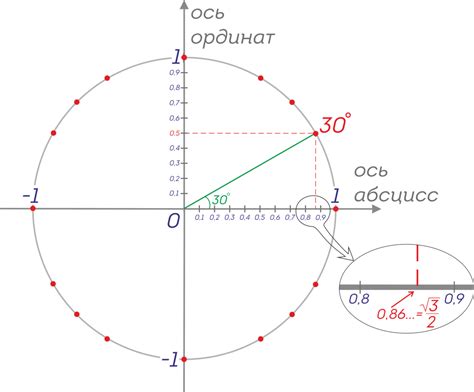
Для нахождения синуса угла необходимо знать значение этого угла. Синус угла можно рассчитать, используя его значение в соответствующей тригонометрической функции.
Если вам известны тангенс и котангенс угла, но неизвестно значение самого угла, необходимо воспользоваться соотношениями:
| Тригонометрическая функция | Формула |
|---|---|
| Тангенс | Тангенс угла равен отношению синуса угла к косинусу угла: |
| tg(θ) = sin(θ) / cos(θ) | |
| Котангенс | Котангенс угла равен обратному отношению тангенса угла: |
| ctg(θ) = 1 / tg(θ) |
Используя эти формулы, вы сможете определить угол, для которого необходимо найти значение синуса.
Выразите тангенс угла через синус и косинус
tg(α) = sin(α) / cos(α)
где α - заданный угол.
Поэтому, чтобы выразить тангенс угла через синус и косинус, нужно поделить синус угла на косинус угла:
tg(α) = sin(α) / cos(α)
Выражение sin(α) / cos(α) эквивалентно тангенсу угла.
Таким образом, тангенс угла может быть выражен через синус и косинус следующим образом:
tg(α) = sin(α) / cos(α)
Выразите котангенс угла через синус и косинус
Выражение котангенса угла через синус и косинус можно получить с помощью тригонометрического тождества:
Тождество: если синус угла равен отношению противолежащего катета к гипотенузе, то косинус угла равен отношению прилежащего катета к гипотенузе.
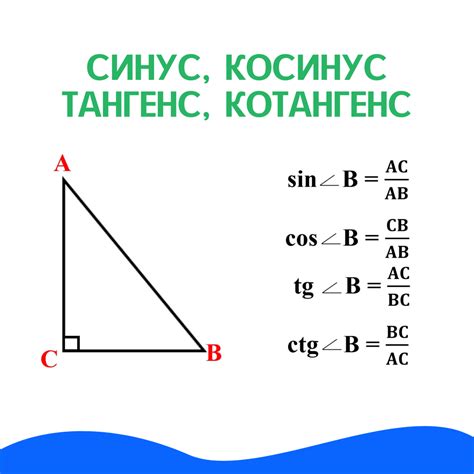
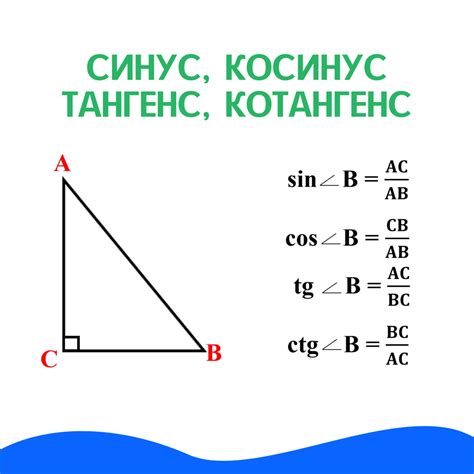
Рассмотрим прямоугольный треугольник ABC, где угол B равен заданному углу, а AC - гипотенуза, AB и BC - катеты.
Из тождества следует, что синус угла B равен отношению катета AC к гипотенузе AB:
sin B = AC / AB
Далее, рассмотрим котангенс угла B, обозначим его как ctg B:
ctg B = 1 / tg B
Используя определение тангенса угла B, получим:
ctg B = 1 / (AC / BC) = BC / AC
Так как верно, что косинус угла B равен отношению катета BC к гипотенузе AB, то мы можем выразить котангенс как отношение косинуса угла B к синусу угла B:
ctg B = BC / AC = cos B / sin B
Итак, котангенс угла B выражается через синус и косинус:
ctg B = cos B / sin B
Используйте формулу для нахождения синуса угла

Для нахождения синуса угла, если известен тангенс, можно использовать следующую формулу:
синус угла = тангенс угла / √(1 + тангенс² угла)
Для нахождения синуса угла, если известен котангенс, можно использовать следующую формулу:
синус угла = 1 / √(1 + котангенс² угла)
Используя эти формулы, вы можете найти синус угла при известном тангенсе или котангенсе и использовать его для дальнейших расчетов.