Синус угла является одной из фундаментальных тригонометрических функций, которая позволяет нам изучать и решать разнообразные задачи, связанные с геометрией и физикой. Знание формулы для нахождения синуса угла по сторонам и площади треугольника может быть полезным при решении геометрических задач и вычислений.
Для нахождения синуса угла по сторонам треугольника можно использовать закон синусов. Формула выглядит следующим образом: sin(A) = a / c, где А - меридиан угла, a - длина противолежащей стороны, c - длина гипотенузы. Зная значения сторон треугольника, мы можем применить данную формулу и вычислить синус угла А.
Если же известна площадь треугольника, можно воспользоваться другой формулой для нахождения синуса угла. Она выглядит следующим образом: sin(A) = 2 * S / (a * b), где А - меридиан угла, S - площадь треугольника, a и b - длины сторон треугольника. Используя данную формулу, мы можем вычислить синус угла А, имея информацию о площади треугольника и длинах его сторон.
Как найти синус угла
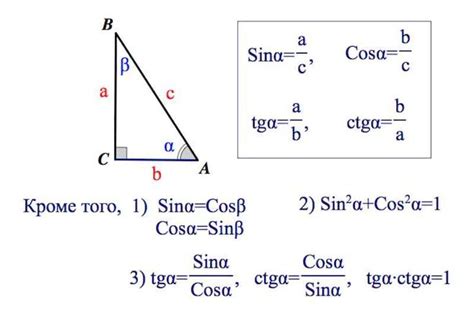
Существует несколько способов вычисления синуса угла в зависимости от данных, которые у вас есть. Один из самых распространенных способов - использование соотношения синуса в прямоугольном треугольнике:
sin(A) = противоположный катет / гипотенуза
Другой способ вычисления синуса угла - использование формулы площади треугольника:
sin(A) = 2 * площадь треугольника / (сторона A * сторона B)
В данной формуле сторона A и сторона B - это длины двух сторон треугольника, а площадь треугольника можно найти с помощью формулы Герона или других методов.
Чтобы найти синус угла по данным сторонам, вам потребуется измерить или найти значения сторон треугольника и воспользоваться соответствующей формулой. Если у вас есть площадь треугольника, вы также можете использовать формулу площади для вычисления синуса угла.
Помните, что синус угла может принимать значения от -1 до 1, и его значение зависит от размера угла. Большие углы имеют большие значения синуса, а маленькие углы - маленькие значения синуса.
Использование синуса угла позволяет решать различные задачи в геометрии, физике, инженерии и других областях науки. Эта функция необходима для вычисления углов, нахождения расстояний и направлений, а также для решения сложных задач трехмерной геометрии.
Формула синуса
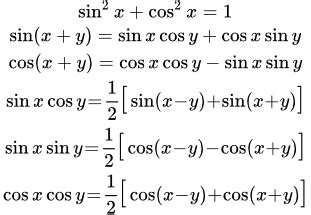
sin(A) = a / c
где:
- sin(A) - синус угла A;
- a - длина противоположной стороны;
- c - длина гипотенузы.
Узнав значения a и c, мы можем использовать формулу синуса, чтобы найти синус угла A. Зная значение синуса, можно также вычислить угол, используя обратную функцию синуса.
Например, если известны стороны прямоугольного треугольника a = 4 и c = 5, синус угла A можно найти следующим образом:
sin(A) = 4 / 5 = 0.8
Таким образом, синус угла A равен 0.8.
Синус угла и стороны треугольника
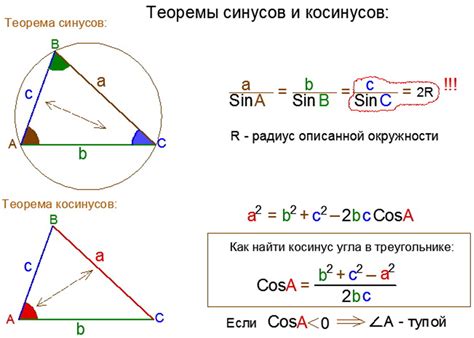
Существует несколько формул, позволяющих найти синус угла по длинам сторон треугольника:
- Формула с использованием площади треугольника:
- Формула с использованием высоты треугольника:
- Формула с использованием радиуса вписанной окружности:
Синус угла можно найти, зная площадь треугольника и длины двух сторон, между которыми расположен искомый угол. Для этого применяется следующая формула:
sin(угол) = 2 * площадь треугольника / (сторона1 * сторона2 * sin(угол между сторонами))
Синус угла можно также найти, зная высоту треугольника, опущенную на сторону, и длины двух других сторон. В таком случае применяется следующая формула:
sin(угол) = (2 * высота треугольника) / (сторона1 + сторона2)
Синус угла можно также найти, зная радиус вписанной окружности и длины двух сторон, в которых лежит искомый угол. Для этого используется следующая формула:
sin(угол) = (2 * радиус вписанной окружности) / (сторона1 * сторона2)
Используя эти формулы, можно находить синусы углов треугольника по длинам его сторон, что позволяет решать различные задачи в геометрии и практических приложениях.
Как найти синус угла по длинам сторон
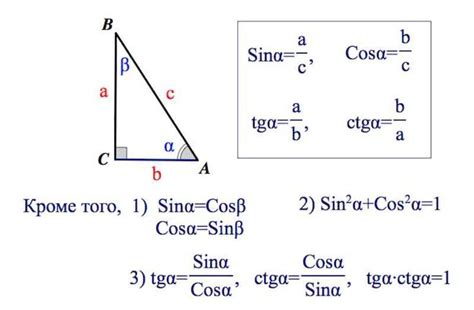
Для того чтобы найти синус угла по длинам сторон треугольника, можно использовать формулу синусов. Формула синусов устанавливает связь между длинами сторон треугольника и синусом угла между этими сторонами.
Формула синусов выглядит следующим образом:
sin(A) = (a / c)
где:
- sin(A) - синус угла A
- a - длина противолежащей стороны углу A
- c - длина гипотенузы треугольника
Для использования этой формулы необходимо знать длину противолежащей стороны и длину гипотенузы треугольника. Подставив эти значения в формулу, можно вычислить синус угла.
Например, если известны длина стороны треугольника, равная 5, и длина гипотенузы, равная 10, мы можем найти синус угла A, подставив значения в формулу:
sin(A) = (5 / 10) = 0.5
Таким образом, синус угла A равен 0.5.
Используя формулу синусов, можно вести расчеты и найди синус угла по длинам сторон треугольника.
Связь синуса угла и площади треугольника
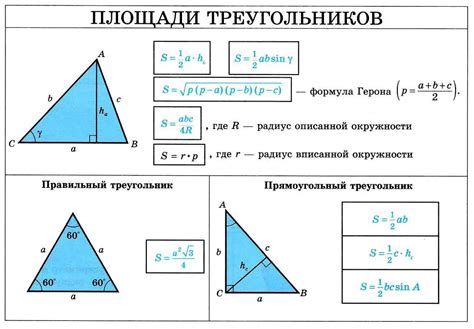
Для прямоугольного треугольника формула выглядит следующим образом:
- Синус угла A = противолежащая сторона / гипотенуза = a / c
- Площадь треугольника = 1/2 * противолежащая сторона * прилежащая сторона = 1/2 * a * b
Для произвольного треугольника введено понятие радиуса вписанной окружности, который определен как отношение площади треугольника к полупериметру:
- Радиус вписанной окружности = Площадь треугольника / Полупериметр треугольника = S / p
Таким образом, синус угла и площадь треугольника взаимосвязаны через длины сторон и радиус вписанной окружности.
Применение этих формул позволяет находить синус угла и площадь треугольника, используя доступные данные о сторонах и периметре треугольника.
Последовательность действий при нахождении синуса угла

Для того чтобы найти синус угла по сторонам или площади, необходимо следовать определенной последовательности действий. Вот шаги, которые нужно выполнить:
- Известные данные: у вас должны быть предоставлены стороны треугольника или его площадь. Эти данные могут быть представлены числами или переменными.
- Определите, какие стороны треугольника известны вам. Если известны две стороны и угол между ними, используйте формулу синусов. Если известны две стороны и противолежащий им угол, используйте формулу площади треугольника.
- Примените соответствующую формулу для нахождения синуса угла. Здесь важно правильно подставить известные данные в формулу.
- Выполните необходимые математические операции, чтобы найти значение синуса угла. Если вы используете калькулятор, убедитесь, что он настроен на градусы.
- Запишите полученное значение синуса угла. Обычно оно представлено в виде десятичной дроби или в виде числа с ограниченным количеством знаков после запятой.
Важно помнить, что для корректного выполнения этих действий необходимо хорошее знание математических основ, включая геометрию и тригонометрию. Также следует проверить свои вычисления и контролировать единицы измерения, чтобы ответ был правильным.
Частные случаи нахождения синуса угла
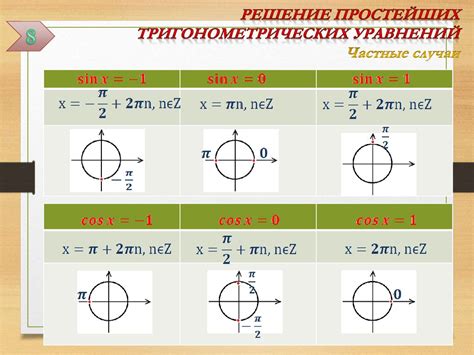
Синус угла, как и другие тригонометрические функции, может быть найден, используя различные данные о треугольнике. В этом разделе мы рассмотрим несколько частных случаев нахождения синуса угла.
| Случай | Условия | Формула |
|---|---|---|
| 1 | Известны две стороны треугольника и угол между ними | sin(A) = (сторона A / сторона C) |
| 2 | Известна одна сторона треугольника и два угла, прилегающих к этой стороне | sin(A) = (сторона A / сторона C) |
| 3 | Известна площадь треугольника и длины двух сторон, образующих угол | sin(A) = (2 * площадь) / (сторона A * сторона C) |
Важно помнить, что значения синуса угла всегда лежат в интервале [-1, 1]. Если результат вашего вычисления не попадает в этот интервал, скорее всего, вы допустили ошибку при решении задачи или использовали неверные данные.
Примеры нахождения синуса угла

Найти синус угла можно, зная отношение противоположного катета к гипотенузе прямоугольного треугольника. Рассмотрим несколько примеров:
Пример 1:
Дано: противоположний катет a = 4, гіпотенуза c = 6
Знайдемо синус кута α:
sin(α) = a / c = 4 / 6 = 2 / 3 ≈ 0.6667
Пример 2:
Дано: противоположний катет a = 5, гіпотенуза c = 13
Знайдемо синус кута β:
sin(β) = a / c = 5 / 13 ≈ 0.3846
Пример 3:
Дано: противоположний катет a = 7, гіпотенуза c = 25
Знайдемо синус кута γ:
sin(γ) = a / c = 7 / 25 = 0.28
Таким чином, знаючи значення противоположного катета та гіпотенузи прямокутного трикутника, можна легко знайти синус відповідного кута.