Синус угла - одно из самых важных понятий в геометрии. Он помогает определить отношение сторон треугольников и других многоугольников, а также найти значения углов. Но что делать, когда требуется найти синус угла в трапеции? В данной статье мы расскажем о методах и формулах, которые помогут вам найти синус угла трапеции без лишних трудностей.
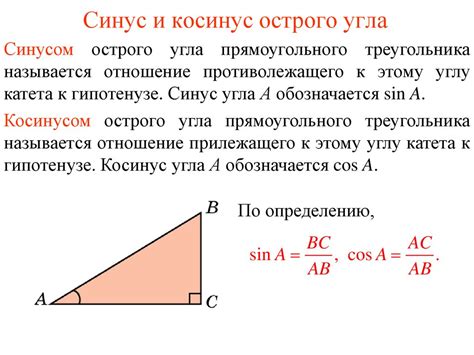
Прежде чем рассмотреть способы нахождения синуса угла трапеции, давайте вспомним основное определение. Синус угла в треугольнике равен отношению противолежащей стороны к гипотенузе. Также существует формула, которая позволяет найти синус угла в треугольнике по значениям двух сторон:
sin A = a / c
Где А - угол в треугольнике, a - противолежащая сторона, c - гипотенуза. Однако, в трапеции углы могут быть разными, и нет однозначной гипотенузы или противолежащей стороны. Поэтому для нахождения синуса угла в трапеции используют другую формулу:
Синус угла трапеции: основные понятия и определения
Для понимания синуса угла трапеции необходимо ознакомиться с некоторыми основными понятиями и определениями:
- Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие стороны непараллельны.
- Вершина трапеции - точка пересечения ее диагоналей.
- Угол трапеции - это угол, образованный двумя соседними сторонами трапеции.
- Синус угла - это тригонометрическая функция, которая отражает отношение длины противоположного катета к гипотенузе в прямоугольном треугольнике. В случае трапеции, синус угла может быть рассчитан с использованием соответствующих сторон и углов.
Для расчета синуса угла трапеции можно использовать следующую формулу:
sin(угол) = противоположная сторона / гипотенуза
Где "противоположная сторона" - это сторона трапеции, противоположная углу, для которого мы хотим рассчитать синус, а "гипотенуза" - это диагональ трапеции, которая проходит через вершину.
Зная значения стороны и диагонали, можно легко рассчитать синус угла трапеции и использовать его для решения задач, связанных с данной геометрической фигурой.
Методы нахождения синуса угла трапеции

1. Использование высоты трапеции: Если известна высота трапеции и один из углов, можно использовать тригонометрический соотношение, а именно синус. Для этого нужно разделить высоту на длину одного из оснований.
2. Использование формулы: Для нахождения синуса угла трапеции можно использовать следующую формулу: синус угла равен разности синусов двух его дополнений. Дополнение угла – это его дополнительный угол, который образуется, если сумма угла и его дополнения равна 90 градусам.
3. Использование тангенса: Метод также основан на тригонометрическом соотношении. Если известна высота трапеции и одно из оснований, можно найти тангенс угла. Затем, используя соотношение тангенса и синуса, можно найти синус угла трапеции.
Важно помнить, что для этих методов требуется знание значений длин оснований и высоты трапеции, а также углов.
Практическое применение: важность синуса угла трапеции в решении геометрических задач
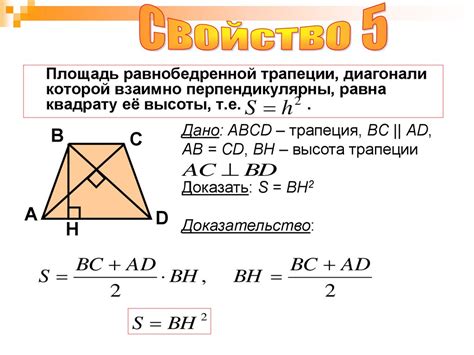
Во-первых, с помощью синуса угла трапеции можно определить площадь фигуры. Зная значение синуса и одного из углов, можно найти длину бокового отрезка и его соотношение с основанием или высотой. С помощью полученных данных можно найти площадь трапеции по формуле, которая включает в себя синус угла.
Во-вторых, синус угла трапеции может быть использован для нахождения длины диагонали трапеции. Для этого необходимо знать значение синуса и одного из углов, а также длины двух сторон. Используя теорему синусов, можно выразить диагональ через длины сторон и синус угла.
Кроме того, синус угла трапеции может быть полезен при нахождении высоты или углов трапеции. Зная значение синуса и одной стороны, можно выразить высоту через длину основания и синус угла. Также можно использовать теорему синусов для нахождения других углов трапеции, если известны значения синуса и сторон.
В общем, синус угла трапеции является полезным инструментом в решении геометрических задач. Он позволяет выразить различные величины через другие, известные данные, и расширяет возможности при решении задач, связанных с трапециями.