Как вычислить сторону треугольника — пошаговое руководство с подробными объяснениями

Вычисление стороны треугольника является одной из основных задач геометрии. Треугольник - это геометрическая фигура, состоящая из трех сторон, которые связаны между собой вершинами. Понимание, как вычислить сторону треугольника, может быть полезно для различных задач, например, для построения дома или решения задач в физике.

Для вычисления стороны треугольника требуется знать значения других сторон либо углов треугольника. Существует несколько способов решить эту задачу, в зависимости от доступных данных. Например, если известны длины двух сторон треугольника и угол между ними, можно применить закон косинусов для вычисления третьей стороны.

Кроме того, существуют специальные типы треугольников, в которых с одной стороны треугольника известен радиус вписанной окружности или радиус описанной окружности, что позволяет найти длину соответствующей стороны треугольника. Другой метод - использование теоремы Пифагора для прямоугольных треугольников, где длины двух сторон известны.

Определение длины стороны треугольника представляет собой важную задачу, которая используется в различных областях знаний. Независимо от способа вычисления, понимание основных методов поможет вам успешно решать проблемы, связанные с треугольниками, и использовать их в реальной жизни.

Как вычислить сторону треугольника: шаг за шагом руководство

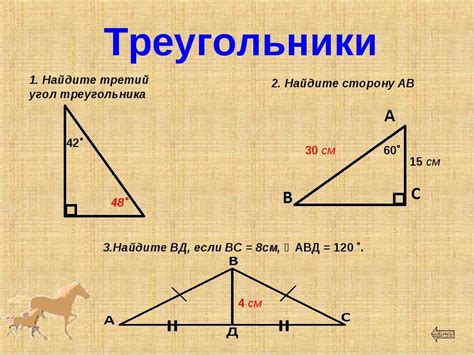
Вычисление сторон треугольника может быть важной задачей в геометрии и математике. Знание длин сторон треугольника помогает решать различные геометрические задачи и применять теоремы.

Для вычисления стороны треугольника нам понадобятся различные данные, которые можно получить из условий задачи или известными формулами.

Если известны длины двух сторон треугольника и угол между ними, то можно воспользоваться теоремой косинусов. Согласно этой теореме, квадрат длины третьей стороны треугольника равен сумме квадратов длин двух других сторон, уменьшенной на удвоенное произведение этих сторон на косинус угла между ними.

Если известны длины трех сторон треугольника, то можно воспользоваться формулой полупериметра и площади. Полупериметр треугольника вычисляется как сумма длин всех его сторон, деленная на 2. Затем, используя формулу Герона, можно вычислить площадь треугольника. Известная площадь треугольника и полупериметр позволяют вычислить длину третьей стороны треугольника.

В некоторых случаях может понадобиться вычислить сторону треугольника, зная только одну сторону и высоту, опущенную на эту сторону. В этом случае можно использовать формулу для вычисления площади треугольника, зная длину одной из сторон и длину высоты, опущенной на эту сторону.

Безусловно, есть и другие методы вычисления сторон треугольника в зависимости от данных, которые имеются. Важно понимать основные геометрические формулы и теоремы, чтобы правильно решать задачи, связанные с вычислением сторон треугольника.

Вычисление стороны треугольника требует точности и внимательности при работе с данными и формулами. Следуя шагам этого руководства и применяя правильные формулы, вы сможете уверенно вычислять стороны треугольников в самых разных задачах.

Используйте теорему Пифагора для вычисления стороны треугольника

Согласно теореме Пифагора, квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов:

c² = a² + b²

Где c - длина гипотенузы, a и b - длины катетов треугольника.

Для вычисления стороны треугольника при помощи теоремы Пифагора, следует знать длины двух других сторон и определить, какую из них является гипотенузой.

Зная длины катетов, можно воспользоваться формулой:

c = √(a² + b²)

Где √ обозначает квадратный корень.

Применяя теорему Пифагора, вы можете вычислить отсутствующую сторону треугольника и получить полную информацию о его геометрических характеристиках.

Используйте тригонометрические функции для нахождения стороны треугольника

Если у вас есть данные о двух сторонах треугольника и угле между ними, вы можете использовать тригонометрические функции для вычисления третьей стороны.

Для вычисления стороны треугольника можно использовать теорему косинусов или теорему синусов.

• Теорема косинусов: $c^2 = a^2 + b^2 - 2ab \cdot \cos(\angle C)$, где $a$ и $b$ - известные стороны треугольника, $C$ - угол между ними, а $c$ - неизвестная сторона.
• Теорема синусов: $\dfrac{a}{\sin(\angle A)} = \dfrac{b}{\sin(\angle B)} = \dfrac{c}{\sin(\angle C)}$, где $a$, $b$ и $c$ - стороны треугольника, а $A$, $B$ и $C$ - соответствующие углы.

Используя одну из этих формул, вы можете выразить неизвестную сторону и решить уравнение, чтобы найти ее значение.

Пример:

1. У вас есть треугольник, у которого известны сторона $a = 5$ и $b = 7$, а угол между ними $C = 60^\circ$.
2. Используя теорему косинусов, мы можем посчитать третью сторону треугольника: $c^2 = 5^2 + 7^2 - 2 \cdot 5 \cdot 7 \cdot \cos(60^\circ)$.
3. Решив это уравнение, мы найдем, что $c^2 = 25 + 49 - 70 \cdot 0.5 = 54$, и, следовательно, $c = \sqrt{54} \approx 7.35$.

Помните, что для использования тригонометрических функций вам может понадобиться знать значения углов в радианах. Если вам даны углы в градусах, вы можете преобразовать их в радианы, умножив на $ \frac{{\pi}}{{180}}$.

Используйте формулу гипотенузы для вычисления стороны треугольника

Для вычисления стороны треугольника можно использовать формулу гипотенузы. Всякий раз, когда вам известны длины двух других сторон треугольника, вы можете использовать эту формулу для определения длины третьей стороны, являющейся гипотенузой.

Формула гипотенузы основана на теореме Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. Таким образом, для вычисления гипотенузы можно воспользоваться следующей формулой:

c = √(a² + b²)

Где:

• c - длина гипотенузы, которую мы хотим найти;
• a и b - длины двух других сторон треугольника, известные нам.

Применение этой формулы очень простое. Замените переменные a и b на известные вам значения длин сторон и выполните вычисления. Результат будет представлять собой длину гипотенузы треугольника.

Например, если у нас есть треугольник со сторонами a = 3 и b = 4, мы можем использовать формулу гипотенузы, чтобы найти длину гипотенузы c. Подставляя значения в формулу, мы получим:

c = √(3² + 4²) = √(9 + 16) = √25 = 5

Итак, длина гипотенузы данного треугольника равна 5.

Теперь, когда вы знакомы с формулой гипотенузы, вы можете легко вычислять длины сторон треугольников, используя этот метод. Убедитесь, что известные вам значения сторон подходят для использования в этой формуле, и у вас получится правильный результат.