Прямоугольные треугольники являются одними из самых распространенных геометрических фигур и часто встречаются в различных задачах и расчетах. Иногда, при работе с данными треугольниками, возникает необходимость найти значения их сторон. Одним из способов решения такой задачи является использование площади треугольника в сочетании с теоремой Пифагора.
Теорема Пифагора утверждает, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов. Это может быть полезно при нахождении сторон треугольника, если дана его площадь.
Для применения этого метода необходимо знать площадь треугольника и одну из его сторон. Мы можем использовать формулу для нахождения площади прямоугольного треугольника, которая зависит от длин его катетов: Площадь = (a * b)/2, где a и b - катеты треугольника. После этого можем использовать также формулу Пифагора для нахождения гипотенузы или другой стороны треугольника.
Формула для нахождения сторон прямоугольного треугольника по площади
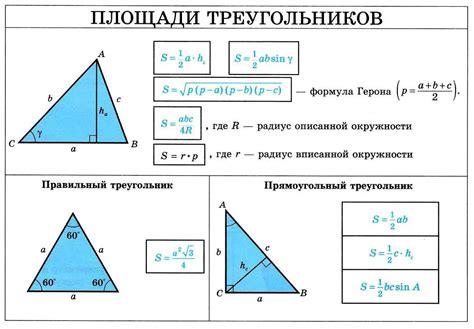
Если известна площадь прямоугольного треугольника и одна из его сторон, то можно найти остальные стороны с использованием специальной формулы.
Формула для нахождения сторон прямоугольного треугольника по площади выглядит следующим образом:
Уравнение: a * b = 2 * S, где "a" и "b" - катеты прямоугольного треугольника, "S" - площадь треугольника.
Чтобы решить это уравнение:
- Введите известные данные: значение площади "S" и одну из сторон треугольника, например "a".
- Для нахождения второй стороны "b" разделите значение площади на первую сторону: b = (2 * S) / a.
Таким образом, с использованием этой формулы вы сможете найти стороны прямоугольного треугольника по известной площади и одной из сторон.
Решение задачи по геометрии

Дано: площадь прямоугольного треугольника равна S.
Требуется: найти длины катетов a и b.
Для решения данной задачи можно воспользоваться формулой для площади прямоугольного треугольника:
S = (a * b) / 2
где a и b - длины катетов треугольника.
Так как задана площадь треугольника S, можно найти значения катетов a и b, применив обратную операцию к формуле площади:
S * 2 = a * b
Итак, для нахождения длин катетов прямоугольного треугольника, необходимо умножить площадь S на 2 и взять квадратный корень полученного значения:
a = √(S * 2)
b = √(S * 2)
Таким образом, для нахождения длин катетов прямоугольного треугольника по заданной площади, достаточно взять квадратный корень от произведения площади на 2.
Пример вычисления и разбор решения

Допустим, у нас есть прямоугольный треугольник со сторонами a, b и гипотенузой c, а также заданная площадь S.
Для нахождения сторон треугольника по площади можно воспользоваться формулой:
S = (a * b) / 2
Также известно, что сторона гипотенузы относится к сторонам a и b по теореме Пифагора:
c^2 = a^2 + b^2
Для решения задачи, сначала найдем стороны a и b через площадь S. Подставим формулу для площади в уравнение Пифагора:
c^2 = a^2 + b^2
c^2 = (2S / b) + b^2
Получившееся уравнение можно решить численными методами или методом пристального взгляда. В данном примере воспользуемся последним и предположим, что b = 1:
c^2 = (2S / 1) + 1^2
Теперь найдем значение стороны c, возведя обе части уравнения в квадрат:
c = sqrt((2S / 1) + 1^2)
Наконец, найдем значение стороны a, подставив полученные значения c и b в уравнение Пифагора:
a = sqrt(c^2 - b^2)
Таким образом, мы нашли все стороны прямоугольного треугольника по заданной площади S и завершили решение задачи.