Определить сумму нескольких векторов по их координатам - довольно простая задача в линейной алгебре. Векторы являются основными объектами изучения векторной алгебры и широко применяются во многих областях науки и техники.
Каждый вектор можно представить с помощью своих координат в пространстве. В случае трехмерного пространства вектор задается тремя числами, которые соответствуют его координатам по осям x, y и z. Для нахождения суммы трех векторов нужно просто сложить соответствующие координаты каждого вектора.
Пусть у нас есть три вектора A, B и C с координатами (Ax, Ay, Az), (Bx, By, Bz) и (Cx, Cy, Cz) соответственно. Чтобы найти сумму этих векторов, нужно просто сложить соответствующие координаты каждого вектора и получить новые координаты для вектора суммы. Таким образом, новый вектор D с координатами (Dx, Dy, Dz) будет являться суммой векторов A, B и C.
Что такое вектор?

Векторы используются во многих областях, таких как физика, геометрия, компьютерная графика и т.д. Они позволяют описывать и моделировать различные физические величины, такие как скорость, сила или смещение. Векторы могут быть складываться, вычитаться, умножаться на число и подвергаться другим математическим операциям, что позволяет более точно описывать и анализировать различные явления и процессы.
Важно отметить, что вектор не является просто набором чисел, а математическим объектом с определенными свойствами и операциями. Он играет важную роль в анализе и моделировании различных явлений и процессов, поэтому понимание его сущности и применения очень полезно.
Сложение векторов: базовые понятия

Векторы могут быть представлены как направленные отрезки на плоскости или в пространстве. Они имеют длину, направление и начальную точку. Для сложения векторов необходимо совместить их начальные точки, а затем провести новый вектор от начальной точки первого вектора к конечной точке последнего вектора.
Векторы складываются поэлементно: сумма соответствующих координат векторов даёт координаты суммы. Например, для двух трехмерных векторов (a₁, a₂, a₃) и (b₁, b₂, b₃) их сумма будет иметь координаты (a₁ + b₁, a₂ + b₂, a₃ + b₃). Аналогичные правила применяются и для сложения трёх и более векторов.
Важно: при сложении векторов необходимо учитывать их направление и ориентацию в пространстве. Сумма векторов будет иметь другое значение, если векторы имеют противоположную ориентацию или расположены в разных квадрантах.
Сложение векторов широко применяется в физике, геометрии, компьютерной графике и других областях. Понимание основных понятий и правил сложения векторов является необходимым для успешного решения задач и изучения дальнейших тем в векторной алгебре.
Координатная система
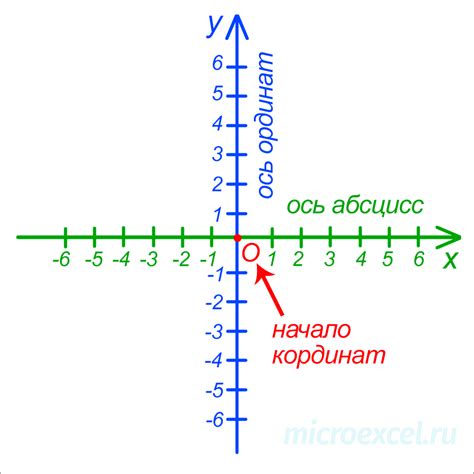
В двумерной координатной системе каждая точка задается двумя числами - координатами (x, y), где x - это горизонтальная ось, а y - вертикальная ось. Ориентиры x и y называются осями координат.
Чтобы найти сумму трех векторов по координатам, необходимо сложить соответствующие координаты каждого вектора. Например, сумма трех векторов (x₁, y₁), (x₂, y₂) и (x₃, y₃) будет равна (x₁ + x₂ + x₃, y₁ + y₂ + y₃).
Координатная система также может быть расширена до трех измерений, добавляя дополнительную ось z. В трехмерной координатной системе каждая точка задается тремя числами - координатами (x, y, z).
Координатная система имеет множество применений, например, для построения графиков функций, описания местоположений в пространстве, определения направления движения объектов и многое другое.
Сложение векторов по координатам
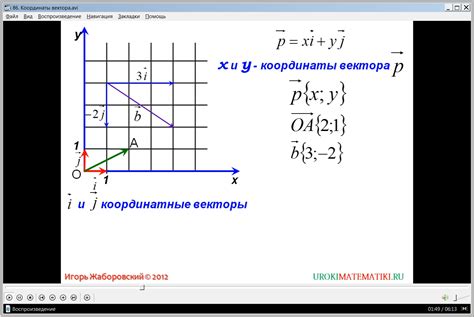
Для сложения векторов по координатам необходимо сложить соответствующие компоненты векторов. Если у нас есть три вектора A, B и C, заданные следующим образом:
A = (x1, y1, z1)
B = (x2, y2, z2)
C = (x3, y3, z3)
Тогда их сумма D будет равна
D = A + B + C = (x1 + x2 + x3, y1 + y2 + y3, z1 + z2 + z3)
Таким образом, для сложения векторов по координатам необходимо сложить соответствующие координаты векторов.
Сложение векторов по координатам является основой многих операций в линейной алгебре, таких как вычитание векторов, умножение на скаляр и нахождение среднего значения векторов. Понимание этого метода сложения векторов по координатам является важным для работы со множеством векторов.
Шаги для нахождения суммы трех векторов
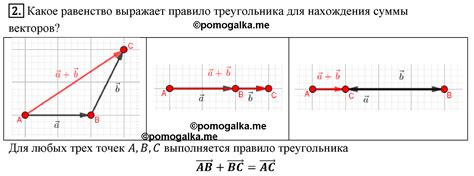
Для нахождения суммы трех векторов по их координатам необходимо выполнить следующие шаги:
- Задать координаты каждого вектора. Назовем их векторами A, B и C. Например, A = (a₁, a₂, a₃), B = (b₁, b₂, b₃) и C = (c₁, c₂, c₃).
- Сложить соответствующие координаты каждого вектора. Например, сложить a₁ с b₁ и c₁, получив сумму по оси x.
- Повторить предыдущий шаг для всех остальных осей (y и z), получив суммы по каждой оси.
- Сформировать новый вектор D = (d₁, d₂, d₃), где d₁ - сумма по оси x, d₂ - сумма по оси y, и d₃ - сумма по оси z.
Полученный вектор D будет являться суммой векторов A, B и C по их координатам.