Углы треугольника – основные понятия, которые обязательно изучают ученики в 7 классе геометрии. Они являются основой для решения различных задач и построений. Каждый треугольник состоит из трех углов, как бы сложно он ни выглядел. Важно помнить, что сумма всех углов треугольника всегда равна некоторой постоянной величине.

Согласно правилу геометрии, сумма всех углов в треугольнике равна 180 градусам. Данное правило работает для любого треугольника, независимо от его размеров и формы. Ведь суть углов заключается в их отношении друг к другу, а не в самом треугольнике.

Например, если у нас есть треугольник с углами размерами 45, 60 и 75 градусов, то сумма этих углов будет равна 45 + 60 + 75 = 180 градусов. Это подтверждает правило, о котором говорилось ранее.

Понимание, что сумма углов треугольника всегда равна 180 градусам, поможет ученикам быстро и легко решать различные задачи, связанные с треугольниками. Например, можно найти один из углов по известным углам, либо найти площадь треугольника, зная два угла и гипотенузу. Важно уметь применять это правило на практике для успешного изучения геометрии.

Формула для расчета суммы углов треугольника

Сумма углов треугольника равна 180 градусам.

Это фундаментальное правило геометрии, которое можно использовать для расчета углов треугольника.

Каждый треугольник состоит из трех углов, которые являются внутренними углами треугольника.

Суммируя все внутренние углы треугольника, получим их полную сумму, которая всегда будет равна 180 градусам.

Это свойство треугольников основывается на постулате о внешнем угле треугольника, который всегда равен сумме двух внутренних углов.

Таким образом, зная значения двух углов треугольника, всегда можно вычислить значение третьего угла с помощью формулы:

Значение третьего угла = 180 - (значение первого угла + значение второго угла)

Например, если первый угол треугольника равен 40 градусам, а второй угол равен 60 градусам:

Значение третьего угла = 180 - (40 + 60) = 80 градусов.

Эта формула является основной для расчета углов треугольников и помогает определить недостающее значение угла по известным углам.

Используя эту формулу, можно решать задачи по геометрии, связанные с треугольниками, и определять значения углов с высокой точностью.

Знание этой формулы позволяет не только понять свойства треугольников, но и применять их в различных практических ситуациях.

Оно полезно не только для учебы, но и для повседневной жизни, например, при строительстве и дизайне.

Как найти сумму углов треугольника

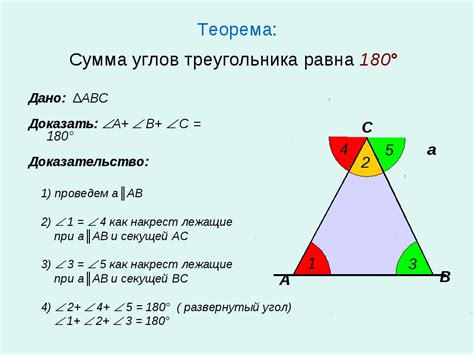
Сумма углов треугольника всегда равна 180 градусам. Это основное правило в геометрии, которое легко запомнить.

Для того чтобы найти сумму углов треугольника, достаточно сложить все углы, измеренные в градусах, и проверить, что полученная сумма равна 180 градусам.

Например, у нас есть треугольник, углы которого измеряются 60, 40 и 80 градусов. Чтобы найти сумму углов, мы складываем эти значения: 60 + 40 + 80 = 180 градусов. Полученная сумма равна 180 градусам, что подтверждает правильность расчета.

Если сумма углов треугольника не равна 180 градусам, значит была допущена ошибка в измерении или расчете углов.

Знание правила суммы углов треугольника позволяет не только проверять правильность результатов, но и использовать его для решения геометрических задач. Например, если мы знаем значения двух углов треугольника, можем легко найти значение третьего угла, вычитая из 180 градусов сумму уже известных углов.

Теперь вы знаете, как найти сумму углов треугольника и использовать это знание для решения геометрических задач.

Примеры расчета суммы углов треугольника

Сумма углов внутри треугольника всегда равна 180 градусам. Ниже представлены примеры расчета суммы углов треугольника:

Пример 1:

Пусть дан треугольник ABC. Угол A равен 60 градусам, угол B равен 50 градусам. Найдем угол C.

Известно, что сумма углов треугольника равна 180 градусам. Значит, угол C = 180 - 60 - 50 = 70 градусам.

Пример 2:

Пусть дан треугольник XYZ. Угол X равен 90 градусам, угол Y равен 45 градусам. Найдем угол Z.

Сумма угла X и угла Y равна 90 + 45 = 135 градусам. Значит, угол Z = 180 - 135 = 45 градусам.

Пример 3:

Пусть дан треугольник PQR. Угол P равен 30 градусам, угол R равен 50 градусам. Найдем угол Q.

Сумма угла P и угла R равна 30 + 50 = 80 градусам. Значит, угол Q = 180 - 80 = 100 градусам.

Эти примеры показывают, как можно находить неизвестные углы в треугольнике, зная сумму углов 180 градусов и известные углы. Это правило помогает решать задачи по геометрии, связанные с треугольниками.