Как вычислить тангенс по синусу и углу — формулы и примеры

На чтение 6 мин Опубликовано 14.11.2024 Обновлено 14.11.2024

Тангенс – это геометрическая характеристика треугольника, которая определяет соотношение между его противоположной и прилежащей сторонами. Изучение тангенса является одной из важных тем в математике и физике, так как он широко применяется для решения задач в этих науках.

Если вам известны синус и угол треугольника, вы можете легко вычислить его тангенс, используя специальные формулы. Формула для вычисления тангенса по синусу и углу:

тангенс угла = синус угла / косинус угла

Таким образом, для вычисления тангенса достаточно разделить значение синуса угла на его косинус.

Рассмотрим пример. Пусть у нас есть треугольник, угол которого равен 30 градусам, а значение синуса этого угла равно 0,5. Чтобы вычислить тангенс этого угла, мы должны разделить значение синуса на косинус. Значение косинуса угла 30 градусов равно √3 / 2, поэтому:

тангенс 30 градусов = 0,5 / (√3 / 2) = 2 / √3 ≈ 1,155

Таким образом, тангенс угла 30 градусов приблизительно равен 1,155.

Теперь вы знаете, как вычислить тангенс по синусу и углу, используя простую формулу. Эта информация может быть полезна при решении различных задач, связанных с геометрией и науками о природе.

Как получить тангенс?

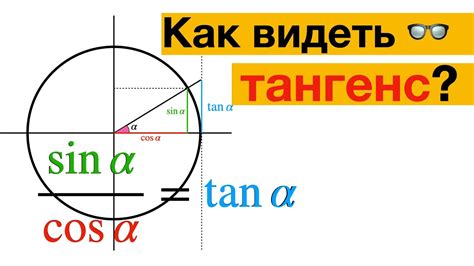
Тангенс угла можно вычислить, зная значение синуса и косинуса данного угла. Формула для вычисления тангенса угла α:

tg(α) = sin(α) / cos(α)

Для получения значения тангенса необходимо разделить синус угла на косинус угла.

Пример:

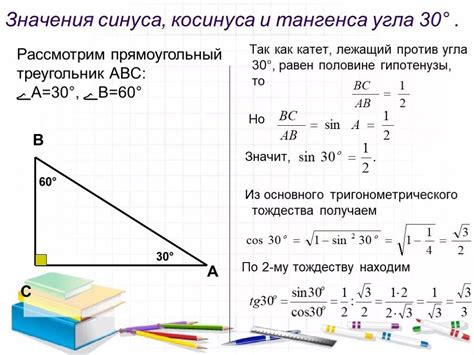
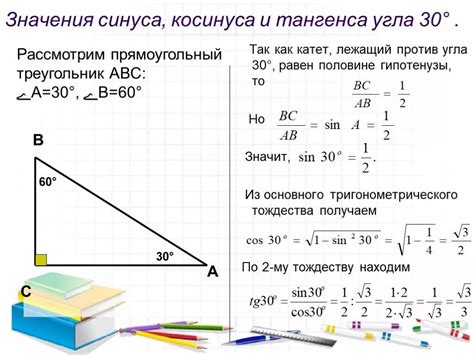
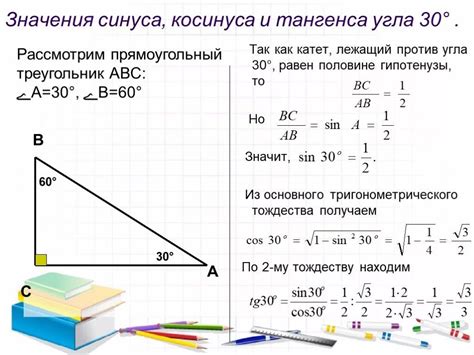
Допустим, у нас есть треугольник ABC, в котором угол B равен 30° и известен синус этого угла: sin(30°) = 0.5. Чтобы найти тангенс угла B, нужно:

1. Найти косинус угла B. Так как сумма углов в треугольнике равна 180°, то угол A равен 60°. Таким образом, sin(60°) = √3 / 2. Используя формулу Pythagorean identity, находим cos(30°) = √3 / 2.

2. Подставить значения sin(30°) и cos(30°) в формулу для тангенса: tg(30°) = sin(30°) / cos(30°) = 0.5 / (√3 / 2) = √3 / 3 ≈ 0.577.

Таким образом, тангенс угла B равен примерно 0.577.

Формула вычисления тангенса

Формула для вычисления тангенса угла α:

Тангенс α = sin α / cos α
Тангенс α = sin α ÷ cos α

Для вычисления тангенса угла α необходимо знать значения синуса и косинуса угла. Синус угла α равен отношению противоположной стороны к гипотенузе треугольника, а косинус угла α – отношению прилежащей стороны к гипотенузе.

Пример вычисления тангенса:

Пусть задан угол α = 30 градусов.
Вычислим синус угла α: sin α = 1/2
Вычислим косинус угла α: cos α = √3/2
Подставим значения синуса и косинуса в формулу: тангенс α = (1/2) / (√3/2) = 1/√3 = √3/3

Таким образом, тангенс угла α при α = 30 градусов равен √3/3.

Пример вычисления тангенса

Предположим, у нас есть треугольник с известными значениями синуса и угла. Используя эти значения, мы можем вычислить тангенс угла.

Допустим, у нас есть треугольник со значением синуса равным 0,6 и углом равным 45 градусов. Мы хотим найти значение тангенса этого угла.

Для вычисления тангенса угла мы можем использовать формулу:

тангенс = синус / косинус

В данном случае, у нас уже есть значение синуса (0,6), поэтому нам необходимо найти значение косинуса.

Мы можем использовать формулу:

косинус = √(1 - синус²)

Подставляя значение синуса в эту формулу, мы получим:

косинус = √(1 - 0,6²)

косинус = √(1 - 0,36)

косинус = √0,64

косинус ≈ 0,8

Теперь мы знаем значения синуса (0,6) и косинуса (0,8), и можем вычислить тангенс, подставив их в формулу:

тангенс = синус / косинус

тангенс = 0,6 / 0,8

тангенс ≈ 0,75

Таким образом, тангенс угла 45 градусов с синусом 0,6 примерно равен 0,75.

Как вычислить тангенс по синусу?

Для вычисления тангенса по синусу и углу можно воспользоваться следующей формулой:

тангенс угла = синус угла / косинус угла

Для вычисления значений тангенса можно использовать как тригонометрические таблицы, так и калькуляторы с функцией вычисления тригонометрических функций.

Например, если известно значение синуса угла и косинуса угла, можно воспользоваться формулой для вычисления тангенса:

Пример:

Допустим, известно, что синус угла равен 0.6, а косинус угла равен 0.8. Для вычисления тангенса по синусу и углу подставим значения в формулу:

тангенс угла = 0.6 / 0.8 = 0.75

Таким образом, тангенс угла будет равен 0.75.

Формула вычисления тангенса по синусу

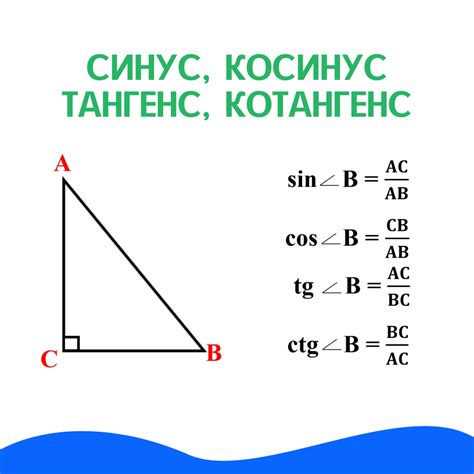
Тангенс угла можно вычислить, зная его синус, по следующей формуле:

тангенс угла = синус угла / корень из (1 - синус^2 угла)

Эта формула основана на определении тангенса как отношения синуса к косинусу угла.

Применив эту формулу, можно легко вычислить значение тангенса угла по известному значению его синуса. Например, если синус угла равен 0.6, то:

тангенс угла = 0.6 / корень из (1 - 0.6^2) ≈ 0.8

Таким образом, тангенс угла будет примерно равен 0.8.

Пример вычисления тангенса по синусу

Для вычисления тангенса по синусу и углу, мы можем воспользоваться формулой:

тангенс = синус / косинус

Давайте представим, что у нас есть треугольник с углом α и гипотенузой, длина которой равна 1. Мы также знаем, что синус угла α равен 0.8.

Чтобы вычислить косинус угла α, мы можем воспользоваться формулой:

косинус = √(1 - синус^2)

В данном случае, мы можем вычислить:

косинус = √(1 - 0.8^2) = √(1 - 0.64) = √(0.36) ≈ 0.6

Теперь, зная значение синуса и косинуса, мы можем использовать формулу для вычисления тангенса:

тангенс = 0.8 / 0.6 ≈ 1.333

Таким образом, тангенс угла α равен примерно 1.333.

Как вычислить тангенс по углу?

Формула для вычисления тангенса угла:

tan(𝜃) = sin(𝜃)/cos(𝜃)

где 𝜃 - заданный угол.

Пример:

Пусть 𝜃 = 45°. Чтобы вычислить тангенс данного угла, нужно сначала вычислить синус и косинус угла, а затем поделить синус на косинус:

sin(𝜃) = sin(45°) ≈ 0.7071

cos(𝜃) = cos(45°) ≈ 0.7071

tan(𝜃) = sin(𝜃)/cos(𝜃) = 0.7071/0.7071 = 1

Таким образом, тангенс угла 45° равен 1.

Формула вычисления тангенса по углу

Для вычисления тангенса по углу используется следующая формула:

tan(α) = sin(α) / cos(α)

Где:

α – измеряемый угол, измеряемый в радианах или градусах;
sin(α) – значение синуса угла α;
cos(α) – значение косинуса угла α.

Для вычисления тангенса по углу необходимо знать значения синуса и косинуса этого угла. Синус и косинус угла можно определить с помощью trigonometric функций в языках программирования или использовать таблицы значений синуса и косинуса.

Пример вычисления тангенса по углу:

Задан угол α = 45 градусов.
Найдем синус угла α: sin(45°) = 0.7071.
Найдем косинус угла α: cos(45°) = 0.7071.
Рассчитаем тангенс угла α: tan(45°) = sin(45°) / cos(45°) = 0.7071 / 0.7071 = 1.

Таким образом, тангенс угла α равен 1 для данного примера.

Пример вычисления тангенса по углу

Допустим, нужно вычислить тангенс угла α, у которого синус равен 0,8.

Воспользуемся формулой:

tg(α) = sin(α) / cos(α)

Так как нам уже известен синус угла α (0,8), нам остаётся найти значение косинуса для этого угла.

Зная, что синус угла α равен 0,8, можно воспользоваться тригонометрической формулой:

sin²(α) + cos²(α) = 1

В нашем случае:

0,8² + cos²(α) = 1

0,64 + cos²(α) = 1

cos²(α) = 1 - 0,64

cos²(α) = 0,36

cos(α) = √(0,36)

cos(α) = 0,6

Теперь, имея значения синуса и косинуса, мы можем вычислить тангенс угла α:

tg(α) = sin(α) / cos(α) = 0,8 / 0,6 = 1,33

Таким образом, тангенс угла α равен 1,33.

Как вычислить тангенс по синусу и углу — формулы и примеры

На чтение 6 мин Опубликовано 14.11.2024 Обновлено 14.11.2024

тангенс угла = синус угла / косинус угла

Таким образом, для вычисления тангенса достаточно разделить значение синуса угла на его косинус.

тангенс 30 градусов = 0,5 / (√3 / 2) = 2 / √3 ≈ 1,155

Таким образом, тангенс угла 30 градусов приблизительно равен 1,155.

Как получить тангенс?

tg(α) = sin(α) / cos(α)

Для получения значения тангенса необходимо разделить синус угла на косинус угла.

Пример:

2. Подставить значения sin(30°) и cos(30°) в формулу для тангенса: tg(30°) = sin(30°) / cos(30°) = 0.5 / (√3 / 2) = √3 / 3 ≈ 0.577.

Таким образом, тангенс угла B равен примерно 0.577.

Формула вычисления тангенса

Формула для вычисления тангенса угла α:

Тангенс α = sin α / cos α
Тангенс α = sin α ÷ cos α

Пример вычисления тангенса:

Пусть задан угол α = 30 градусов.
Вычислим синус угла α: sin α = 1/2
Вычислим косинус угла α: cos α = √3/2
Подставим значения синуса и косинуса в формулу: тангенс α = (1/2) / (√3/2) = 1/√3 = √3/3

Таким образом, тангенс угла α при α = 30 градусов равен √3/3.

Пример вычисления тангенса

Для вычисления тангенса угла мы можем использовать формулу:

тангенс = синус / косинус

В данном случае, у нас уже есть значение синуса (0,6), поэтому нам необходимо найти значение косинуса.

Мы можем использовать формулу:

косинус = √(1 - синус²)

Подставляя значение синуса в эту формулу, мы получим:

косинус = √(1 - 0,6²)

косинус = √(1 - 0,36)

косинус = √0,64

косинус ≈ 0,8

Теперь мы знаем значения синуса (0,6) и косинуса (0,8), и можем вычислить тангенс, подставив их в формулу:

тангенс = синус / косинус

тангенс = 0,6 / 0,8

тангенс ≈ 0,75

Таким образом, тангенс угла 45 градусов с синусом 0,6 примерно равен 0,75.

Как вычислить тангенс по синусу?

Для вычисления тангенса по синусу и углу можно воспользоваться следующей формулой:

тангенс угла = синус угла / косинус угла

Пример:

тангенс угла = 0.6 / 0.8 = 0.75

Таким образом, тангенс угла будет равен 0.75.

Формула вычисления тангенса по синусу

Тангенс угла можно вычислить, зная его синус, по следующей формуле:

тангенс угла = синус угла / корень из (1 - синус^2 угла)

Эта формула основана на определении тангенса как отношения синуса к косинусу угла.

тангенс угла = 0.6 / корень из (1 - 0.6^2) ≈ 0.8

Таким образом, тангенс угла будет примерно равен 0.8.

Пример вычисления тангенса по синусу

Для вычисления тангенса по синусу и углу, мы можем воспользоваться формулой:

тангенс = синус / косинус

Чтобы вычислить косинус угла α, мы можем воспользоваться формулой:

косинус = √(1 - синус^2)

В данном случае, мы можем вычислить:

косинус = √(1 - 0.8^2) = √(1 - 0.64) = √(0.36) ≈ 0.6

Теперь, зная значение синуса и косинуса, мы можем использовать формулу для вычисления тангенса:

тангенс = 0.8 / 0.6 ≈ 1.333

Таким образом, тангенс угла α равен примерно 1.333.

Как вычислить тангенс по углу?

Формула для вычисления тангенса угла:

tan(𝜃) = sin(𝜃)/cos(𝜃)

где 𝜃 - заданный угол.

Пример:

sin(𝜃) = sin(45°) ≈ 0.7071

cos(𝜃) = cos(45°) ≈ 0.7071

tan(𝜃) = sin(𝜃)/cos(𝜃) = 0.7071/0.7071 = 1

Таким образом, тангенс угла 45° равен 1.

Формула вычисления тангенса по углу

Для вычисления тангенса по углу используется следующая формула:

tan(α) = sin(α) / cos(α)

Где:

α – измеряемый угол, измеряемый в радианах или градусах;
sin(α) – значение синуса угла α;
cos(α) – значение косинуса угла α.

Пример вычисления тангенса по углу:

Задан угол α = 45 градусов.
Найдем синус угла α: sin(45°) = 0.7071.
Найдем косинус угла α: cos(45°) = 0.7071.
Рассчитаем тангенс угла α: tan(45°) = sin(45°) / cos(45°) = 0.7071 / 0.7071 = 1.

Таким образом, тангенс угла α равен 1 для данного примера.

Пример вычисления тангенса по углу

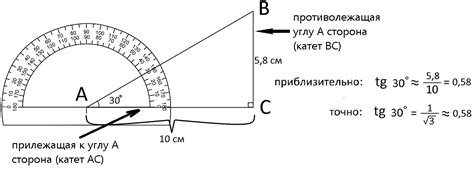
Допустим, нужно вычислить тангенс угла α, у которого синус равен 0,8.

Воспользуемся формулой:

tg(α) = sin(α) / cos(α)

Так как нам уже известен синус угла α (0,8), нам остаётся найти значение косинуса для этого угла.

Зная, что синус угла α равен 0,8, можно воспользоваться тригонометрической формулой:

sin²(α) + cos²(α) = 1

В нашем случае:

0,8² + cos²(α) = 1

0,64 + cos²(α) = 1

cos²(α) = 1 - 0,64

cos²(α) = 0,36

cos(α) = √(0,36)

cos(α) = 0,6

Теперь, имея значения синуса и косинуса, мы можем вычислить тангенс угла α:

tg(α) = sin(α) / cos(α) = 0,8 / 0,6 = 1,33

Таким образом, тангенс угла α равен 1,33.