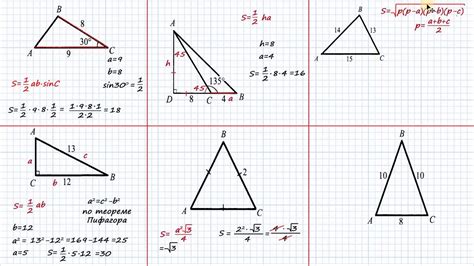
Тангенс треугольника – это одна из основных тригонометрических функций, которая помогает нам определить соотношение между сторонами треугольника и углом, противолежащим этой стороне. Если у вас есть задача, связанная с нахождением тангенса треугольника по клеточкам ОГЭ, то у вас появляется возможность применить свои знания по теореме Пифагора и выразить тангенс через синус и косинус угла.

Чтобы решить подобную задачу, следует учесть следующие шаги:

1. Определите изначально данные треугольника, такие как стороны или углы.

2. Разберите треугольник на отдельные составляющие, исходя из вершин, углов или сторон, составляющих треугольник.

3. Примените теорему Пифагора для определения отношения сторон и оценки значений синуса или косинуса искомого угла.

4. Используя полученные значения синуса или косинуса, вычислите тангенс угла треугольника.

Важно помнить, что для решения такой задачи необходимы базовые знания тригонометрии, особенно формулы тригонометрических функций и теоремы Пифагора. Эти знания позволят вам правильно решить задачу и получить искомое значение тангенса треугольника по клеточкам ОГЭ.

Описание процесса нахождения тангенса треугольника по клеточкам ОГЭ

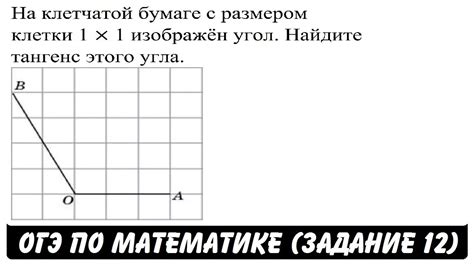
Для нахождения тангенса треугольника по клеточкам ОГЭ необходимо выполнить следующие шаги:

1. Найти значения сторон треугольника, используя информацию, представленную в клеточках задания. Обычно в задании указываются значения двух сторон треугольника и одного угла.
2. Используя найденные значения сторон, найти значения всех углов треугольника с помощью теоремы косинусов или других геометрических формул.
3. Найденные значения углов треугольника позволяют найти значения соответствующих тригонометрических функций. В данном случае нас интересует тангенс угла треугольника.
4. Для нахождения тангенса угла треугольника необходимо взять отношение противолежащей стороны к прилежащей стороне по формуле: тангенс угла = противолежащая сторона / прилежащая сторона.

После выполнения этих шагов можно получить значение тангенса треугольника по клеточкам ОГЭ. Важно помнить, что для точного результата необходимо проводить все вычисления внимательно и быть внимательным при считывании значений из клеточек задания.

Выявление основных понятий

Перед тем, как начать решение задачи на нахождение тангенса треугольника по клеточкам, необходимо разобраться в некоторых важных понятиях.

Треугольник – это геометрическая фигура, состоящая из трех отрезков, называемых сторонами треугольника. Стороны треугольника соединяются в трех точках, называемых вершинами треугольника.

Угол – это область плоскости, ограниченная двумя лучами с общим началом, называемым вершиной угла. Вершина угла указывает на точку пересечения двух лучей, а стороны угла – на отрезки, которые ограничивают этот угол.

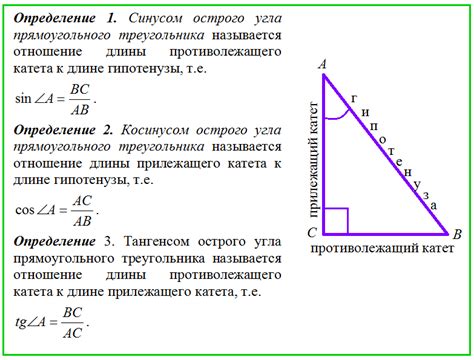
Гипотенуза – это наибольшая сторона прямоугольного треугольника, которая является противоположной прямому углу.

Катет – это одна из двух меньших сторон прямоугольного треугольника, которые прилегают к прямому углу.

Тангенс – это тригонометрическая функция, которая равна отношению длины противоположного катета к длине прилежащего катета в прямоугольном треугольнике.

Теперь, когда мы познакомились с основными понятиями, можно перейти к решению задачи на нахождение тангенса треугольника по клеточкам.

Правила нахождения тангенса

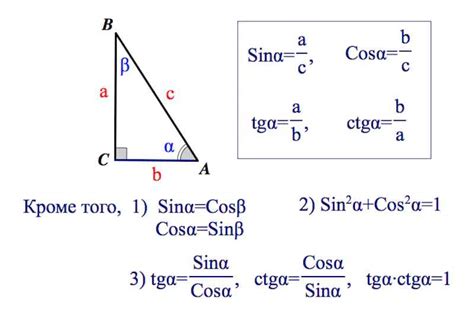
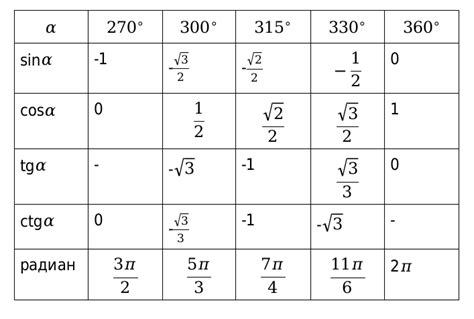
Тангенс треугольника можно найти, зная значения длин его сторон или отношение длин сторон.

Правило 1: Если известны значения длин сторон треугольника, то тангенс можно найти с помощью следующей формулы:

тангенс угла = противоположная сторона / прилежащая сторона

Правило 2: Если известно отношение длин сторон треугольника, то можно использовать следующую формулу:

тангенс угла = значение отношения (размер коэффициента)

Например, если отношение длин сторон треугольника составляет 3:4, то тангенс угла будет равен 3/4.

Зная значения тангенса угла, можно решать различные задачи и находить неизвестные значения сторон и углов треугольника.

Графическое представление треугольника

Графическое представление треугольника позволяет визуализировать его структуру и основные элементы. На графике треугольника обычно изображены его вершины, стороны и углы, что помогает уяснить его геометрические свойства.

Вершины треугольника обозначаются буквами A, B и C. Стороны треугольника обычно обозначаются соответствующими буквами в нижнем индексе, например, AB, BC и CA. Углы треугольника обозначаются буквами в верхнем индексе, например, ∠A, ∠B и ∠C.

Графическое представление треугольника также включает рисование сторон и углов. Стороны треугольника изображаются с помощью отрезков, а углы – с помощью замкнутых дуг, указывающих направление поворота.

Графическое представление треугольника может использоваться для решения задач, связанных с нахождением различных величин, например, тангенса угла треугольника. Кроме того, оно помогает визуализировать геометрические свойства треугольника и легче понять его структуру и связь между сторонами и углами.

Использование графического представления треугольника может значительно упростить решение задач и помочь в более полном понимании геометрических концепций.

Определение вершин треугольника по клеточкам

Для определения вершин треугольника по клеточкам необходимо использовать координатную систему, где каждая клеточка имеет свои координаты. Для простоты будем считать, что каждая клетка находится в одном из углов единичного квадрата, и ее координатами будут ее координаты на плоскости.

Допустим, у нас имеется треугольник, вершины которого лежат на клетках с координатами (x1, y1), (x2, y2) и (x3, y3). Чтобы определить эти координаты, достаточно взглянуть на их положение относительно других клеток. Используя свойства геометрических фигур, можно определить координаты вершин треугольника.

Например, если клетка (x1, y1) является вершиной треугольника, то все клетки, у которых x-координата меньше x1 и y-координата меньше y1, будут лежать внутри треугольника. Аналогично можно определить координаты остальных вершин треугольника.

Определение вершин треугольника по клеточкам может быть полезным, например, при решении задач по геометрии на Олимпиаде ГТО. Зная координаты вершин треугольника, можно вычислить его площадь, периметр и другие характеристики, а также провести много различных геометрических построений.

Расчет длин сторон треугольника

Для нахождения тангенса треугольника по клеточкам на плоскости ОГЭ, необходимо сначала рассчитать длины его сторон.

Для этого можно воспользоваться формулой расстояния между двумя точками в декартовой системе координат:

• Для вычисления длины горизонтальной стороны треугольника можно использовать формулу: \(d = |x_2 - x_1|\), где \(x_1\) и \(x_2\) - горизонтальные координаты соответствующих точек.
• Аналогично, для вычисления длины вертикальной стороны треугольника используется формула: \(d = |y_2 - y_1|\), где \(y_1\) и \(y_2\) - вертикальные координаты соответствующих точек.

После расчета длин сторон треугольника можно перейти к нахождению его тангенса по формуле:

\(tg(\alpha) = \frac{{\text{вертикальная сторона}}}{{\text{горизонтальная сторона}}}\)

Таким образом, зная длины сторон треугольника, можно легко рассчитать его тангенс и узнать ответ на задачу.

Вычисление значения тангенса по формуле

Для вычисления значения тангенса треугольника по клеточкам можно использовать следующую формулу:

• Найдите значение побочного катета, соответствующего клеточкам на стороне, противоположной углу, для которого требуется вычислить тангенс. Это можно сделать, вычитая номер клетки нижнего угла треугольника из номера клетки верхнего угла этой стороны. Обозначим это значение как "a".
• Найдите значение основания треугольника, соответствующего клеточкам на стороне, прилегающей к углу, для которого требуется вычислить тангенс. Это можно сделать, вычитая номер клетки нижнего угла этой стороны из номера клетки верхнего угла этой стороны. Обозначим это значение как "b".
• Вычислите значение тангенса по формуле: 𝑡𝑔(𝜃)= 𝑎/𝑏, где 𝑡𝑔 - тангенс, 𝜃 - угол, 𝑎 - значение побочного катета, 𝑏 - значение основания треугольника.

Таким образом, заданные значения клеточек можно использовать для вычисления требуемого значения тангенса треугольника.

Пример вычисления тангенса треугольника по клеточкам ОГЭ

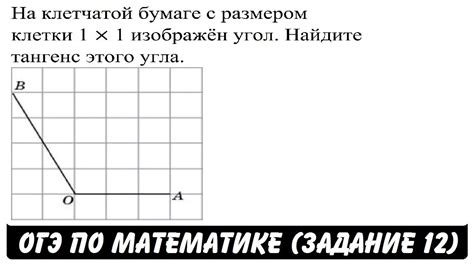
Для вычисления тангенса треугольника по клеточкам на задание ОГЭ, нужно :

1. Определить стороны треугольника. Для этого найдите разницу между значениями координат на горизонтали и вертикали. Например, если координаты верхней точки треугольника: A(x₁, y₁), координаты левой точки: B(x₂, y₂), то сторона AB будет равна (x₂ - x₁), а сторона BC будет равна (y₁ - y₂).
2. Вычислить противоположную и прилежащую стороны треугольника. Противоположной стороной считается сторона, соединяющая рассматриваемый угол с противоположной вершиной, а прилежащей стороной - сторона, соединяющая рассматриваемый угол с вершиной, с которой он образует эту сторону. Например, в треугольнике ABC с прямым углом в вершине B, сторона AB является противоположной стороной, а сторона BC - прилежащей стороной, при вычислении тангенса угла A.
3. Вычислить значение тангенса. Тангенс угла в треугольнике вычисляется как отношение противоположной стороны к прилежащей. Для вычисления тангенса угла A в треугольнике ABC, используйте формулу: tan(A) = противоположная сторона / прилежащая сторона.

Теперь у вас есть инструкция по вычислению тангенса треугольника по клеточкам на задание ОГЭ. Попробуйте применить это знание на практике и успешно решать задачи на ОГЭ!

Полезные советы и рекомендации

Для нахождения тангенса треугольника по клеточкам на ОГЭ следуйте следующим полезным советам и рекомендациям:

1. Тщательно читайте и анализируйте условие задачи, чтобы понять, что от вас требуется.
2. Обратите внимание на вид треугольника (прямоугольный, остроугольный или тупоугольный) и его стороны.
3. Измерьте длины сторон треугольника, используя масштаб на клетчатой бумаге, чтобы получить точные данные.
4. Используйте соответствующую формулу для вычисления тангенса треугольника в зависимости от известных данных.
5. Будьте внимательны при подсчете и умножении чисел, чтобы избежать ошибок.
6. Проверьте свой ответ, сравнив его с другими доступными данными или использовав геометрические свойства треугольника.
7. Практикуйтесь в решении подобных задач треугольников с использованием клеточек, чтобы стать более опытным в этой области.

Следуя этим советам и рекомендациям, вы сможете успешно находить значение тангенса треугольника по клеточкам на ОГЭ.