Тангенс угла - это одна из основных тригонометрических функций, которая показывает отношение противоположной и стороны к прилежащей стороне прямоугольного треугольника. Если вам известен синус угла, то существует несколько методов и формул, позволяющих вычислить тангенс этого угла.
Один из подходов к поиску тангенса угла с известным синусом - использование трех основных тригонометрических функций: синуса, косинуса и тангенса. Для этого можно воспользоваться такой формулой:
тангенс угла = синус угла / косинус угла
Воспользуемся примером для более наглядного объяснения. Предположим, что у нас есть треугольник, угол в котором имеет синус 0.6 (это может быть задача или конкретный случай). По формуле мы получим:
тангенс угла = 0.6 / косинус угла
Получив такое уравнение, мы можем решить его, найдя косинус угла используя другие соотношения тригонометрии или таблицы значений. После этого мы сможем точно определить тангенс искомого угла.
Методы и формулы для вычисления тангенса угла с помощью синуса

Есть несколько формул, которые позволяют найти тангенс угла, используя его синус.
Тангенс угла можно найти с помощью формулы:
| Формула | Описание |
|---|---|
| tg(α) = sin(α) / cos(α) | Данная формула выражает тангенс угла через синус и косинус угла. |
Для вычисления тангенса угла с помощью синуса можно использовать следующие методы:
1. Использование таблиц тригонометрических функций: существуют специальные таблицы, в которых записаны значения синуса, косинуса и тангенса для различных углов. Найдите в таблице значение синуса вашего угла и используйте соответствующее значение тангенса.
2. Использование калькулятора: многие калькуляторы имеют встроенные функции синуса и тангенса. Введите значение синуса угла и воспользуйтесь функцией, чтобы найти тангенс.
3. Использование математического софта: существует множество программ и онлайн-ресурсов, которые могут вычислить тангенс угла по заданному синусу. Введите значение синуса и воспользуйтесь соответствующей функцией, чтобы получить тангенс.
Все эти методы и формулы позволяют найти значение тангенса угла, зная его синус. Выберите подходящий для вас способ и примените его для решения ваших задач.
Тангенс угла с синусом: определение и связь со синусом
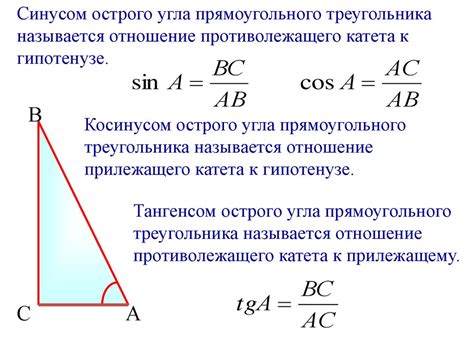
Также существует связь между тангенсом угла и его синусом. Она определяется формулой:
tg(α) = sin(α) / cos(α)
где α - угол в радианах.
Таким образом, для нахождения тангенса угла по известному значению синуса необходимо разделить значение синуса на значение косинуса данного угла.
Эта связь между тангенсом и синусом угла позволяет упростить расчеты и использовать их в различных задачах, связанных с геометрией, физикой и другими науками.
Формула для вычисления тангенса угла на основе значения синуса

Формула для вычисления тангенса угла на основе значения синуса имеет следующий вид:
tan(α) = sin(α) / √(1 - sin²(α))
В этой формуле α представляет собой значение угла, а sin(α) - значение синуса угла.
Эта формула основывается на математической связи между значением синуса и тангенса угла. Математически, тангенс угла определяется отношением синуса угла к косинусу угла. С помощью данной формулы можно выразить тангенс через синус, что может быть полезно в определенных вычислениях и задачах.
Зная значение синуса угла, можно использовать данную формулу для вычисления тангенса угла. Но необходимо учесть, что формула является приближенной и может иметь ограниченную точность в зависимости от значения угла и конкретных условий вычислений.
Таблица тангенсов углов с известным значением синуса
| Синус угла (sin) | Тангенс угла (tg) |
|---|---|
| 0 | 0 |
| 0.1 | 0.1003346729 |
| 0.2 | 0.2027100355 |
| 0.3 | 0.3093362496 |
| 0.4 | 0.4227932187 |
| 0.5 | 0.5463024898 |
| 0.6 | 0.6841368083 |
| 0.7 | 0.8390996312 |
| 0.8 | 1.0296385575 |
| 0.9 | 1.2601582176 |
Используя данную таблицу, можно вычислить тангенс угла, зная его значение синуса. Просто найдите нужное значение синуса в таблице и оно будет соответствовать значению тангенса угла.
Практические примеры вычисления тангенса угла с помощью синуса

Пример 1:
Допустим, у вас есть треугольник со сторонами a = 5 см и b = 12 см, а также известно, что угол между этими сторонами равен 30 градусов. Чтобы найти тангенс этого угла, можно воспользоваться формулой:
tg(θ) = sin(θ) / cos(θ)
Для нашего примера:
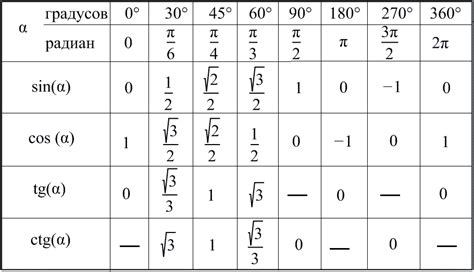
tg(30°) = sin(30°) / cos(30°)
sin(30°) = 0.5 (из таблицы значений), а cos(30°) = √(3)/2 (также из таблицы значений). Подставляя эти значения в формулу, получаем:
tg(30°) = 0.5 / (√(3)/2) = √(3)/3 ≈ 0.577
Пример 2:
Предположим, вы знаете, что sin(θ) = 0.8. Чтобы найти соответствующий тангенс угла, можно использовать формулу:
tg(θ) = sin(θ) / cos(θ)
Мы знаем только sin(θ), но не знаем cos(θ). Однако, с помощью тригонометрической формулы sin²(θ) + cos²(θ) = 1, можно найти отсутствующую величину:
sin²(θ) + cos²(θ) = 1
0.8² + cos²(θ) = 1
cos²(θ) = 1 - 0.64 = 0.36
cos(θ) = √(0.36) = 0.6
Теперь, подставляя значения sin(θ) = 0.8 и cos(θ) = 0.6 в формулу, можно вычислить тангенс:
tg(θ) = sin(θ) / cos(θ) = 0.8 / 0.6 = 1.33
Это лишь два примера использования синуса для вычисления тангенса угла. Такой подход может быть применен в различных задачах, связанных с геометрией, физикой, инженерией и других областях. Важно помнить, что в некоторых случаях может потребоваться применить обратные функции (арксинус, арккосинус) для получения угловых значений.