Тангенс - одна из основных тригонометрических функций, которая широко используется в математике, физике и других науках. Он позволяет нам определить отношение сторон прямоугольного треугольника и найти значение угла, если известны длины противоположенной и прилежащей сторон. В этой статье мы рассмотрим как найти тангенс угла в треугольнике и предоставим несколько примеров вычислений.
Для начала давайте вспомним определение тангенса. Тангенс угла в треугольнике определяется как отношение противоположенной стороны (стороны, не прилегающей к углу) к прилежащей стороне (стороне, прилегающей к углу).
Таким образом, формула для вычисления тангенса угла в треугольнике выглядит следующим образом: тангенс угла = противоположная сторона / прилежащая сторона.
Давайте рассмотрим пример. Предположим, у нас есть прямоугольный треугольник, у которого длина прилежащей стороны равна 4 и длина противоположенной стороны равна 3. Чтобы найти тангенс угла в этом треугольнике, мы должны разделить длину противоположенной стороны на длину прилежащей стороны: тангенс угла = 3 / 4 = 0.75.
Руководство по нахождению тангенса угла в треугольнике
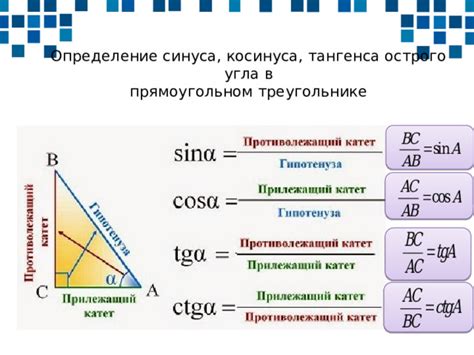
Для нахождения тангенса угла в треугольнике необходимо знать длины противолежащего и прилегающего катетов. Давайте рассмотрим пример:
| Стороны треугольника | Углы треугольника |
|---|---|
| Сторона a: 4 ед. | Угол A: 30° |
| Сторона b: 6 ед. | Угол B: 60° |
| Сторона c: 5 ед. | Угол C: 90° |
Чтобы найти тангенс угла A, мы должны разделить длину противолежащего катета a на длину прилегающего катета b. В данном примере:
Тангенс угла A = a / b = 4 / 6 = 0.6667
То есть, тангенс угла A равен 0.6667.
Аналогично, для нахождения тангенса угла B, мы делим длину противолежащего катета b на длину прилегающего катета a:
Тангенс угла B = b / a = 6 / 4 = 1.5
Значит, тангенс угла B равен 1.5.
Важно отметить, что угол C является прямым углом (90°), поэтому его тангенс равен бесконечности или неопределенности.
Теперь вы знаете, как найти тангенс угла в треугольнике при известных длинах катетов. Это полезное знание, которое может пригодиться в различных областях, включая физику, инженерию и строительство.
Понятие тангенса угла и его применение в геометрии

Тангенс угла широко применяется в геометрии для вычисления неизвестных размеров треугольников. Он может быть использован для определения углов треугольника, когда известны длины его сторон. Также, тангенс угла может быть использован для вычисления высоты треугольника относительно одного из его углов.
Для вычисления тангенса угла, необходимо знать значения длин противоположного и прилежащего катетов. Для этого можно использовать таблицу тангенсов, в которой указаны значения тангенсов различных углов. Если в таблице нет нужного значения, тангенс можно вычислить как отношение противоположного катета к прилежащему.
| Угол (градусы) | Тангенс угла |
|---|---|
| 0 | 0 |
| 30 | 0.5774 |
| 45 | 1 |
| 60 | 1.7321 |
| 90 | ∞ |
Применение тангенса угла в геометрии может быть полезным для решения различных задач, таких как нахождение высоты треугольника или определение противоположного или прилежащего катета по известным углу и длине другого катета.
Примеры вычислений тангенса угла в треугольнике

Для вычисления тангенса угла в треугольнике нужно знать значения противолежащей и прилежащей сторон. Вот несколько примеров вычисления тангенса угла:
| Пример | Противолежащая сторона (a) | Прилежащая сторона (b) | Тангенс угла (tan) |
|---|---|---|---|
| Пример 1 | 3 | 4 | 0.75 |
| Пример 2 | 5 | 12 | 0.4167 |
| Пример 3 | 8 | 15 | 0.5333 |
В каждом из этих примеров противолежащая сторона (a) и прилежащая сторона (b) заданы величинами. Для вычисления тангенса угла можно использовать формулу tan = a / b.
Таким образом, для первого примера, где a = 3 и b = 4, тангенс угла будет равен 0.75 (3 / 4 = 0.75).
При вычислении тангенса угла помните, что результат может быть представлен как десятичная дробь или дробь, в зависимости от точности требуемого ответа.