Углы являются одним из важных элементов геометрии. Они могут быть измерены в градусах, радианах или градах. Иногда возникает необходимость найти угол по известной дуге, и в этом случае есть простой метод, который может помочь.
Дуга - часть окружности, ограниченная двумя точками на окружности. Она измеряется в градусах и может быть меньше, равной или больше 180 градусов. Если известна дуга и радиус окружности, можно легко вычислить соответствующий угол.
Для того чтобы найти угол по известной дуге простым методом, необходимо знать формулу расчета. Формула выглядит следующим образом:
Угол = (Дуга / Длина окружности) * 360 градусов.
Эта формула основывается на том факте, что окружность составляет 360 градусов, а дуга представляет собой часть этой окружности.
С помощью этой простой формулы вы можете легко и быстро найти угол по известной дуге. Не забудьте знать длину окружности, чтобы точно рассчитать результат.
Определение угла и дуги
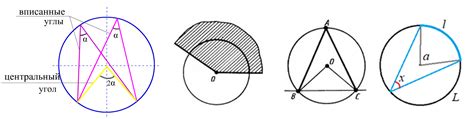
Угол – это геометрическая фигура, образованная двумя лучами с общим началом точки, называемой вершиной. Угол измеряется в градусах и обозначается символом °.
Дуга - это кривая линия, часть окружности, ограниченная двумя точками на окружности. Дуга измеряется в градусах и обозначается символом ° или в дробях относительно полного круга.
Чтобы найти угол по известной дуге с помощью простого метода, нужно воспользоваться формулой: угол равен дуге, разделенной на длину окружности и умноженной на 360, то есть:
Угол = (Дуга / Длина окружности) * 360
Простым примером является угол 90°, который соответствует четверть окружности. Если известна дуга, которая является четвертью окружности, можно легко определить угол с помощью формулы выше.
Таким образом, определение угла по известной дуге - это простой и математический метод, который позволяет найти соответствующий угол на основе известной части окружности.
Метод нахождения радиуса окружности
Если известны координаты центра окружности и одна точка на окружности, то радиус можно найти по формуле: r = √((x₁ - x)² + (y₁ - y)²), где (x₁, y₁) - координаты центра окружности, (x, y) - координаты точки на окружности.
Если известны длина дуги окружности и ее центральный угол (в радианах), то радиус можно найти по формуле: r = l/θ, где l - длина дуги, θ - центральный угол.
Для применения этой формулы, длина дуги должна быть задана в одних и тех же единицах измерения, что и радиус (например, в радианах или в градусах).
В некоторых случаях можно воспользоваться также готовыми таблицами значений, где для различных углов указаны соответствующие радиусы окружностей.
Иногда радиус окружности можно найти и графическим методом, используя изображение окружности и известную дугу.
Таким образом, методы нахождения радиуса окружности разнообразны и выбираются в зависимости от известных данных и условий задачи.
Вычисление длины дуги

Для вычисления длины дуги необходимо знать радиус окружности и угол, под которым она измеряется. Формула для вычисления длины дуги имеет вид:
L = r * α
где L - длина дуги, r - радиус окружности, α - угол в радианах.
Таким образом, чтобы вычислить длину дуги, необходимо умножить радиус окружности на значение угла, выраженное в радианах.
Для примера, предположим, что у нас есть окружность с радиусом 5 сантиметров, и мы хотим узнать, какая длина соответствует углу 30 градусов. Для этого необходимо перевести угол из градусов в радианы, используя соотношение:
α (рад) = α (град) * (π / 180)
В данном случае:
α (рад) = 30 * (π / 180) ≈ 0.5236 рад
Затем, мы можем использовать формулу для вычисления длины дуги:
L = 5 * 0.5236 ≈ 2.618 см
Таким образом, длина дуги при угле 30 градусов на окружности с радиусом 5 сантиметров составляет примерно 2.618 сантиметров.
Вычисление длины дуги позволяет нам получить информацию о криволинейном движении объекта на окружности и использовать эту информацию в различных задачах.
Определение центрального угла
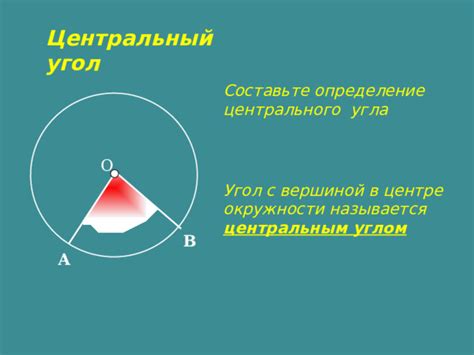
Для определения центрального угла по известной дуге простым методом необходимо:
- Измерить длину дуги (в сантиметрах).
- Используя формулу Угол = (Длина дуги / Длина окружности) * 360°, вычислить угол, где Длина окружности равна 2πr (где r – радиус окружности).
Найденный результат будет являться значением центрального угла в градусах.
Вот пример расчета центрального угла: если известна длина дуги и радиус окружности, можно использовать формулу:
| Длина дуги | Радиус окружности | Центральный угол |
|---|---|---|
| 15 см | 5 см | 108° |
Таким образом, для дуги длиной 15 см и радиуса окружности 5 см, центральный угол будет составлять 108°.
Расчет периферийного угла
Для расчета периферийного угла необходимо знать дугу и радиус, к которому были проведены радиусы. Формула для вычисления периферийного угла выглядит следующим образом:
Угол = (Длина дуги / Радиус) * 180 / π
Где:
Длина дуги – длина дуги, измеренная в выбранных единицах длины (например, в сантиметрах).
Радиус – радиус окружности, к которой были проведены радиусы, измеренный в тех же единицах длины, что и длина дуги.
π – математическая константа, примерное значение которой равно 3,14159 (или можно использовать более точное значение по таблицам или калькулятору).
Результат выражается в градусах.
Расчет периферийного угла по известной дуге – это простой метод, который позволяет быстро и точно определить величину угла между радиусами окружности.
Пример простого метода нахождения угла по известной дуге

Для нахождения угла по известной дуге можно воспользоваться простым методом, основанным на знании связи дуги и угла в геометрии окружности.
Предположим, что у нас есть окружность с центром O и радиусом r, а также известна дуга данной окружности, выраженная в радианах или градусах. Наша задача - найти угол между двумя лучами, образующими данную дугу на окружности.
Для решения этой задачи мы можем воспользоваться формулой, которая связывает длину дуги S, радиус r и угол α:
S = r * α
Для нахождения угла α по известной длине дуги S и радиусу r, достаточно разделить длину дуги на радиус:
α = S / r
Таким образом, мы можем легко определить угол между двумя лучами на окружности по известной дуге, используя простой метод. Данная формула может быть использована для решения различных задач, связанных с геометрией окружности.
Применение метода на практике

Представим, что у нас есть дуга окружности с известной длиной. Мы хотим найти угол, который соответствует этой дуге. Для этого мы можем использовать простой метод.
Для начала, мы измеряем длину дуги с помощью линейки или другого измерительного инструмента. Далее, мы должны знать радиус окружности, которой принадлежит дуга. Если радиус неизвестен, его можно измерить либо найти в задаче.
Затем мы вычисляем длину окружности по формуле: длина окружности = 2 * π * радиус, где π (пи) приближенно равно 3,14. Полученную длину окружности мы сравниваем с известной нам длиной дуги.
Исходя из этих данных, мы можем вычислить соответствующий угол, используя пропорцию: угол = (длина дуги / длина окружности) * 360°. Таким образом, мы получаем угол в градусах.
Применение этого метода позволяет найти угол по известной дуге без использования специализированных математических функций. Он может быть полезен в различных ситуациях, таких как строительство, геометрия, физика и другие области, где требуется определить угол по известным данным.
| Пример | Расчет угла |
|---|---|
| Дуга длиной 10 см | (10 / (2 * 3.14 * радиус)) * 360° |