Расчет вероятности с заданной плотностью распределения является важной задачей в теории вероятностей и математической статистике. Вероятностное распределение описывает, как вероятность нахождения случайной величины в определенном интервале значений связана с плотностью распределения. Это может быть полезно при изучении различных случайных процессов, а также при прогнозировании и принятии решений в различных сферах деятельности.
Подходы к вычислению вероятности с заданной плотностью распределения могут быть разнообразны, но существует эффективный способ, который позволяет получить точные результаты. Он основан на использовании интеграла, который позволяет вычислить площадь под кривой плотности распределения в заданном интервале значений.
Для использования этого способа необходимо знать плотность распределения и заданный интервал значений. Далее, с помощью математической формулы интеграла, можно вычислить вероятность нахождения случайной величины в этом интервале. Этот метод является точным и позволяет получить численное значение вероятности, которое можно использовать для различных статистических и аналитических целей.
Как вычислить вероятность с заданной плотностью распределения

Для вычисления вероятности с заданной плотностью распределения можно использовать интеграл от плотности распределения в заданном интервале значений. Интеграл от плотности распределения в заданном интервале дает вероятность попадания случайной величины в этот интервал.
Шаги для вычисления вероятности с заданной плотностью распределения:
- Определить функцию плотности распределения. Функция плотности распределения может быть задана аналитически или в виде таблицы значений.
- Определить интервал, в котором нужно найти вероятность. Интервал может быть задан конкретными значениями или выражен как неравенство.
- Вычислить интеграл от функции плотности распределения в заданном интервале значений.
- Полученное значение интеграла будет являться вероятностью попадания случайной величины в заданный интервал.
Эффективный способ расчета вероятности с заданной плотностью распределения позволяет точно определить вероятность попадания случайной величины в заданный интервал значений. Этот метод является основой для множества теоретических и практических задач, связанных с анализом и оценкой рисков, прогнозированием и моделированием различных событий.
Анализ функции плотности распределения
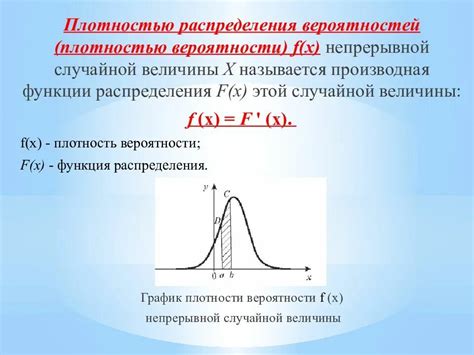
Функция плотности распределения играет важную роль в статистике и вероятностном анализе. Она позволяет определить вероятность того, что случайная величина примет определенное значение в заданном интервале.
Анализ функции плотности распределения включает в себя вычисление и исследование ее свойств. В первую очередь, необходимо проверить, что интеграл от функции плотности равен единице, так как общая площадь под кривой должна быть равна единице.
Можно также определить среднее значение и дисперсию случайной величины, используя функцию плотности распределения. Среднее значение является математическим ожиданием случайной величины, а дисперсия показывает, насколько случайная величина разбросана вокруг своего среднего значения.
При анализе функции плотности распределения важно также обратить внимание на форму кривой. Нормальное распределение имеет симметричную форму с пиком в центре, а унимодальные распределения имеют один пик. Многомодальные распределения имеют несколько пиков.
Для анализа функции плотности распределения можно использовать графические методы, такие как построение графика функции плотности или гистограммы, которая аппроксимирует функцию плотности. Также можно вычислять вероятности с помощью численных методов, таких как интегрирование численно-аналитических функций или метод Монте-Карло.
Важно учитывать, что функция плотности распределения существует только для непрерывных случайных величин. Для дискретных случайных величин используется функция вероятности, которая определяет вероятность получения конкретного значения.
Анализ функции плотности распределения является ключевым шагом при исследовании случайных величин и применении статистических методов. Он позволяет получить важную информацию о вероятностных характеристиках и форме распределения случайной величины.
Выбор метода численного интегрирования

Для вычисления вероятности с заданной плотностью распределения может потребоваться использование численных методов интегрирования. Основная идея таких методов заключается в аппроксимации площади под кривой плотности распределения интегралом от этой плотности.
При выборе метода численного интегрирования необходимо учитывать несколько факторов:
| Фактор | Значимость | Комментарий |
| Точность | Высокая | Метод должен обеспечивать достаточную точность вычислений, чтобы получить вероятность с нужной степенью точности. |
| Скорость | Высокая | Метод должен быть достаточно быстрым, чтобы вычисления не занимали слишком много времени. |
| Устойчивость | Высокая | Метод должен быть устойчивым к различным типам функций и не вызывать проблем с сходимостью при интегрировании. |
| Простота реализации | Высокая | Метод должен быть легко реализуемым и понятным в использовании, чтобы можно было применить его в практических задачах. |
| Возможность расширения | Желательная | Метод должен допускать различные модификации и расширения для решения задач с более сложными условиями или специфическими требованиями. |
На основе этих факторов можно выбрать подходящий метод численного интегрирования, такой как метод прямоугольников, метод тrapеций, метод Симпсона или другие. Важно учитывать особенности задачи и требования к вычислениям для определения оптимального метода.
Выбор метода численного интегрирования является важным этапом при вычислении вероятности с заданной плотностью распределения. Правильный выбор позволит получить точные и надежные результаты, а также сэкономить время и ресурсы при проведении вычислений.
Расчет вероятности с использованием метода Монте-Карло

Для расчета вероятности с использованием метода Монте-Карло необходимо выполнить следующие шаги:
- Сгенерировать большое количество случайных чисел, соответствующих заданной плотности распределения.
- Определить количество случайных чисел, которые удовлетворяют условию события.
- Вычислить отношение количества случайных чисел, удовлетворяющих условию, к общему количеству сгенерированных чисел.
Чем больше количество сгенерированных чисел, тем точнее будет расчет вероятности. Однако, следует учитывать, что метод Монте-Карло является приближенным и его точность зависит от количества сгенерированных чисел.
Использование метода Монте-Карло позволяет вычислить вероятность события с заданной плотностью распределения без необходимости вычисления интеграла или аналитического решения. Этот метод широко применяется в различных областях, таких как финансы, машинное обучение, статистика и другие, где требуется быстрый и эффективный расчет вероятностей.
Применение аппроксимации для упрощения расчетов
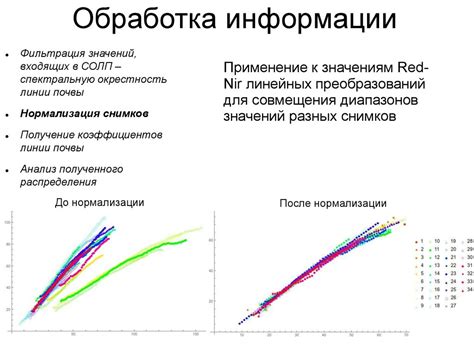
При расчете вероятности с заданной плотностью распределения может быть полезно использовать аппроксимацию для упрощения расчетов. Аппроксимация позволяет заменить сложную функцию плотности распределения более простым аналитическим выражением или приближенной формулой, что упрощает процесс вычислений и позволяет получить быстрые и точные результаты.
Одним из методов аппроксимации является разложение плотности распределения в ряд Тейлора. Этот метод основан на разложении функции в бесконечное число слагаемых, которые могут быть выражены в виде производных функции в заданной точке. При использовании разложения в ряд Тейлора, мы можем приблизить функцию плотности распределения заданного закона распределения с заданной точностью.
Другим методом аппроксимации является использование аппроксимационных формул, основанных на известных законах распределения, таких как нормальное, равномерное или экспоненциальное распределение. Эти формулы позволяют легко вычислять вероятности, используя известные параметры распределения и таблицы стандартных значений.
Применение аппроксимации значительно упрощает расчеты и позволяет сократить время, затрачиваемое на получение результатов. Однако, необходимо учитывать, что при использовании аппроксимации могут возникать погрешности, особенно при вычислении вероятностей в хвостах распределения. Поэтому, перед применением аппроксимации, необходимо внимательно оценить ее точность и сопоставить с требованиями задачи.
Таким образом, использование аппроксимации для упрощения расчетов позволяет сократить время и усилия, затрачиваемые на вычисление вероятностей с заданной плотностью распределения. Однако, необходимо быть аккуратным и проверять точность и качество аппроксимации, чтобы обеспечить достаточно точные результаты и избежать возможных погрешностей.
Использование графического метода для оценки вероятности
Основная идея графического метода заключается в построении графика плотности распределения и вычислении площадей под кривой. Вероятность события определяется как отношение площади под кривой в заданном диапазоне к общей площади под всей кривой.
Процесс использования графического метода для оценки вероятности может быть разделен на следующие шаги:
- Задайте функцию плотности распределения и определите интересующую вас область.
- Постройте график плотности распределения.
- Вычислите площадь под кривой в заданном диапазоне.
- Вычислите общую площадь под всей кривой.
- Определите вероятность события как отношение площади под кривой в заданном диапазоне к общей площади.
Графический метод позволяет наглядно представить вероятность события и сравнить ее с другими вероятностями. Он прост в использовании, даже для людей без математического образования. Однако, для более точных результатов, рекомендуется использовать другие статистические методы и инструменты.
Учет ограничений на переменные и параметры распределения
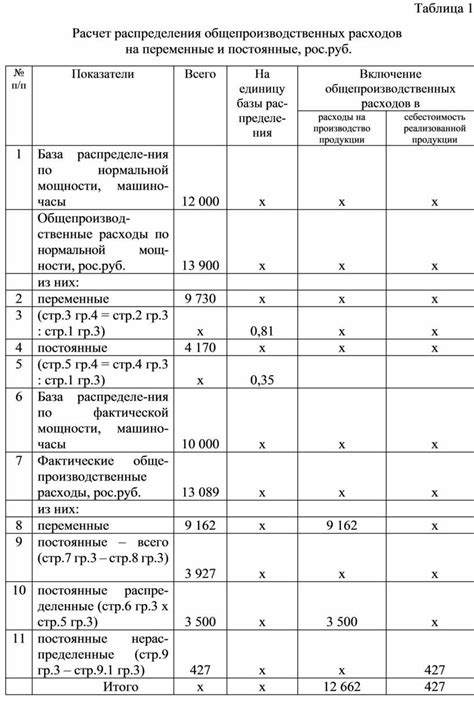
При вычислении вероятности с заданной плотностью распределения часто возникают ситуации, когда нужно учесть ограничения на переменные и параметры распределения. Это может быть необходимо, например, для моделирования социально-экономических процессов, где существуют ограничения на доходы или расходы индивидов, или для прогнозирования финансовых рынков с учетом границ риска.
Одним из эффективных способов учета ограничений является использование условной плотности распределения. Для этого вводится новая функция, которая учитывает ограничения и возвращает вероятность с заданными условиями.
Для расчета условной вероятности можно использовать табличный метод. На первом шаге строится таблица со значениями переменных и параметров, удовлетворяющими ограничениям. Затем по этой таблице расчитывается условная плотность распределения и вероятность с заданными условиями.
| Переменная | Ограничение | Значение |
|---|---|---|
| X | X > a | x1 |
| Y | Y < b | y1 |
| Параметр | Параметр = c | c1 |
После построения таблицы можно вычислить условную плотность распределения для заданных значений X, Y и параметра. Затем интегрируя эту плотность в соответствующих областях, получить вероятность с заданными условиями.
Такой подход позволяет учесть ограничения на переменные и параметры распределения, и эффективен в случаях, когда ограничения сложные или нелинейные. Однако стоит помнить, что использование условной плотности и табличного метода может занимать больше времени и ресурсов в сравнении с обычными методами расчета вероятности.
Сравнение эффективности различных методов расчета вероятности распределения
При расчете вероятности распределения с заданной плотностью, существуют различные методы, которые могут быть использованы. Каждый метод имеет свои особенности и эффективность в зависимости от конкретной задачи и объема данных.
Одним из основных методов расчета вероятности распределения является метод численного интегрирования. Этот метод основан на приближенном вычислении значения вероятности путем аппроксимации плотности распределения. В результате происходит разбиение области интегрирования на малые части и нахождение суммы вероятностей этих частей. Недостатком данного метода является большое количество вычислений, что может замедлить процесс при большом объеме данных.
Другим методом, часто используемым при расчете вероятности распределения, является метод Монте-Карло. Он основан на генерации случайных чисел и статистическом сопоставлении их с плотностью распределения. Данный метод позволяет получить приближенное значение вероятности с заданной точностью, однако трудоемкость вычислений может быть большой при большом числе генерируемых случайных чисел.
Также существуют методы аналитического расчета вероятности распределения, которые позволяют получить точное значение вероятности. Однако использование данных методов может быть ограничено сложностью математических выкладок и наличием аналитической формулы для плотности распределения.
В итоге, эффективный выбор метода расчета вероятности распределения зависит от конкретного случая и требуемой точности вычислений. Необходимо анализировать объем данных, сложность математических моделей и доступные вычислительные ресурсы для выбора наиболее оптимального метода расчета.