Цилиндр – это геометрическое тело, образованное поворотной фигурой, состоящей из окружности и прямой линии, проходящей через ее центр. Он является одним из базовых объектов в геометрии и находит практическое применение во многих сферах, включая архитектуру, инженерию и физику. Высота цилиндра – один из его главных параметров, который имеет решающее значение для его конструкции и способности хранить объем. Но как найти высоту цилиндра, если известны только его радиус и объем?
Для решения этой задачи нам понадобится использовать формулу для вычисления объема цилиндра и, опираясь на результат, выразить высоту цилиндра. Формула для вычисления объема цилиндра звучит следующим образом: V = π * R^2 * h, где V – объем цилиндра, π – число Пи, R – радиус окружности основания, h – высота цилиндра. Зная значения радиуса и объема, можно преобразовать эту формулу и найти высоту цилиндра.
Для начала, выразим высоту цилиндра через известные величины. Для этого разделим обе части формулы для объема цилиндра на π * R^2: h = V / (π * R^2). Таким образом, высоту цилиндра можно найти, разделив значение объема на произведение числа Пи и квадрата радиуса.
Как определить высоту цилиндра по радиусу и объему?

Высота цилиндра может быть определена по формуле:
Высота = Объем / Площадь основания
Для расчета высоты цилиндра по радиусу и объему необходимо знать значения радиуса и объема. Площадь основания цилиндра можно вычислить по формуле S = π * r^2, где π - число пи (около 3,14), r - радиус цилиндра.
Подставляя значения радиуса и объема в формулу, получаем:
Высота = Объем / (π * r^2)
Таким образом, зная значения радиуса и объема цилиндра, можно определить его высоту используя данную формулу.
Что такое цилиндр и как его характеризовать?

Цилиндр характеризуется несколькими параметрами:
- Радиус - это расстояние от центра основания до любой точки на его окружности. Обозначается буквой "r".
- Диаметр - это двойной радиус, то есть расстояние между двумя точками на окружности одного основания через его центр. Обозначается буквой "d".
- Высота - это расстояние между плоскостями оснований цилиндра. Обозначается буквой "h".
- Объем - это мера заполняемого цилиндром пространства. Обозначается буквой "V".
Чтобы найти высоту цилиндра по радиусу и объему, можно использовать формулу:
h = V / (π * r^2)
Формула для расчета радиуса цилиндра
Для расчета радиуса цилиндра по известному объему и высоте можно использовать следующую формулу:
Радиус (r) = √ (3 * V / (π * h))
Где:
- r - радиус цилиндра
- V - объем цилиндра
- h - высота цилиндра
- π - число Пи (приблизительно равное 3.14159)
Таким образом, зная объем и высоту цилиндра, можно легко вычислить его радиус, используя данную формулу.
Формула для расчета объема цилиндра
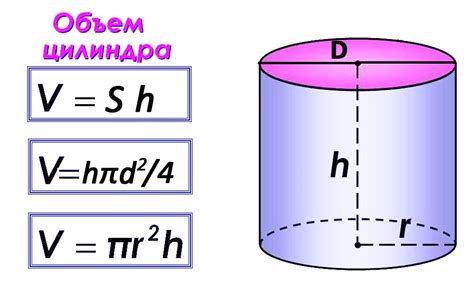
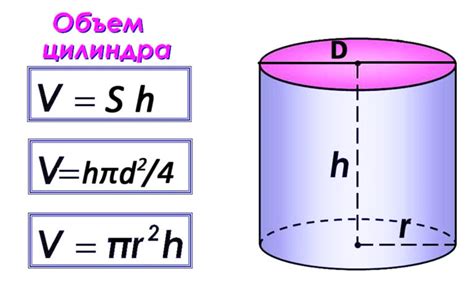
Объем цилиндра можно определить по следующей формуле:
V = π * r2 * h
Где:
- V - объем цилиндра;
- π (пи) - математическая константа, примерное значение которой равно 3.14159;
- r - радиус цилиндра;
- h - высота цилиндра.
Используя данную формулу, можно легко определить объем цилиндра по известным значениям его радиуса и высоты. Эта формула применяется в различных сферах науки и техники, где требуется расчет объемов цилиндрических объектов.
Как определить высоту цилиндра по радиусу и объему?

Для этого нужно использовать формулу для объема цилиндра, которая связывает радиус, высоту и объем. Формула для объема цилиндра выглядит следующим образом:
объем = площадь основания * высота цилиндра
Раскрывая эту формулу, мы получаем следующее равенство:
объем = π * радиус^2 * высота цилиндра
Отсюда можно выразить высоту цилиндра:
высота цилиндра = объем / (π * радиус^2)
Например, если известны радиус цилиндра и его объем, можно подставить данные значения в формулу и вычислить высоту.
Давайте посмотрим на пример:
| Радиус (см) | Объем (см³) | Высота (см) |
|---|---|---|
| 5 | 100 | 4 |
В этом случае, если радиус цилиндра равен 5 см, а его объем равен 100 см³, то подставив эти значения в формулу, мы получим, что высота цилиндра равна 4 см.
Используя указанные формулы, вы можете определить высоту цилиндра по радиусу и объему. Убедитесь, что соблюдаете правильные единицы измерения во всех расчетах, чтобы получить корректный результат.