Высота прямоугольного треугольника является одной из его важных характеристик. Она позволяет определить расстояние от одного из его углов до основания. Если у вас есть прямоугольный треугольник, у которого известна только гипотенуза, вы можете легко найти его высоту, используя формулу, основанную на теореме Пифагора.
Теорема Пифагора утверждает, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов его катетов. В данном случае, чтобы найти высоту, мы будем использовать формулу h = a * b / c, где h - высота, a и b - катеты, c - гипотенуза треугольника.
Давайте рассмотрим пример. Предположим, у нас есть прямоугольный треугольник с гипотенузой, равной 5, и катетом, равным 3. Чтобы найти высоту, мы должны подставить эти значения в формулу: h = 3 * b / 5. Выразив высоту, мы получаем следующий результат: h = 3 * 4 / 5 = 12 / 5 = 2.4.
Как определить высоту прямоугольного треугольника
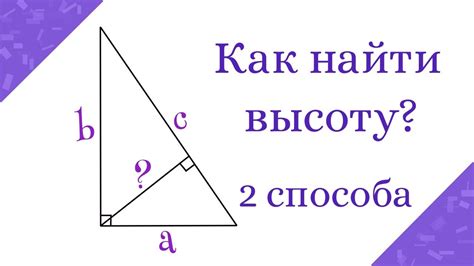
Высота прямоугольного треугольника может быть найдена с использованием известной гипотенузы (стороны, противолежащей прямому углу) и одного из катетов (сторон, образующих прямой угол).
Формула для нахождения высоты прямоугольного треугольника:
Высота = (Катет * Гипотенуза) / Квадратный корень из (Катет^2 + Гипотенуза^2)
Для понимания данной формулы можно использовать пример: рассмотрим прямоугольный треугольник со сторонами 3, 4 и 5. Гипотенуза этого треугольника равна 5. Пусть один из катетов равен 3. Тогда для нахождения высоты треугольника применим указанную формулу:
Высота = (3 * 5) / Квадратный корень из (3^2 + 5^2)
Высота = 15 / Квадратный корень из (9 + 25)
Высота = 15 / Квадратный корень из 34
Высота ≈ 15 / 5,83 ≈ 2,57
Таким образом, высота прямоугольного треугольника с катетами 3 и 4 и гипотенузой 5 составляет около 2,57.
Теперь вы знаете, как определить высоту прямоугольного треугольника с известной гипотенузой. Эта информация может быть полезной при решении различных математических задач и практических применений.
Методы нахождения высоты при известной гипотенузе

1. Формула площадей
Один из способов найти высоту прямоугольного треугольника - использовать формулу площадей. Площадь прямоугольного треугольника вычисляется по формуле S = (a * b) / 2, где S - площадь, a и b - катеты, а самая длинная сторона (гипотенуза) является высотой.
2. Теорема Пифагора
Еще один метод нахождения высоты прямоугольного треугольника - использовать теорему Пифагора. Если известны длины катетов a и b, а гипотенузу обозначить как c, то высота будет равна h = (a * b) / c.
3. Тригонометрические функции
Третий метод основан на использовании тригонометрических функций. Если известна гипотенуза c и угол α между гипотенузой и катетом a, то высота будет равна h = c * sin(α).
Выбор определенного метода зависит от доступных вам данных и условий задачи. Убедитесь в правильности выбранного метода перед приступлением к решению и используйте его для нахождения высоты прямоугольного треугольника при известной гипотенузе.