Косинус и синус - это две важные тригонометрические функции, которые используются для вычислений в различных областях науки и техники. Однако, иногда возникает необходимость найти синус, зная только косинус и промежуток значений, в котором находится угол. Следуя данной инструкции в 7 шагов, вы сможете легко определить значение синуса.
Шаг 1: Проверьте, находится ли угол в главных областях определения синуса и косинуса. Главный промежуток значений для синуса и косинуса находится в диапазоне от -1 до 1.
Шаг 2: Определите, какое значение косинуса вам известно. Обозначим его как cos(x).
Шаг 3: Используя известное значение косинуса, найдите значение синуса. Для этого воспользуйтесь формулой синуса по косинусу: sin(x) = ± sqrt(1 - cos^2(x)). Помните, что значение синуса может быть положительным или отрицательным в зависимости от промежутка.
Шаг 4: Если угол x находится в первом или втором квадранте (0° ≤ x ≤ 180°), то значение синуса будет положительным. Если же угол x находится в третьем или четвертом квадранте (180°
Шаг 5: Если вам известен промежуток значений, в котором находится угол, проверьте его. Если значение синуса не попадает в этот промежуток, значит, вы выбрали неправильное значение для косинуса.
Шаг 6: Повторите расчет, используя другие значения косинуса, если необходимо.
Шаг 7: Проверьте свои вычисления, используя таблицу значений синуса и косинуса или специализированный калькулятор.
Шаг 1. Определение косинуса угла

Для определения косинуса угла необходимо знать значение двух сторон прямоугольного треугольника, а именно гипотенузы и прилежащей к данному углу стороны.
Формула для нахождения косинуса угла выглядит следующим образом:
| Косинус угла (cos) | = | Прилежащая сторона | / | Гипотенуза |
|---|
Зная значения прилежащей стороны и гипотенузы прямоугольного треугольника, можно легко вычислить косинус угла. Полученное значение косинуса будет использовано в дальнейших шагах для нахождения синуса по косинусу и промежутку.
Шаг 2. Нахождение промежуточного значения

Для нахождения промежуточного значения синуса по заданному косинусу и промежутку необходимо использовать формулу обратной функции синуса. Эта формула позволяет найти значение угла, при котором синус равен заданному косинусу.
Для начала, найдите обратную функцию синуса на вашем калькуляторе или в таблице. Для обратной функции синуса используется обозначение arcsin или sin-1.
Затем, подставьте заданный косинус в формулу обратной функции синуса и решите уравнение, чтобы найти значение угла.
Промежуточное значение синуса будет равно синусу найденного угла. Запишите это значение для дальнейшего использования.
Шаг 3. Определение знака синуса и косинуса
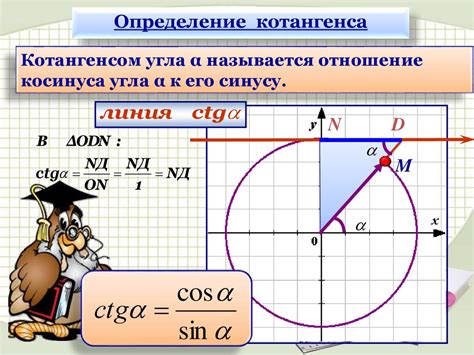
После того, как вы нашли значение косинуса и промежуток, необходимо определить знаки синуса и косинуса для данного значения.
Для этого рекомендуется использовать таблицу знаков на основе четвертей координатной плоскости. Выделите два столбца в таблице. В первом столбце укажите промежутки, а во втором - знаки синуса и косинуса.
| Промежуток | Знак синуса и косинуса |
|---|---|
| 0° - 90° | + |
| 90° - 180° | - |
| 180° - 270° | - |
| 270° - 360° | + |
Определите, в какой из указанных диапазонов находится значение косинуса. Если значение косинуса положительное, то синус будет иметь тот же знак. Если значение косинуса отрицательное, то синус будет иметь противоположный знак.
Таким образом, зная знак косинуса и промежуток, можно определить знак синуса.
Шаг 4. Поиск значений синуса и косинуса в таблице
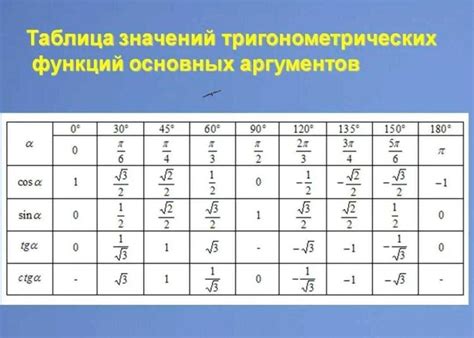
После определения значений косинуса и промежутка, настало время найти значения синуса. Для этого нам понадобится таблица значений синуса и косинуса.
Таблица значений синуса и косинуса представляет собой список углов и соответствующих им значений синуса и косинуса. Такая таблица может быть найдена в учебниках математики или физики, а также в справочниках и онлайн-ресурсах.
Используя значения косинуса, найденные на предыдущем шаге, вам нужно найти соответствующие им значения синуса в таблице. Обратите внимание, что значения синуса и косинуса имеют отношение к одному и тому же углу и различаются только знаком. Если значение косинуса положительное, то значение синуса будет отрицательным, и наоборот.
Найденные значения синуса и косинуса могут быть округлены до нескольких десятичных знаков в соответствии с заданными требованиями точности. Округление может быть выполнено с помощью стандартных правил округления цифр.
Пример:
Допустим, у нас есть значение косинуса равное 0.5 и мы хотим найти соответствующее значение синуса в таблице. Если мы находим значение косинуса в таблице, мы обнаружим, что угол, для которого косинус равен 0.5, равен 60 градусам или π/3 радианам. Значение синуса для этого угла будет -√3/2.
Таким образом, значения синуса и косинуса, найденные в таблице, помогут нам точно определить значения функций синуса и косинуса для заданного угла и промежутка.
Шаг 5. Интерполяция значений синуса и косинуса
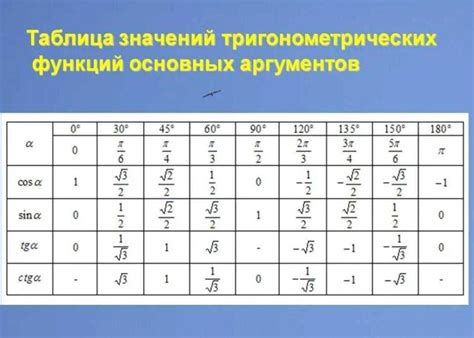
Для начала, нам понадобятся значения синуса и косинуса для двух заданных точек. Допустим, у нас есть значения sin(a) и cos(a) для точки "a" и значения sin(b) и cos(b) для точки "b".
Теперь мы можем использовать формулу линейной интерполяции для нахождения промежуточных значений:
sin(x) = sin(a) + (sin(b) - sin(a)) * [(x - a) / (b - a)]
cos(x) = cos(a) + (cos(b) - cos(a)) * [(x - a) / (b - a)]
Где "x" - это значение внутри промежутка между точками "a" и "b". Он может быть любым числом, находящимся между значениями "a" и "b".
Используя эти формулы, мы можем находить значения синуса и косинуса для любого значения внутри заданного промежутка. Это очень полезно, если нам нужно найти значение синуса или косинуса для точки, которая не находится в таблице значений.
После того, как мы найдем все промежуточные значения, мы можем использовать их для построения графика синуса и косинуса для заданного промежутка.
Шаг 6. Нахождение синуса по косинусу в заданном промежутке
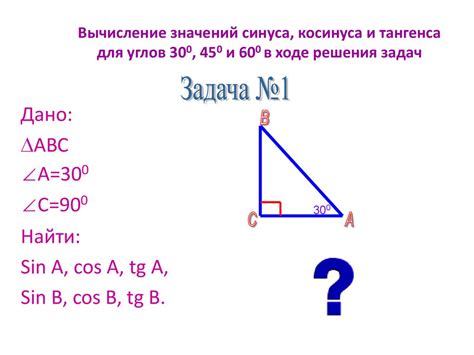
Если вам известен косинус угла в заданном промежутке, вы также можете найти синус этого угла. Для этого необходимо выполнить следующие действия:
- Определите промежуток, в котором находится косинус вашего угла. Например, если косинус равен 0,5, то он находится в промежутке от 0 до 1.
- Используя тригонометрическую окружность или таблицу значений, найдите все значения углов, у которых косинус находится в указанном промежутке. Обычно промежуток [-π/2, π/2] отражает все возможные значения синуса и косинуса.
- Выберите значение угла из найденных в предыдущем шаге. Обозначим его как A.
- Определите знак синуса в зависимости от квадранта, в котором находится угол A. Например, если A находится в первом квадранте, то синус будет положительным.
- Вычислите синус угла A, используя формулу синуса: sin(A) = √(1 - cos²(A)).
Теперь у вас есть значение синуса для заданного косинуса угла в указанном промежутке.