В равнобедренном треугольнике одна сторона и два угла равны между собой. Один из углов равнобедренного треугольника всегда острый, а другой тупой. Синус тупого угла в равнобедренном треугольнике можно найти, зная длины сторон треугольника и значение синуса острого угла.
Для решения этой задачи используется теорема синусов. Согласно этой теореме, отношение длины стороны к синусу противоположного ей угла в треугольнике равно одному и тому же числу для всех сторон и синусов. Таким образом, можно записать формулу:
a/sin(A) = b/sin(B) = c/sin(C)
где a, b и c - длины сторон треугольника, A, B и C - величины соответствующих углов, sin(A), sin(B) и sin(C) - синусы этих углов.
Для нахождения синуса тупого угла в равнобедренном треугольнике необходимо знать длины сторон треугольника и значение синуса острого угла. Подставьте известные значения в формулу теоремы синусов, чтобы найти синус тупого угла.
Изучение синуса тупого угла
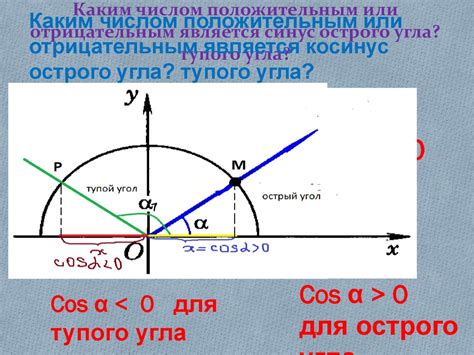
Синус тупого угла в равнобедренном треугольнике можно найти, применив определение синуса и учитывая его свойства.
Синус угла в треугольнике определяется как отношение длины противолежащего катета к гипотенузе, то есть sin(угол) = длина противолежащего катета / длина гипотенузы.
В равнобедренном треугольнике противолежащий катет также является основанием. Чтобы найти синус тупого угла, нужно быть внимательным и использовать особенности равнобедренного треугольника.
| Свойства равнобедренного треугольника: | Формула для нахождения синуса тупого угла: |
|---|---|
| Две стороны равны | sin(угол) = длина основания / длина гипотенузы |
| Два угла при основании равны | sin(угол) = sin(оппозитный угол при основании) |
Изучение синуса тупого угла в равнобедренном треугольнике поможет в объяснении геометрических закономерностей и решении задач на построение, нахождение сторон и углов произвольных равнобедренных треугольников.
Определение и свойства синуса

Синус угла θ обозначается как sin(θ) или sin θ. Значение синуса угла θ всегда лежит в пределах от -1 до 1. Геометрически, синус угла можно представить как отношение длины противоположной стороны к длине гипотенузы.
Свойства синуса:
- Синус угла равен 1 при значении угла π/2 радиан или 90 градусов.
- Синус угла равен 0 при значении угла 0 радиан или 0 градусов.
- Синус угла равен -1 при значении угла -π/2 радиан или -90 градусов.
- Синус угла в первой четверти положителен.
- Синус угла во второй четверти положителен.
- Синус угла в третьей четверти отрицателен.
- Синус угла в четвертой четверти отрицателен.
- Синус угла θ равен синусу суплементарного угла (дополнение θ до прямого угла).
Как найти тупой угол в равнобедренном треугольнике
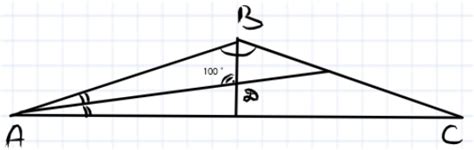
Для нахождения тупого угла в равнобедренном треугольнике можно использовать следующий метод:
- Найдите один из острых углов равнобедренного треугольника.
- Найдите значение этого угла, используя теорему о сумме углов треугольника (сумма углов треугольника равна 180 градусов).
- Вычтите значение найденного угла из 180 градусов. Полученное значение будет тупым углом равнобедренного треугольника.
Например, если один из острых углов равнобедренного треугольника равен 60 градусов, то тупой угол будет равен 180 - 60 = 120 градусов.
Имейте в виду, что этот метод применим только для равнобедренных треугольников.
Формула нахождения синуса тупого угла

Для нахождения синуса тупого угла в равнобедренном треугольнике существует специальная формула:
1. Найдите значение одного из острых углов треугольника, используя обычные формулы нахождения синуса или косинуса.
2. Вычислите значение синуса найденного угла, применив формулу синуса для тупого угла:
- Синус тупого угла равен синусу его дополнения до прямого угла. Дополнение тупого угла образуется окружностью с центром в вершине треугольника, проходящей через его основание.
- Таким образом, синус тупого угла равен синусу острого угла, смежного с основанием равнобедренного треугольника, или синусу его суплемента.
- Формула: sin(t) = sin(180 - t), где t - значение острого угла, найденного на первом шаге.
- Вычислите синус тупого угла, подставив значение острого угла в формулу.
Теперь вы знаете, как найти синус тупого угла в равнобедренном треугольнике, используя специальную формулу. Помните, что для корректных вычислений необходимо использовать значения углов в градусах или радианах, в зависимости от используемой формулы.