Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны и равны по длине. В параллелограмме также есть углы, некоторые из которых могут быть прямыми, а некоторые - не прямыми. Как найти синус одного из углов параллелограмма?
Синус угла определяется отношением противоположной стороны угла к гипотенузе прямоугольного треугольника, образованного этой стороной и одной из сторон параллелограмма. Чтобы найти синус угла в параллелограмме, нужно разделить противоположную сторону на гипотенузу и вычислить значение синуса с помощью тригонометрической функции.
Важно помнить, что для вычисления синуса угла в параллелограмме необходимо знать длину противоположной стороны и длину гипотенузы прямоугольного треугольника, образованного этой стороной и одной из сторон параллелограмма. Эти значения можно получить, зная другие параметры параллелограмма или используя геометрические свойства фигуры.
Синус угла в параллелограмме: правила и формулы
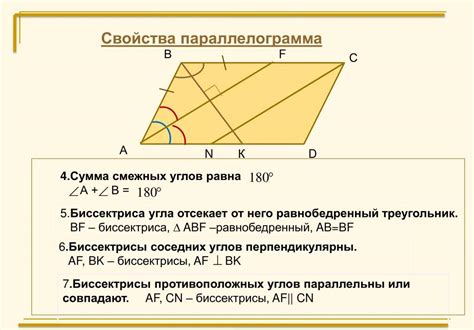
Для нахождения синуса угла в параллелограмме применяются следующие правила и формулы:
- При заданном параллелограмме находим длину противолежащей стороны угла либо длину диагонали;
- Делим длину противолежащей стороны угла на длину диагонали;
- Полученное значение является синусом угла в параллелограмме.
Формула для вычисления синуса угла в параллелограмме:
sin(угол) = длина противолежащей стороны / длина диагонали
Пример:
- Пусть задан параллелограмм ABCD, где AB = 10 см и AC = 6 см;
- Найдем синус угла A:
- Согласно формуле, sin(A) = AB / AC = 10 / 6 = 1.67
- Синус угла A в параллелограмме ABCD равен 1.67.
Знание синуса угла в параллелограмме позволяет решать задачи, связанные с нахождением длин сторон и углов параллелограмма, а также проведением конструкций и решением геометрических задач.
Понятие параллелограмма
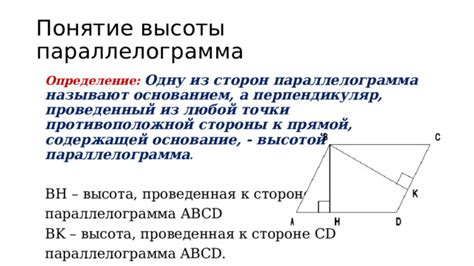
- Противоположные углы параллелограмма равны между собой.
- Сумма углов параллелограмма равна 360 градусов (или двум прямым углам).
- Диагонали параллелограмма делятся пополам.
Параллелограмм может быть прямоугольным, когда все его углы прямые и стороны равны попарно. В этом случае он называется прямоугольным параллелограммом или прямоугольником.
Также существуют специальные типы параллелограммов, такие как квадрат (параллелограмм со всеми сторонами и углами равными) и ромб (параллелограмм с равными сторонами).
Зная свойства параллелограмма, можно решать различные задачи, связанные с нахождением его углов, сторон, периметра и площади.
Основные свойства параллелограмма
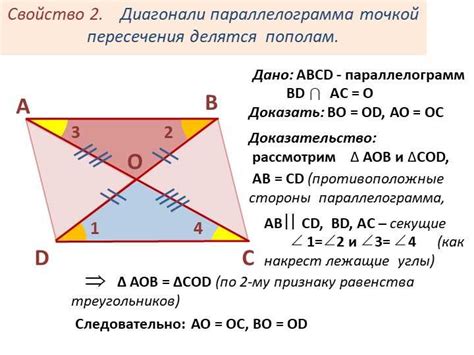
Основные свойства параллелограмма:
- Противоположные стороны параллельны и равны по длине.
- Противоположные углы параллельны и равны по мере.
- Сумма углов параллелограмма равна 360 градусов.
- Диагонали параллелограмма делятся пополам.
- Каждое основание параллелограмма является средним линиям для другого основания.
Зная эти свойства параллелограмма, мы можем использовать их для решения различных задач. Например, для нахождения синуса угла в параллелограмме можно использовать соотношения сторон и углов параллелограмма.
Определение синуса угла

Для определения синуса угла в параллелограмме, необходимо знать значения длин сторон и углов фигуры. Найдите две стороны параллелограмма, между которыми находится данный угол. Затем примените следующую формулу:
- Синус угла = Противолежащая сторона / Гипотенуза
Противолежащая сторона - это сторона параллелограмма, противоположная данному углу. Гипотенуза - это диагональ параллелограмма, которая проходит через данный угол.
После нахождения значения синуса угла, его можно использовать для решения различных задач, связанных с параллелограммами, таких как нахождение площади фигуры или длины сторон.
Зависимость синуса угла от сторон параллелограмма
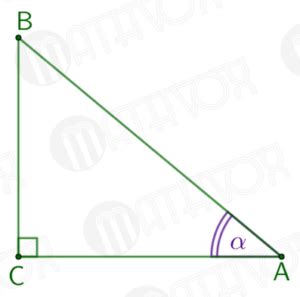
В параллелограмме, угол которого обозначен как α, можно найти зависимость синуса этого угла от длин его сторон.
Для начала рассмотрим параллелограмм с основаниями a и b, и высотой h, проведенной из угла между этими основаниями.
Так как синус угла α равен отношению противоположной стороны к гипотенузе, можно записать следующее соотношение:
sin(α) = h/b
Рассмотрим также параллелограмм с диагоналями p и q, и углом между ними β.
Аналогично, синус угла β равен отношению противоположной стороны к гипотенузе:
sin(β) = h/q
Таким образом, если нам заданы длины сторон и диагоналей параллелограмма, мы можем найти синусы всех его углов, используя приведенные зависимости.
Формула для нахождения синуса угла в параллелограмме

Для нахождения синуса угла в параллелограмме необходимо знать значения двух сторон параллелограмма и значение между ними опирающегося угла. Формула для нахождения синуса угла в параллелограмме выглядит следующим образом:
sin(угол) = (длина стороны A × длина стороны B × sin(угол между сторонами A и B)) / (площадь параллелограмма)
Здесь sin обозначает синус угла, угол - искомый угол, длина стороны A и длина стороны B - длины двух сторон параллелограмма, угол между сторонами A и B - угол, образованный двумя сторонами параллелограмма, и площадь параллелограмма - площадь данного параллелограмма.
Используя данную формулу, можно легко найти значение синуса угла в параллелограмме и использовать его для решения различных задач и проблем, связанных с параллелограммами.
Пример расчета синуса угла в параллелограмме
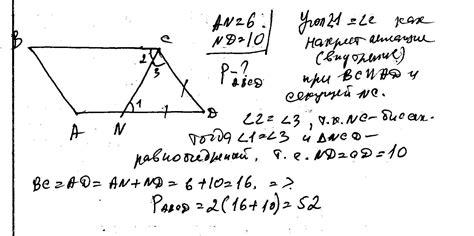
Для расчета синуса угла в параллелограмме необходимо знать длины двух векторов, образующих данный угол, а также угол между ними.
Представим, что у нас есть параллелограмм ABCD, где угол B равен заданному углу. Длины векторов AB и BC известны и равны, например, a и b соответственно.
Для вычисления синуса угла B воспользуемся формулой:
sin(B) = (a × b) / (|a| × |b|)
Где × - это скалярное произведение векторов, а |a| и |b| - длины векторов.
Зная значения a и b, а также длины векторов, мы можем расчитать значение синуса угла B.
Например, если длина вектора AB равна 5, а длина вектора BC равна 6, то сначала найдем sкалярное произведение векторов AB и BC:
(a × b) = |AB| × |BC| × cos(B)
(a × b) = 5 × 6 × cos(B)
(a × b) = 30 × cos(B)
Затем найдем длины векторов |AB| и |BC|:
|a| = |AB| = 5
|b| = |BC| = 6
И, наконец, расчитаем значение синуса угла B:
sin(B) = (a × b) / (|a| × |b|)
sin(B) = (30 × cos(B)) / (5 × 6)
sin(B) = 30 × cos(B) / 30
sin(B) = cos(B)
Таким образом, в данном примере мы получили, что синус угла B равен косинусу этого же угла.
Графическое представление синуса угла в параллелограмме

Синус угла в параллелограмме представляет собой отношение длины противолежащей стороны к длине диагонали. Графическое представление этого соотношения может помочь лучше понять и визуализировать его.
Для создания графического представления синуса угла в параллелограмме, мы можем нарисовать параллелограмм ABCD:
- Выбираем точку A в любом месте и называем её A.
- С помощью линейки и угольника проводим две параллельные линии от точки A. Называем эти линии AD и AB.
- Выбираем точку D на линии AD и точку B на линии AB.
- Проводим диагональ AC от точки A до точки C, которая является пересечением диагоналей AD и AB.
В результате получаем параллелограмм ABCD, в котором угол BAC является исследуемым углом.
Чтобы найти синус угла BAC, измеряем длину противолежащей стороны AC и длину диагонали AD. Затем применяем формулу синуса:
sin(BAC) = AC / AD
где AC - длина противолежащей стороны, AD - длина диагонали.
Таким образом, графическое представление синуса угла в параллелограмме помогает наглядно представить соотношение между длиной противолежащей стороны и длиной диагонали, и дает возможность вычислить значение синуса угла с помощью измерений.
Применение на практике: решение задач с использованием синуса угла в параллелограмме
Рассмотрим некоторые примеры задач, в которых можно использовать синус угла в параллелограмме.
Пример 1:
Дан параллелограмм ABCD, в котором известны длины сторон AB и BC. Нужно найти синус угла B.
Решение:
Известно, что в параллелограмме противоположные углы равны. Поэтому угол B равен углу D.
Также известно, что противоположные стороны параллелограмма параллельны и равны по длине.
Используем формулу синуса:
sin(B) = AB / BC.
Подставляем известные значения:
sin(B) = AB / BC.
sin(B) = 5 / 8.
Таким образом, синус угла B в параллелограмме ABCD равен 5/8.
Пример 2:
Дан параллелограмм ABCD, в котором известен угол B и длина стороны AB. Нужно найти длину стороны BC.
Решение:
В параллелограмме противоположные углы равны, поэтому угол B равен углу D.
Используем формулу синуса:
sin(B) = AB / BC.
Переставляем слагаемые:
BC = AB / sin(B).
Подставляем известные значения:
BC = AB / sin(B).
Таким образом, длина стороны BC равна AB / sin(B).
Как видно из данных примеров задач, знание синуса угла в параллелограмме может быть полезным при решении различных проблем, связанных с определением сторон или углов параллелограмма.