Треугольник - одна из самых простых и изучаемых фигур в геометрии. Как правило, для полного определения треугольника нам нужно знать все его стороны и углы. Однако, иногда у нас есть только некоторая часть информации, и мы должны найти остальные углы. В этой статье мы рассмотрим, как найти углы треугольника, если известны его стороны и угол.
Прежде чем мы начнем, давайте вспомним основные понятия. Угол - это область плоскости, ограниченная двумя лучами, которая измеряется в градусах. Треугольник имеет три угла, и сумма всех его углов всегда равна 180 градусов. Для нахождения неизвестного угла нам понадобится знание других углов или сторон треугольника.
Если у нас есть треугольник с известными сторонами и углом, то мы можем применить законы тригонометрии для нахождения неизвестных углов. Например, если у нас есть треугольник со сторонами a, b и c, и известен угол между сторонами a и b, то мы можем использовать закон косинусов для нахождения неизвестного угла.
Определение углов треугольника
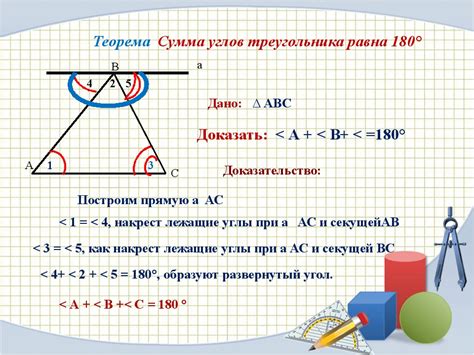
Углы треугольника могут быть разделены на три категории:
1. Острый угол - угол, меньший 90 градусов.
2. Прямой угол - угол, равный 90 градусов.
3. Тупой угол - угол, больший 90 градусов, но меньший 180 градусов.
Определение углов треугольника может быть выполнено с использованием различных формул и правил, включая теорему синусов, теорему косинусов и теорему о сумме углов треугольника. Используя данные о сторонах треугольника и известные углы, можно определить оставшиеся углы треугольника.
Знание углов треугольника позволяет решать множество задач и применять треугольники в различных областях науки и практики, включая геометрию, физику, строительство, навигацию и другие.
Зависимость углов треугольника от сторон

Углы треугольника зависят от длин его сторон. В общем случае, для определения углов треугольника по сторонам необходимо использовать теорему косинусов. Теорема косинусов гласит, что в треугольнике с сторонами a, b и c, угол A против стороны a можно найти по формуле:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
Аналогично можно найти углы B и C по соответствующим сторонам и другим формулам. Зная значения всех сторон треугольника, можно найти все его углы.
Также, если известны все углы треугольника, можно использовать тригонометрические функции для нахождения сторон. Например, для нахождения стороны a можно использовать формулу:
a = sqrt(b^2 + c^2 - 2 * b * c * cos(A))
Таким образом, углы треугольника и их зависимость от сторон являются важными характеристиками треугольника и позволяют определить его форму и размеры.
| Угол | Формула |
|---|---|
| A | cos(A) = (b^2 + c^2 - a^2) / (2 * b * c) |
| B | cos(B) = (a^2 + c^2 - b^2) / (2 * a * c) |
| C | cos(C) = (a^2 + b^2 - c^2) / (2 * a * b) |
Формулы для вычисления углов треугольника
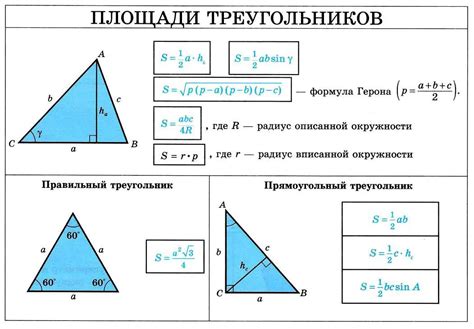
Вычисление углов треугольника может быть осуществлено с использованием различных формул, основанных на известных сторонах и угле треугольника. Ниже приведены основные формулы для нахождения углов треугольника:
| Формула | Описание |
|---|---|
| 1. Формула синусов | Углы треугольника могут быть найдены с использованием формулы синусов: |
| 2. Формула косинусов | Углы треугольника также могут быть вычислены с использованием формулы косинусов: |
| 3. Формула тангенсов | Третья формула, используемая для вычисления углов треугольника, это формула тангенсов: |
Используя данные формулы, можно легко вычислить значения углов треугольника, зная длины его сторон и угол.
Важно помнить, что существуют определенные условия, которым должен соответствовать треугольник, чтобы данные формулы были применимы. Например, сумма всех углов треугольника должна быть равна 180 градусам.
Формулы для вычисления углов треугольника являются одним из основных инструментов геометрии, позволяющих определить форму и размеры треугольника на основе имеющихся данных.
Примеры решения задач по нахождению углов треугольника
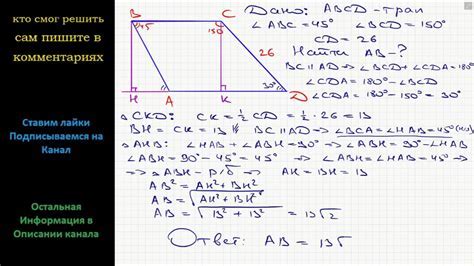
Задачи, связанные с нахождением углов треугольника, часто встречаются в геометрии и математике. Для решения таких задач существует несколько подходов и формул.
Один из самых простых способов – использование теоремы косинусов. Если известны длины всех сторон треугольника (a, b, c), то угол α, противолежащий стороне a, можно найти с помощью следующей формулы:
cos α = (b² + c² - a²) / (2bc)
Аналогично можно найти углы β и γ, используя стороны b, c и c, a соответственно.
Другим способом решения задачи является использование формулы синусов. Если известны длины всех сторон треугольника (a, b, c), а также углы α, β и γ, то можно найти синусы этих углов с помощью следующих формул:
sin α = a / c
sin β = b / c
sin γ = a / b
Из этих формул можно найти значения углов α, β и γ с помощью тригонометрических таблиц или калькулятора.
Также можно использовать теорему синусов для нахождения углов треугольника. Если известны длины двух сторон треугольника (a, b) и между ними известный угол γ, то можно найти углы α и β с помощью следующих формул:
sin α = (a * sin γ) / b
sin β = (b * sin γ) / a
Приведенные выше примеры демонстрируют различные способы решения задач по нахождению углов треугольника. В зависимости от доступных данных и требуемых результатов можно использовать тот или иной подход. Важно помнить, что при решении таких задач необходимо быть внимательным и аккуратным, чтобы избежать ошибок и получить правильный ответ.
В данной статье мы рассмотрели способы нахождения углов треугольника по заданным сторонам и углу.
Если известны все три стороны треугольника, то можно воспользоваться формулами для нахождения углов через косинусы.
Если известны две стороны и угол между ними, то можно применить теорему косинусов для нахождения третьей стороны, а затем воспользоваться формулами для нахождения углов по сторонам.
Если известны две стороны и угол противолежащий одной из них, то можно применить тангенс угла, воспользоваться формулой для нахождения третьей стороны и затем воспользоваться формулами для нахождения углов по сторонам.
Зная все углы треугольника, можно определить его тип: остроугольный, прямоугольный или тупоугольный.
Знание формул для нахождения углов по сторонам и углу позволяет решать разнообразные задачи, связанные с треугольниками, в том числе на практике, в геометрии и строительстве.


