Функции и графики являются одним из основных тематических разделов в программе обучения математике на ОГЭ. Понимание связи между функциями и графиками играет важную роль в успешной сдаче экзамена и решении задач на построение графиков. Функции, как математические объекты, описывают зависимость одной величины от другой и могут быть представлены в виде уравнений или графиков.
Когда мы говорим о графике функции, мы имеем в виду геометрическое представление этой функции. Всякий раз, когда строится график функции на плоскости, каждое значение независимой переменной соответствует определенному значению зависимой переменной. Таким образом, мы видим, как меняется зависимая переменная в зависимости от независимой. График представляет собой множество точек, которые соединены линиями или кривыми.
Функциональный подход к изучению математики позволяет нам анализировать различные типы функций и их графики. Например, линейная функция имеет простой график в виде прямой линии, квадратичная функция может иметь форму параболы, а тригонометрические функции могут иметь сложные и повторяющиеся графики. Понимание таких различий позволяет нам представить функции и их графики как взаимосвязанные объекты, которые помогают нам визуально представить математические концепции.
Как функции и графики связаны на ОГЭ по прямой
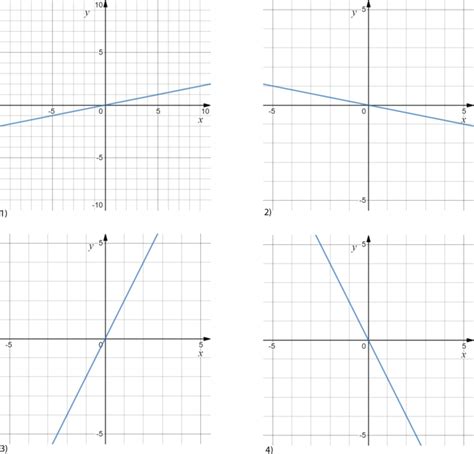
Функция представляет собой математическую зависимость, которая связывает каждому элементу одного множества (аргументу) элемент другого множества (значение). На ОГЭ по прямой рассматриваются линейные функции, которые задаются уравнением вида y = kx + b, где k и b - это числа, а x и y - это переменные.
| Тип функции | График на координатной плоскости | Общий вид уравнения |
|---|---|---|
| Прямая, проходящая через начало координат |  | y = kx |
| Прямая, параллельная оси ординат |  | x = a |
| Прямая, параллельная оси абсцисс |  | y = a |
| Прямая, не проходящая через начало координат |  | y = kx + b |
На ОГЭ по прямой задачи сводятся к определению характеристик линейных функций, таких как угловой коэффициент, точки пересечения с осями координат, а также определению уравнения прямой по ее графику.
Знание связи между функциями и графиками является ключевым для успешной подготовки и прохождения ОГЭ по математике. Поэтому следует уделить достаточно времени изучению этой темы и отработке навыков по ее применению в различных задачах.
Математика на ОГЭ: функции и графики

Один из разделов заданий по математике на ОГЭ связан с функциями и графиками. В данном разделе школьнику предстоит решать задачи, связанные с анализом графиков различных функций.
На ОГЭ часто встречаются задания, где необходимо определить свойства графиков, построить график функции или наоборот, по графику функции найти ее уравнение. Для успешного выполнения таких заданий необходимо хорошо знать свойства и особенности различных функций.
Один из ключевых типов функций, с которыми школьники сталкиваются на ОГЭ - это линейные функции. Они задаются уравнением y = kx + b, где k и b - это константы. Школьникам нужно уметь строить графики линейных функций и определять их уравнения по графику.
Другой тип функций, который встречается на ОГЭ - это параболы. Парабола задается уравнением y = ax^2 + bx + c. Школьники должны уметь строить графики парабол и определять их параметры по графику.
Еще одним важным типом функций являются прямоугольные гиперболы. Школьники должны уметь строить графики прямоугольных гипербол и определять их параметры.
Важно отметить, что умение анализировать графики функций и решать задачи, связанные с функциями, является важной компетенцией, необходимой для успешного прохождения ОГЭ по математике. Поэтому школьники должны тщательно изучать эту тему и отрабатывать различные типы заданий.
| Тип функции | Уравнение | Свойства графика |
|---|---|---|
| Линейная функция | y = kx + b | Прямая линия |
| Парабола | y = ax^2 + bx + c | Симметричная относительно оси y |
| Прямоугольная гипербола | y = a/x | Две асимптоты, симметрична относительно центра координат |
Понятие функции

Для того чтобы определить функцию, необходимо указать ее имя и правило определения. Обычно функции обозначаются буквами, например, f(x), g(x) и т.д. Здесь "x" - это переменная, которая принимает значения из области определения функции.
График функции - это геометрическое представление функции на плоскости. Обычно график функции представляет собой множество точек, координаты которых определяются значениями переменных из области определения и области значений функции. График функции может быть представлен в виде линии, кривой или дискретного набора точек.
На ОГЭ по прямой графики функций представлены на координатной плоскости. Ось абсцисс (x) представляет собой горизонтальную ось, а ось ординат (y) - вертикальную ось. Каждая точка на графике функции имеет свои координаты (x, y), где "x" - это значение переменной, а "y" - значение функции при этом значении переменной.
| Функция | График |
|---|---|
| f(x) = x |  |
| f(x) = x + 2 |  |
| f(x) = x^2 |  |
Как показано в приведенной таблице, каждая функция имеет свой график, который отображает зависимость между значениями переменной и значениями функции. Анализ графиков функций помогает понять и изучить их свойства, такие как возрастание, убывание, наличие экстремумов и т.д.
Как строить график функции
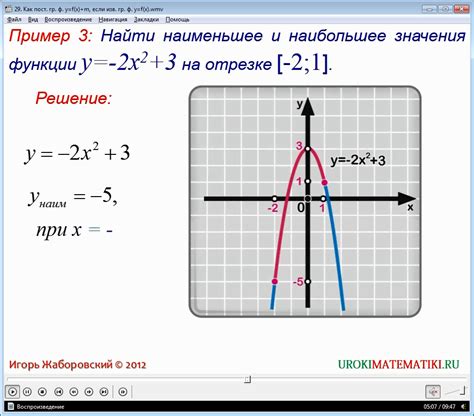
Шаг 1: Определение области определения функции. Область определения - это множество значений, для которых функция определена. На основе этого определяется интервал значений аргумента, на котором будет построен график.
Шаг 2: Выбор точек для построения графика. Обычно выбираются несколько значений аргумента, чтобы получить представление о поведении функции.
Шаг 3: Вычисление значений функции для выбранных точек. Подставляя значения аргумента в функцию, можно получить соответствующие значения функции, которые затем откладываются на графике.
Шаг 4: Построение графика на координатной плоскости. С помощью полученных значений функции откладываются точки на координатной плоскости и их соединяют линией. Это позволяет визуализировать форму графика и понять его основные свойства.
Шаг 5: Анализ графика. Исследуя график, можно получить информацию о поведении функции на выбранном интервале, такую как возрастание или убывание, экстремумы, периодичность и другие свойства.
Распределение функций на плоскости
Функции могут быть представлены различными математическими формулами. Некоторые функции могут быть заданы линейным уравнением, например y = kx + b, где k и b - это коэффициенты. Такие функции называются линейными, и их графики представляют собой прямую на плоскости.
Другие функции могут иметь более сложные формулы, например, степенные функции, экспоненциальные функции, тригонометрические функции и т.д. Графики таких функций могут иметь различные формы и располагаться на плоскости в разных областях.
При решении задач на ОГЭ по прямой, важно уметь строить графики функций в осях координат и анализировать их свойства. Например, для линейных функций, необходимо уметь определять наклон прямой, ее направление и точку пересечения с осями координат. Для других функций также требуется умение анализировать особенности их графиков и использовать их в решении задач.
Таким образом, функции и графики на плоскости тесно связаны между собой. Умение строить и анализировать графики функций поможет в решении задач на ОГЭ по прямой и в более сложных математических задачах. Поэтому важно не только понимать математические связи между функциями и графиками, но и научиться применять эти знания на практике.