Фигуры - это объекты, которые окружают нашу жизнь, пронизывают пространство и являются неотъемлемой частью нашего восприятия мира. Без них, наше представление о формах и структурах было бы неполным и ограниченным. Но даже в самом многообразном мире геометрических фигур существуют некоторые, которые выделяются и не подчиняются общим законам.
Когда мы говорим об "лишней" фигуре, мы подразумеваем, что она выделяется среди своих "собратьев", не вписывается в общую картину и не находит свое место в ее гармонии. Часто такие фигуры оказываются странными, неестественными или просто непонятными для нашего восприятия, вызывая чувство недовольства или недоумения.
Но откуда берется такое многообразие "лишних" фигур? Каждая из них - результат экспериментов человеческого воображения и творческого процесса. Иногда они могут быть ошибкой или простым перебором, а иногда - смелым выходом за рамки ожидаемого и стандартизации. Важно помнить, что те самые "лишние" фигуры могут стать источником вдохновения, новой точки зрения и исходной точки для развития новых идей в разных областях человеческой деятельности.
Эстетика формы

Каждая фигура представляет собой уникальную комбинацию линий, углов, изгибов и поверхностей. И хотя каждая фигура может быть красивой и впечатляющей по-своему, ее красота исходит из ее формы.
Форма является одной из самых важных составляющих эстетики фигуры. У нее может быть симметричная или асимметричная форма, простая или сложная. Форма может быть гладкой и изящной, или же иметь острые углы и резкие переходы. Но независимо от своего внешнего вида, каждая фигура обладает своими уникальными привлекательными чертами.
Форма фигуры может вызывать определенные чувства и эмоции у зрителя. Например, круглая форма может создавать ощущение гармонии и спокойствия, в то время как острые углы и геометрические линии могут вызывать ощущение силы и энергии.
Более того, форма фигуры может быть использована для передачи определенных идей и концепций. Например, фигура, состоящая из прямых, четких линий, может символизировать строгость и порядок, в то время как фигура, имеющая плавные и изогнутые линии, может передавать идею грации и элегантности.
В конечном счете, каждая фигура является уникальной и необычайно прекрасной в своей форме. От простейшего треугольника до сложнейшего полигона, каждая фигура имеет свое особое место в эстетике искусства. Именно поэтому каждую фигуру можно назвать лишней – потому что все они, простые и сложные, вносят свой вклад в общий хореографический ансамбль этого мира.
Все фигуры имеют свою уникальность
Каждая фигура в геометрии имеет свои особенности и характеристики, которые делают ее уникальной. Независимо от размера, формы или положения, каждая фигура может быть описана и классифицирована по определенным признакам.
- Круг - единственная фигура, у которой все точки находятся на одинаковом расстоянии от центра. Он не имеет углов и сторон, что делает его особенным среди других фигур.
- Квадрат - фигура с четырьмя равными сторонами и четырьмя прямыми углами. Именно благодаря своим четким границам и прямым углам, квадрат используется во множестве приложений, включая архитектуру и дизайн.
- Треугольник - фигура с тремя сторонами и тремя углами. Зависимо от длин сторон и величины углов, треугольники могут быть равносторонними, равнобедренными или разносторонними, что делает их разнообразными и интересными.
- Прямоугольник - фигура с четырьмя прямыми углами и противоположными сторонами, которые равны по длине. Прямоугольники широко используются в разных сферах, начиная от строительства и заканчивая играми и графикой.
- Параллелограмм - фигура с двумя параллельными сторонами и двумя углами. Он обладает уникальной особенностью – противоположные стороны параллелограмма равны между собой и параллельны.
Таким образом, каждая фигура в геометрии обладает своей уникальностью и применяется в различных сферах нашей жизни. Изучение и понимание характеристик каждой фигуры помогает нам лучше понять мир вокруг нас и использовать его в наших интересах.
Как формы влияют на восприятие

Каждая форма передает определенное сообщение и вызывает определенные эмоции у пользователей. Например, прямоугольные формы могут выглядеть стабильно и надежно, а круглые формы – мягко и гармонично.
Формы также могут изменяться в зависимости от контекста использования. Например, веб-сайты, связанные с технологиями, часто используют угловые и симметричные формы, чтобы подчеркнуть строгость и точность технологических процессов. В то же время, веб-сайты, связанные с природой или искусством, часто используют органические, изящные и несимметричные формы для передачи эмоциональной и творческой атмосферы.
О выборе формы следует думать, исходя из целей проекта и целевой аудитории. Адаптивный и дружелюбный дизайн, созданный с учетом этих факторов, поможет привлечь и удержать внимание пользователей, а также создать положительные эмоции и ассоциации.
Математическая точка зрения

Например, треугольник является одной из простейших и наиболее изученных фигур. Он имеет три стороны и три угла. Треугольники могут быть равносторонними, равнобедренными или разносторонними. Каждый из этих типов треугольников обладает своими особенностями и свойствами.
Круг, с другой стороны, является фигурой без сторон и углов. Он обладает радиусом, диаметром и центром. Круг также имеет свои специальные свойства, например, формула для вычисления его площади или длины окружности.
Следовательно, каждая фигура имеет свое место и значение в математике. Нельзя сказать, что одна из них лишняя, так как каждая из фигур имеет свою уникальную геометрическую структуру и свойство, которые позволяют нам изучать и понимать мир вокруг нас.
Геометрическое равенство всех фигур
Геометрические фигуры могут быть различными: треугольниками, квадратами, прямоугольниками, окружностями и так далее. Несмотря на их разнообразие, каждая из них может быть расценена как лишняя.
Например, возьмем треугольник. Представим себя в геометрической области, где все треугольники равны между собой. В таком случае, нам не важно, какой именно треугольник мы рассматриваем, все они будут геометрически равны. И это относится ко всем фигурам – они равнозначны друг другу в геометрическом смысле.
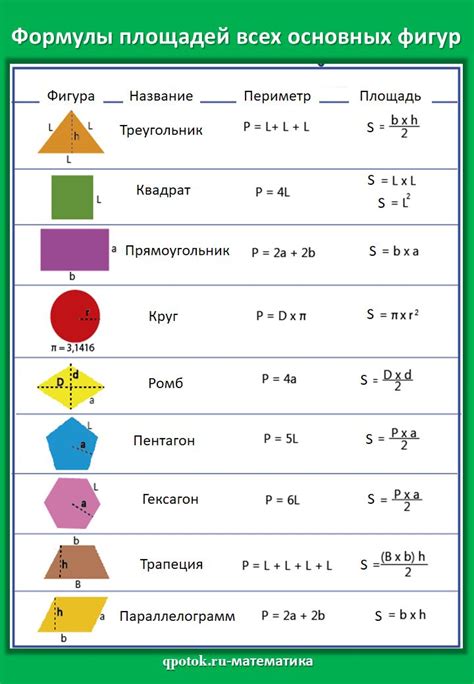
Чтобы проиллюстрировать это, рассмотрим таблицу, в которой перечислены различные геометрические фигуры и их параметры:
| Фигура | Параметры |
|---|---|
| Треугольник | Три стороны, три угла |
| Квадрат | Четыре стороны, четыре угла |
| Прямоугольник | Два параллельных противоположных стороны, четыре угла |
| Окружность | Радиус, диаметр, центр |
| И еще множество других фигур | ... |
Как видно из приведенной таблицы, у каждой фигуры есть свои особенности и параметры. Но несмотря на это, все они имеют общую основу геометрического равенства.
Таким образом, каждую фигуру можно назвать лишней, потому что в геометрии все фигуры могут быть сведены к общей основе и рассмотрены как эквивалентные друг другу.