Карл Фридрих Гаусс - одна из самых знаменитых фигур в мире математики. Его гениальность и вклад в различные области математики сделали его одним из наиболее влиятельных ученых всех времен. Как родившийся в Германии математик и физик, Гаусс был известен своими открытиями в таких областях, как арифметика, анализ, геометрия, теория чисел и многих других.
Карл Фридрих Гаусс родился 30 апреля 1777 года в крошечном городе Брауншвейг в Германии. Уже с раннего возраста Гаусс демонстрировал незаурядные способности в математике, и его таланты были замечены его учителем в местной школе. Его математический гений не прошел незамеченным, и в 1795 году он поступил в Готтингенский университет, где его способности были признаны и оценены.
Наиболее известными работами Гаусса стали его работы в области арифметики. Он совершил ряд важных открытий, включая закон Гаусса для электричества, целочисленную аппроксимацию и метод наименьших квадратов. Он также разработал гипотезу о распределении простых чисел, которая стала известна как гипотеза Гаусса.
Карл Фридрих Гаусс - гений математики и его вклад в науку

Карл Фридрих Гаусс, также известный под именем Иоганн Карл Фридрих Гаусс, был немецким математиком, физиком, астрономом и статистиком. Он считается одним из наиболее влиятельных математиков в истории и сделал значительный вклад в такие области, как алгебра, теория чисел, геодезия, астрономия и физика.
Родился в Брауншвейге, Германия, 30 апреля 1777 года, Гаусс проявил удивительный математический талант с ранних лет. Его способности были замечены учителем в местной школе, который в свою очередь добился для него стипендии и поступления в Духовную школу Карла Готфрида Зейдла, где Гаусс был открыт для широкого спектра математических и научных идей.
Один из самых известных вкладов Гаусса в науку - его работы в области алгебры и теории чисел. Он разработал многочисленные теоремы и методы, которые привнесли значительный прогресс в этих областях математики. Например, он впервые доказал фундаментальную теорему алгебры, которая утверждает, что всякое ненулевое алгебраическое уравнение имеет хотя бы один комплексный корень.
В дополнение к своей работе в алгебре и теории чисел, Гаусс также внес важные вклады в физику и астрономию. Он разработал теорию движения небесных тел, которая стала основой для современной астрономии. Он также изучал магнетизм и электричество и сделал значительные открытия в этой области.
Гаусс был удостоен множества наград за свою работу, включая королевский орден Пруссии и почетное членство в Королевском обществе Лондона. Его работы до сих пор остаются важными и влиятельными в мире математики и науки в целом.
| Дата рождения | 30 апреля 1777 года |
|---|---|
| Место рождения | Брауншвейг, Германия |
| Сферы деятельности | Математика, физика, астрономия, статистика |
| Известные достижения | Разработка фундаментальной теоремы алгебры, разработка теории движения небесных тел |
Ранние годы и образование Гаусса, его ранние достижения

Карл Фридрих Гаусс родился 30 апреля 1777 года в Брюнсвике, Германии. Уже в раннем детстве, он показался необычные математические способности. В 1788 году, в возрасте 11 лет, Гаусс учитель заметил его математический талант и посоветовал его родителям отправить его в школу, где он мог бы развить свои способности.
В 1792 году, в возрасте 15 лет, Гаусс поступил в Гимназию Каролины в Брюнсвике. Здесь он стал пристально интересоваться математикой и заметно превосходил своих одноклассников в этой области. Гаусс самостоятельно изучал математические работы и решал сложные задачи.
Одним из ранних достижений Гаусса было открытие метода нахождения сумм арифметических прогрессий в 1796 году, когда ему было всего 19 лет. Этот метод был значительным прорывом в математике и привел к признанию Гаусса как одного из величайших математиков своего времени.
Также Гаусс занимался изучением теории чисел и доказал несколько важных теорем в этой области. В 1801 году, в возрасте 24 лет, Гаусс опубликовал свою работу "Дискуссии" (Disquisitiones Arithmeticae), в которой он систематизировал результаты своих исследований и сформулировал теоремы, которые стали основой для дальнейшего развития теории чисел.
Ранние достижения Карла Фридриха Гаусса привлекли внимание ученых и математиков со всего мира, и он был назначен профессором математики в Геттингенском университете в 1807 году. Там он продолжил свои исследования и сделал еще более значимые открытия, которые заслуживают особого внимания и признания.
Открытие Гауссом законов закрепления заряда и составление нормального распределения
Карл Фридрих Гаусс был выдающимся немецким математиком, который внес значительный вклад в различные области науки. Одним из его важных открытий были законы закрепления заряда, которые описывают взаимосвязь между электрическими зарядами в системе.
Согласно законам закрепления заряда, электрический заряд на поверхности закрытой системы распределяется равномерно. Это означает, что сумма всех зарядов на поверхности системы равна нулю. Этот результат был важным открытием в области электростатики и помог Гауссу развить концепцию электрических полей и потенциалов.
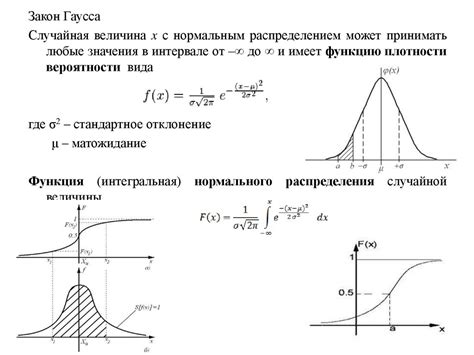
Кроме того, Гаусс занимался разработкой нормального распределения, который также известен как "закон Гаусса". Он создал математическую модель, описывающую распределение данных в небольшой выборке вокруг среднего значения. Нормальное распределение встречается в различных сферах, таких как статистика, физика, экономика и другие, и широко используется для анализа данных и прогнозирования.
Открытия Гаусса в области законов закрепления заряда и нормального распределения имели глубокое влияние на развитие науки и применяются во множестве областей исследования и практического применения.
Вклад Гаусса в астрономию и квадратичную форму, его работы над функциями и эллиптическими интегралами

Карл Фридрих Гаусс, выдающийся немецкий математик, внес значительный вклад в различные области науки, включая астрономию и квадратичную форму. Его работы в этих областях оказали огромное влияние на развитие математики и физики.
В астрономии Гаусс совершил многочисленные открытия и предложил новые методы расчета для определения орбит планет и астероидов. Он разработал методы для определения и анализа орбит и траекторий движения небесных тел, включая метод минимальных квадратов. Его работы позволили точно предсказывать движение планет и астероидов в Солнечной системе и дали толчок к развитию астрономии как науки.
Однако, одной из самых важных тем, к которым Гаусс внес вклад, была квадратичная форма. Он разработал методы решения квадратичных уравнений и впервые опубликовал свои результаты в 1799 году, в своей диссертации «Дискуссии кругами на проблему с разрешимостью в уравнениях». Его работы по квадратичной форме имели революционное значение и положили основы для его дальнейшей работы и значительных открытий в области математики и физики.
Гаусс также работал над функциями и эллиптическими интегралами. В его работе «Функции Эллиптические» Гаусс предложил новые методы для решения сложных интегральных уравнений, связанных с эллиптическими функциями. Его работы в этой области считаются известными и влиятельными в истории математики. Гаусс внес значительный вклад в развитие эллиптических функций и их применение в различных областях науки и техники.
Итак, вклад Карла Фридриха Гаусса в астрономию и квадратичную форму, его работы над функциями и эллиптическими интегралами оказали огромное влияние на математику и физику. Его открытия и результаты работы стали фундаментом для дальнейших исследований и развития науки в этих областях.
Гаусс и его вклад в теорию чисел, работа над простыми и составными числами

Карл Фридрих Гаусс, один из самых выдающихся математиков всех времен, внес огромный вклад в развитие теории чисел. Он разработал многочисленные теоремы, которые стали основой для дальнейших исследований и применений в этой области.
Одной из главных работ Гаусса в теории чисел была его теорема о целых числах. Согласно этой теореме, каждое целое число может быть разложено на простые множители с единственностью. Это дало возможность более эффективно работать с числами и доказывать различные теоретические утверждения.
Гаусс также работал над исследованием простых и составных чисел. Он разработал множество алгоритмов и методов для нахождения простых чисел, а также для определения, является ли число составным. Эти методы были использованы им самим и стали основой для дальнейших исследований математиков в этой области.
Он доказал закон закономерностей распределения простых чисел, который впоследствии стал одной из важных теорем в теории чисел. Гаусс также провел исследования над суммой простых чисел, которые положили основу для работы других математиков в этом направлении.
Вклад Гаусса в теорию чисел был огромен и его работы оказали огромное влияние на дальнейшее развитие этой области. Его идеи и методы стали фундаментом для многих теоретических и практических приложений в математике и криптографии.
Гаусс и его влияние на развитие физики и статистики, создание метода наименьших квадратов

Карл Фридрих Гаусс был не только выдающимся математиком, но и оказал значительное влияние на развитие физики и статистики. Его работы имели широкое применение и до сих пор используются в научных и инженерных исследованиях.
Одним из наиболее важных достижений Гаусса было создание метода наименьших квадратов. Этот метод является неотъемлемой частью статистики и позволяет сократить ошибку при аппроксимации данных. Суть метода заключается в минимизации суммы квадратов отклонений между наблюдаемыми значениями и значениями, предсказанными линейной моделью. Это позволяет получить наилучшую приближенную прямую или кривую, проходящую через точки на графике.
Метод наименьших квадратов применяется в различных областях, включая физику, экономику, биологию и другие науки. Он позволяет анализировать и интерпретировать экспериментальные данные, устанавливать закономерности и взаимосвязи в исследуемых явлениях.
В физике метод наименьших квадратов используется, например, для подбора параметров в математических моделях, описывающих физические процессы. Он позволяет установить взаимосвязь между измеряемыми величинами и построить эмпирическое представление о физическом явлении.
Таким образом, благодаря своему вкладу в развитие метода наименьших квадратов, Гаусс позволил облегчить и усовершенствовать анализ данных в научных исследованиях, а также внести значительный вклад в развитие физики и статистики в целом.
Завершение научной карьеры Карла Фридриха Гаусса и его научное наследие

После долгих лет плодотворной научной работы, Карл Фридрих Гаусс решил постепенно сократить свою активность и завершить научную карьеру. Он стал выделять больше времени на образовательные и социальные проекты, а также на изучение философии и истории. В своих последних годах он также заинтересовался астрономией и занимался изучением движения планет и составлением астрономических таблиц.
Научное наследие Карла Фридриха Гаусса огромно. Он сделал важные открытия в различных областях математики, физики и астрономии. В частности, его работы в области теории чисел, теории вероятности и астрономии стали фундаментом для дальнейших разработок и нашли широкое применение. Его наиболее известной работой является "Дискретная лемма Гаусса", которая стала одним из важнейших результатов в теории чисел.
Гаусс также внес значительный вклад в области электромагнетизма и геодезии. Он разработал теорию электромагнитного поля, которая стала основой для будущих исследований в этой области. В области геодезии он разработал новые методы и инструменты для измерения земной поверхности, включая известную "арифметическую геодезическую среднюю". Сегодня эти разработки продолжают использоваться в современной науке и инженерии.
Карл Фридрих Гаусс оставил огромное научное наследие, которое до сих пор является объектом исследования и восхищения для ученых со всего мира. Его вклад в математику и естественные науки будет оцениваться еще многие годы, и его имя будет навсегда связано с триумфами разума и научного прогресса.