Теорема Пифагора – одно из основных математических утверждений, которое позволяет находить длину третьего катета треугольника, если известны длины двух других катетов.
Согласно этой теореме, квадрат длины гипотенузы (самого длинного из трех сторон треугольника) равен сумме квадратов длин катетов (двух меньших сторон).
Формула Пифагора выглядит следующим образом: c² = a² + b², где "c" - длина гипотенузы, "a" и "b" - длины катетов.
Из этой формулы можно вывести два вида задач: нахождение длины гипотенузы по известным длинам катетов и нахождение длины одного из катетов, если известны длины другого катета и гипотенузы.
Решение задач с катетами треугольника по формуле Пифагора может быть полезным при работе с различными фигурами, а также в повседневной жизни. Зная эту формулу, можно легко и быстро находить длину сторон треугольников и решать соответствующие задачи.
Нахождение длины катета треугольника
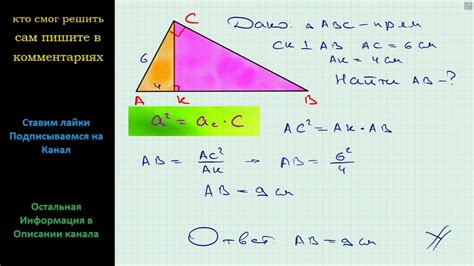
Для нахождения длины катета треугольника можно использовать формулу Пифагора. Формула Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Используя эту формулу, мы можем найти длину одного из катетов треугольника, если известны длины гипотенузы и другого катета.
Для нахождения длины катета, сначала возводим длину гипотенузы в квадрат, а затем вычитаем из этого значения квадрат длины известного катета. Результатом будет квадрат длины неизвестного катета. Чтобы найти длину катета, нужно извлечь квадратный корень данного значения.
Или можно использовать формулу: катет = √(гипотенуза^2 - катет^2), где катет - длина неизвестного катета, гипотенуза - длина гипотенузы, катет - длина известного катета.
Таким образом, зная длину гипотенузы и одного из катетов треугольника, мы можем легко найти длину другого катета, используя формулу Пифагора.
Метод Пифагора для нахождения катета

Для нахождения катета по методу Пифагора нужно знать длины гипотенузы и другого катета. Формула выглядит следующим образом:
Катет = квадратный корень(гипотенуза2 - катет2)
Для примера, пусть у нас есть прямоугольный треугольник, в котором длина гипотенузы равна 5 и длина одного из катетов равна 3. Применяя метод Пифагора, мы можем найти длину второго катета:
Катет = квадратный корень(52 - 32)
Катет = квадратный корень(25 - 9)
Катет = квадратный корень(16)
Катет = 4
Таким образом, второй катет имеет длину 4.
Метод Пифагора является важным инструментом для решения задач, связанных с прямоугольными треугольниками. Этот метод позволяет находить недостающие стороны треугольника и применяется в различных областях, включая геометрию, физику и инженерию.
Использование теоремы Пифагора для решения задач
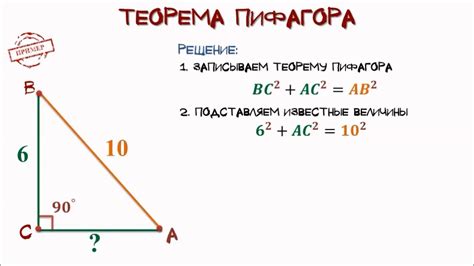
Формула Пифагора устанавливает связь между длинами катетов a и b и гипотенузой c:
c2 = a2 + b2
Эта формула обеспечивает нам возможность решать задачи, связанные с нахождением длины одного из катетов или гипотенузы прямоугольного треугольника, если известны значения двух других сторон.
Чтобы использовать формулу Пифагора для решения задач, сначала нужно определить, что является гипотенузой, а что – катетами. Гипотенуза – это самая длинная сторона треугольника, и она всегда располагается напротив прямого угла. Катеты – это две другие стороны треугольника.
Для решения задач с теоремой Пифагора, сначала нужно представить условие задачи в виде уравнения с использованием формулы Пифагора. Затем, зная два значения (катеты или гипотенузу), можно выразить третье значение с помощью алгебраических операций. Зная значения двух сторон, мы можем подставить их в формулу Пифагора и решить получившееся уравнение для нахождения третьей стороны.
Таким образом, использование теоремы Пифагора позволяет эффективно решать задачи, связанные с нахождением и взаимосвязью длин катетов и гипотенузы прямоугольных треугольников.
Примеры задач, в которых используется формула Пифагора

Рассмотрим несколько примеров задач, в которых используется формула Пифагора:
| Пример | Задача | Решение |
|---|---|---|
| Пример 1 | В прямоугольном треугольнике один из катетов равен 3, а гипотенуза равна 5. Найдите второй катет. | По формуле Пифагора: a^2 + b^2 = c^2. Подставляем известные значения: 3^2 + b^2 = 5^2. Решаем уравнение: 9 + b^2 = 25. Вычитаем 9: b^2 = 16. Извлекаем корень: b = 4. |
| Пример 2 | В треугольнике один из катетов равен 7, а гипотенуза равна 25. Найдите второй катет. | По формуле Пифагора: a^2 + b^2 = c^2. Подставляем известные значения: 7^2 + b^2 = 25^2. Решаем уравнение: 49 + b^2 = 625. Вычитаем 49: b^2 = 576. Извлекаем корень: b = 24. |
| Пример 3 | В треугольнике один из катетов равен 12, а второй катет равен 16. Найдите длину гипотенузы. | По формуле Пифагора: a^2 + b^2 = c^2. Подставляем известные значения: 12^2 + 16^2 = c^2. Вычисляем: 144 + 256 = c^2. Складываем: 400 = c^2. Извлекаем корень: c = 20. |
Это лишь несколько примеров задач, в которых применяется формула Пифагора. Используя эту формулу, можно решать множество различных задач, связанных с прямоугольными треугольниками.
Нахождение гипотенузы треугольника
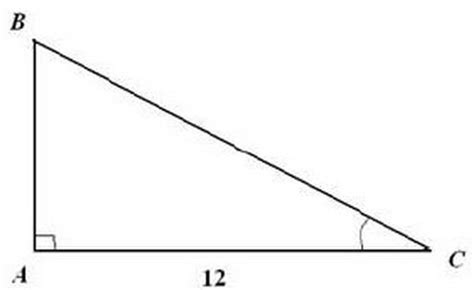
Теорема Пифагора: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, если длины катетов a и b известны, то длина гипотенузы c может быть найдена с помощью формулы:
c = √(a² + b²)
Пример: Для треугольника с катетами a = 3 и b = 4, можно найти гипотенузу c следующим образом:
c = √(3² + 4²) = √(9 + 16) = √25 = 5
Таким образом, длина гипотенузы треугольника равна 5.
Нахождение гипотенузы треугольника по формуле Пифагора очень полезно при решении задач, связанных с прямоугольными треугольниками. Используя эту формулу, можно легко вычислить длины сторон и решить различные задачи.
Простые шаги для нахождения гипотенузы

Нахождение длины гипотенузы треугольника может быть легкой задачей, если вы знаете длины обоих катетов. Для этого можно воспользоваться формулой Пифагора.
Шаги для нахождения гипотенузы:
- Запишите известные значения. Обозначьте длины катетов, которые вам уже известны. Назовите их a и b.
- Используйте формулу Пифагора. Согласно этой формуле, квадрат длины гипотенузы (c) равен сумме квадратов длин катетов (a2 + b2). Таким образом, формула будет выглядеть так: c2 = a2 + b2.
- Вычислите значение гипотенузы. Для этого возведите каждое известное значение в квадрат и сложите их. Затем извлеките квадратный корень из суммы, чтобы получить длину гипотенузы.
Теперь у вас есть простые шаги для нахождения длины гипотенузы треугольника по формуле Пифагора. Зная значения катетов, вы сможете легко вычислить длину гипотенузы и использовать эту информацию при решении различных задач.
Приложение формулы Пифагора для решения задач
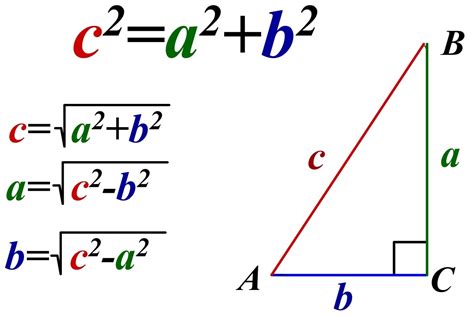
Применение формулы Пифагора особенно полезно при решении задач о прямоугольных треугольниках. Если известны длины двух катетов, то для нахождения гипотенузы в формулу подставляются значения длин катетов и производят вычисления.
Также формула Пифагора может быть использована для определения длины катета, если известны длины гипотенузы и другого катета. Для этого в формулу подставляются значения длины гипотенузы и одного из катетов, и завершают вычисления.
Знание и применение формулы Пифагора позволяет решать множество задач, связанных с треугольниками, простым и эффективным способом. Она является одним из основных инструментов геометрии и находит применение в различных областях науки и техники.
Расчет гипотенузы в практических примерах
Например, представим себе ситуацию, когда нам необходимо определить длину провода, который нужно закупить для обвязки деревьев вдоль участка. Пусть мы знаем длину одного катета, равную 5 метров, и второго катета, равную 12 метров. Используя формулу Пифагора, мы можем легко найти длину гипотенузы: сумма квадратов катетов равна квадрату гипотенузы. Итак, 5² + 12² = гипотенуза². Решив данное уравнение, получаем, что гипотенуза равна √(5² + 12²) = √(25 + 144) = √169 = 13 метров.
Рассмотрим еще один пример. Допустим, нам необходимо определить длину наклонной опоры для трубопровода, который будет проложен между двумя точками на различных уровнях земли. Представим, что первая точка находится на высоте 15 метров, а вторая точка находится на высоте 9 метров. Используя формулу Пифагора, найдем длину наклонной опоры. Сумма квадратов катетов равна квадрату гипотенузы: 15² + 9² = гипотенуза². Решив данное уравнение, получаем, что гипотенуза равна √(15² + 9²) = √(225 + 81) = √306 = 17.5 метров.
Таким образом, формула Пифагора является мощным инструментом для решения практических задач, связанных с нахождением гипотенузы треугольника. Она позволяет легко и быстро вычислять неизвестные величины на основании известных данных о катетах. Это может быть полезно в различных сферах деятельности, начиная от строительства и геодезии, и заканчивая использованием в повседневной жизни.
Практическое использование формулы Пифагора

Применение формулы Пифагора особенно полезно для решения задач, связанных с построением и измерением различных объектов. Например, можно использовать эту формулу для определения длины троса, необходимого для подвешивания объекта, зная расстояние между точками крепления и высоту подвеса.
Также формула Пифагора широко применяется в строительстве и архитектуре. Ее можно использовать для определения длины перегородок или кабельных линий, а также для расчета габаритов и плоскостей в различных конструкциях. Формула Пифагора позволяет точно определить размеры и углы при изготовлении и монтаже разнообразных объектов.
Кроме того, формула Пифагора часто применяется в тригонометрии. С ее помощью можно выразить тригонометрические функции через катеты и гипотенузу прямоугольного треугольника и наоборот.
Важно отметить, что формула Пифагора является основой для решения многих задач в различных областях науки и техники. Ее применение позволяет с легкостью находить значения неизвестных сторон треугольника и рассчитывать различные параметры объектов на основе известных данных.
| Известные значения сторон | Найденная сторона |
|---|---|
| Катет a = 3, катет b = 4 | Гипотенуза c = 5 |
| Гипотенуза c = 5, катет a = 3 | Катет b = 4 |
| Гипотенуза c = 5, катет b = 4 | Катет a = 3 |
Пример использования формулы Пифагора в архитектуре

Один из примеров использования формулы Пифагора в архитектуре – расчет размеров дверных проемов. Представьте, что вы архитектор и хотите спроектировать входную дверь для дома. Вам известны ширина и высота дверного проема, но вам нужно определить длину диагонали, чтобы правильно выбрать дверь.
Используя формулу Пифагора, вы можете найти длину диагонали следующим образом:
a2 + b2 = c2
Где: a и b – длины катетов (ширина и высота дверного проема), а c – длина диагонали.
Пример:
Измерим ширину дверного проема – 90 см, и высоту – 210 см. Теперь применим формулу Пифагора:
a2 + b2 = c2
902 + 2102 = c2
8100 + 44100 = c2
52200 = c2
c = √52200 ≈ 228,255
Таким образом, длина диагонали дверной проема составляет примерно 228,255 см. Эта информация позволит вам выбрать подходящую дверь, которая полностью закроет проем и создаст эстетически приятное впечатление.
Формула Пифагора – это незаменимый инструмент для архитекторов, помогающий расчитывать и пропорционально строить различные конструкции. Знание и применение этой формулы позволяет создавать гармоничные и функциональные архитектурные решения.