Параллелограмм – одна из самых интересных и сложных геометрических фигур, которая встречается в нашей повседневной жизни. В своей основе он объединяет два важных свойства: параллельность сторон и равенство противоположных углов.
Но что еще интересно о параллелограммах? Какие свойства скрываются внутри этих удивительных фигур? Одним из самых удивительных и невероятных свойств параллелограмма является его возможность превратиться в прямоугольник.
Может показаться странным, но каждый параллелограмм может стать прямоугольником, и это доказуемо. В данной статье мы рассмотрим доказательство этого факта и расскажем о связи между параллелограммами и прямоугольниками.
Определение и свойства параллелограмма
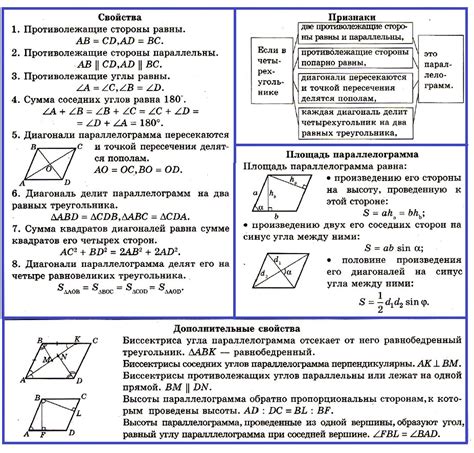
Свойства параллелограмма:
- Противоположные стороны параллелограмма равны по длине.
- Противоположные стороны параллелограмма параллельны.
- Сумма углов параллелограмма составляет 360 градусов.
- Диагонали параллелограмма делятся пополам и являются взаимно перпендикулярными.
Соотношения сторон и углов в параллелограмме

В параллелограмме существуют ряд характеристик, которые связывают его стороны и углы. Рассмотрим эти соотношения подробнее:
1. Противолежащие стороны параллелограмма равны между собой. Это значит, что AB = CD и BC = AD.
2. Противолежащие углы параллелограмма равны между собой. То есть ∠A = ∠C и ∠B = ∠D.
3. Сумма углов параллелограмма всегда равна 360 градусов. Таким образом, ∠A + ∠B + ∠C + ∠D = 360°.
4. Дополнительные углы параллелограмма также равны между собой. Это означает, что ∠A + ∠B = 180° и ∠C + ∠D = 180°.
| Storona AB | Storona BC | Storona CD | Storona AD |
| Angle ∠A | Angle ∠B | Angle ∠C | Angle ∠D |
Углы и диагонали параллелограмма
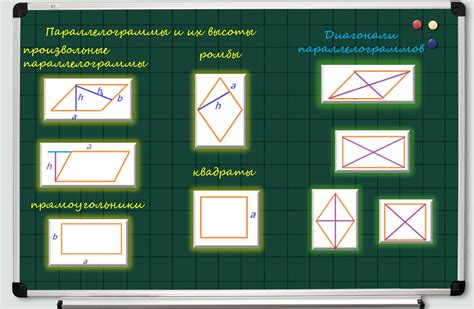
Углы:
1. Противоположные углы параллелограмма равны. Это значит, что угол A равен углу C, и угол B равен углу D.
2. Сумма углов параллелограмма равна 360 градусов. Следовательно, угол A + угол B + угол C + угол D = 360°.
Диагонали:
1. В параллелограмме существуют две диагонали - AC и BD.
2. Диагонали параллелограмма делятся пополам. Это значит, что длина отрезка AD равна длине отрезка BC и длина отрезка AB равна длине отрезка CD.
3. Диагонали параллелограмма делят его на два равных треугольника. Точка пересечения диагоналей делит каждый из треугольников на два равных подтреугольника.
| Свойство | Описание |
|---|---|
| Противоположные углы | Углы A и C равны, углы B и D равны |
| Сумма углов | Угол A + угол B + угол C + угол D = 360° |
| Диагонали | Диагонали AC и BD |
| Деление диагоналей | Отрезок AD = Отрезок BC, отрезок AB = Отрезок CD |
| Деление на треугольники | Диагонали делят параллелограмм на два равных треугольника |
Связь между углами и сторонами параллелограмма
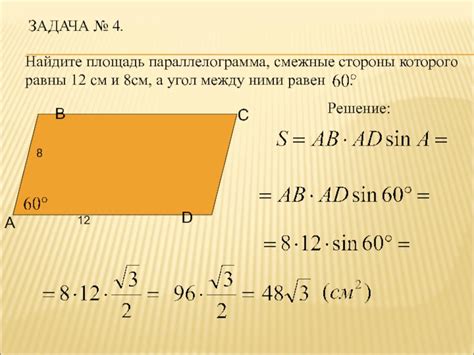
1. Противоположные стороны параллелограмма равны по длине. Это следует из определения параллелограмма, которое говорит о том, что противоположные стороны параллельны и равны между собой.
2. Противоположные углы параллелограмма равны. Если мы проведем диагональ в параллелограмме, то она разделит его на два равных треугольника. В этих треугольниках углы, лежащие при основаниях, будут равными, так как соответствующие стороны равны.
3. Сумма углов параллелограмма равна 360 градусам. Для доказательства этого факта можно воспользоваться свойством параллельных линий. Если мы проведем параллельные линии через противоположные углы параллелограмма, то получим две пары соответственных углов. Они будут равными, так как сами параллельные линии являются замечательным примером соответственных углов.
4. Диагонали параллелограмма делятся пополам и являются взаимно перпендикулярными. Если мы проведем диагонали в параллелограмме, то они пересекутся в точке, которая разделит каждую диагональ пополам. Также можно заметить, что диагонали пересекаются под прямым углом.
Изучая данные свойства параллелограмма, мы можем легко доказать, что каждый параллелограмм является прямоугольником. Комбинируя данные свойства, можно провести ряд доказательств, подтверждающих этот факт.
Периметр и площадь параллелограмма
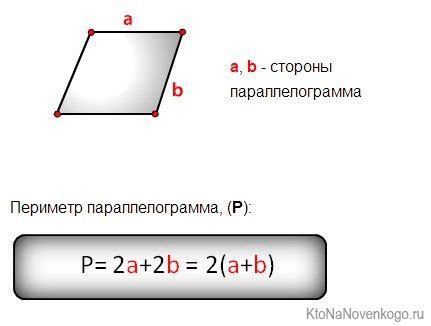
Периметр параллелограмма вычисляется по формуле:
Периметр = 2a + 2b, где a - длина основания, b - длина боковой стороны параллелограмма.
Площадь параллелограмма может быть найдена двумя способами:
- Первый способ: Площадь параллелограмма равна произведению длины основания на высоту, проведенную к этому основанию.
- Второй способ: Площадь параллелограмма равна произведению длины одной стороны на длину высоты, проведенной к этой стороне.
Оба способа дают одинаковый результат. Исходя из этих способов, формулы для вычисления площади параллелограмма могут быть записаны следующим образом:
Площадь = a * h = b * h, где a и b - длины сторон параллелограмма, h - высота, проведенная к основанию или боковой стороне параллелограмма.
Доказательство, что каждый параллелограмм - прямоугольник
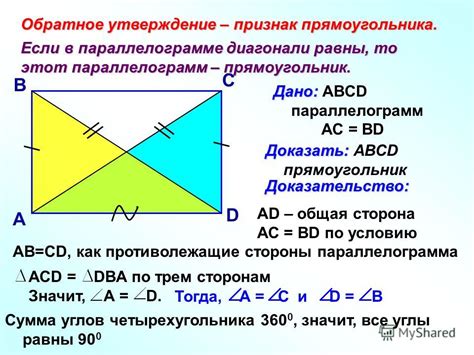
Доказательство этого факта можно провести, используя несколько геометрических свойств параллелограмма.
Во-первых, параллелограмм имеет две пары противоположных сторон, которые параллельны и равны по длине. Это означает, что углы между этими сторонами также равны. Помимо этого, параллелограмм также обладает свойством, что сумма углов при противоположных вершинах равна 180 градусов.
Однако, чтобы доказать, что каждый параллелограмм является прямоугольником, нам нужно проанализировать особый случай. Рассмотрим параллелограмм, у которого все углы прямые - прямоугольный параллелограмм.
Заметим, что в прямоугольном параллелограмме углы смежных сторон являются смежными углами. Также, поскольку углы смежных сторон равны 90 градусов, сумма углов при каждой вершине равна 360 градусов.
Теперь рассмотрим произвольный параллелограмм. Можно заметить, что любую сторону параллелограмма можно рассматривать как гипотенузу прямоугольного треугольника, образованного этой стороной и перпендикулярной к ней высотой.
Таким образом, каждый угол параллелограмма будет смежным к углу прямоугольного треугольника. Поскольку сумма углов при каждой вершине параллелограмма равна 360 градусов, и углы прямоугольного треугольника в сумме дают 90 градусов, то остальные два угла параллелограмма также должны быть прямыми.
Таким образом, мы доказали, что каждый параллелограмм является прямоугольником.
| Свойства параллелограмма | Свойства прямоугольника |
|---|---|
| Две пары противоположных сторон параллельны и равны | Две пары противоположных сторон параллельны и равны |
| Углы при противоположных вершинах равны | Углы при противоположных вершинах равны |
| Сумма углов при каждой вершине равна 360 градусов | Сумма углов при каждой вершине равна 360 градусов |
| Все углы равны 90 градусов |