Статистические таблицы являются важной частью анализа данных. Они предоставляют обобщенную информацию о различных переменных и распределениях в выборке. Одним из наиболее распространенных параметров, используемых для описания данных в статистике, является среднее значение или среднее арифметическое.
Среднее значение (или среднее арифметическое) - это мера центральной тенденции, которая показывает среднюю величину значений переменной. Для нахождения среднего значения статистической таблицы необходимо сложить все значения переменной и разделить их на общее количество значений. Это можно сделать вручную, используя калькулятор или же с помощью программного обеспечения для статистического анализа.
Однако, перед тем как находить среднее значение, необходимо уделить внимание предварительной обработке данных. Важно проверить наличие пропущенных значений и выбросов, а также провести необходимые преобразования, такие как удаление дубликатов или приведение данных к нужному формату. И только после этого можно приступить к нахождению среднего значения.
Среднее значение позволяет получить обобщенное представление о выборке и ее центральной тенденции. Однако следует помнить, что среднее значение чувствительно к выбросам и может искажать истинную картину данных. Поэтому важно проводить дополнительный анализ данных, такой как медиана или мода, для получения более полного и точного представления о распределении переменной в статистической таблице.
Определение понятия "среднее значение"

Среднее значение можно вычислить для различных типов данных, таких как числа, проценты, оценки, показатели и т.д. Оно широко используется в статистике, экономике, социологии, психологии и других областях, где требуется оценка среднего поведения или характеристики группы или выборки.
Среднее значение позволяет получить общую представление о данных и выявить их общую тенденцию или средний уровень. Оно может быть использовано для сравнения различных выборок или групп, а также для анализа изменений во времени или в разных условиях.
Известные методы вычисления среднего значения включают среднее арифметическое, среднее взвешенное, медиану и моду. Каждый из этих методов имеет свои преимущества и ограничения и может быть применим в различных ситуациях в зависимости от характеристик данных.
Однако следует помнить, что среднее значение может быть подвержено смещению, если выборка не представляет собой случайную или репрезентативную выборку из генеральной совокупности. Поэтому важно учитывать особенности данных и контекста, в котором они были собраны, при интерпретации среднего значения.
Способы нахождения среднего значения статистической таблицы
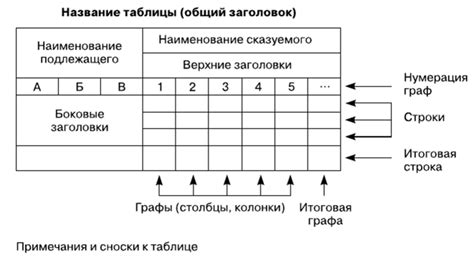
Среднее значение статистической таблицы представляет собой меру центральной тенденции, которая позволяет определить среднюю величину набора данных. Для нахождения среднего значения существуют различные методы, которые могут быть использованы в зависимости от характеристик статистической таблицы.
Один из самых простых способов нахождения среднего значения - это использование формулы для вычисления арифметического среднего. Для этого необходимо сложить все значения в статистической таблице и разделить полученную сумму на количество значений.
В некоторых случаях, когда значения в таблице содержат различные веса, может быть полезно использовать среднее взвешенное значение. Для его нахождения необходимо умножить каждое значение на соответствующий вес и найти сумму произведений. Затем полученную сумму необходимо разделить на сумму весов.
Если в статистической таблице присутствуют выбросы или значения сильно отклоняются от среднего, то для нахождения более устойчивого среднего значения можно использовать медиану. Медиана представляет собой значение, которое делит упорядоченный набор данных на две равные части. Медиану можно найти, упорядочив значения таблицы и выбрав значение посередине.
Для некоторых типов данных, таких как время или углы, используют среднее геометрическое или среднее гармоническое. Среднее геометрическое находится путем умножения всех значений и извлечения корня n-ой степени, где n - количество значений. Среднее гармоническое находится как обратное значение среднего арифметического от обратных значений.
В зависимости от конкретной задачи и характеристик данных, можно выбирать подходящий способ нахождения среднего значения статистической таблицы. В случае необходимости, можно также комбинировать различные методы для более точных результатов.
| Метод | Формула |
|---|---|
| Арифметическое среднее | (сумма значений) / (количество значений) |
| Взвешенное среднее | (сумма (значение * вес)) / (сумма весов) |
| Медиана | Выбирается значение посередине в упорядоченном наборе данных |
| Среднее геометрическое | Корень n-ой степени из произведения значений |
| Среднее гармоническое | Обратное значение среднего арифметического от обратных значений |
Математическое описание методов

Существует несколько методов для вычисления среднего значения статистической таблицы, каждый из которых имеет свои особенности и применяется в определенных ситуациях.
Один из наиболее распространенных методов - это вычисление среднего арифметического. Для этого необходимо умножить каждое значение из статистической таблицы на соответствующую ему частоту, затем сложить все произведения и разделить полученную сумму на сумму всех частот. Таким образом, можно получить среднее арифметическое значение.
Еще одним методом является вычисление среднего взвешенного значения. В этом случае, помимо значений и частот, учитывается еще и важность каждого значения. Вес каждого значения умножается на его частоту и затем складывается для всех значений. После этого полученная сумма делится на сумму всех весов и частот, что позволит получить среднее взвешенное значение.
Также существуют другие методы, такие как среднее геометрическое, среднее гармоническое и среднее квадратическое. Каждый из них находит применение в различных сферах, в зависимости от требуемого результата.
Важно помнить, что при вычислении среднего значения статистической таблицы необходимо учитывать все значения и соответствующие им частоты, чтобы результат был точным и репрезентативным.
Примеры применения:

Представим, что у нас есть статистическая таблица с данными о зарплатах работников в компании. В таблице указано количество работников в каждом возрастном диапазоне и их средняя зарплата. Нам необходимо найти среднюю зарплату по всей таблице.
1. Взвешенное среднее
Для этого нужно умножить каждое значение зарплаты на количество работников в этом возрастном диапазоне, затем сложить все полученные произведения и разделить на общее количество работников по всей таблице. Например, если у нас есть следующие данные:
| Возрастной диапазон | Количество работников | Средняя зарплата |
|---|---|---|
| 18-25 | 10 | 20000 |
| 26-35 | 20 | 25000 |
| 36-45 | 15 | 30000 |
Тогда расчет взвешенного среднего будет следующим:
(10 * 20000 + 20 * 25000 + 15 * 30000) / (10 + 20 + 15) = 25000
Таким образом, средняя зарплата по всей таблице составляет 25000.
2. Простое среднее
Если в таблице указано только количество работников в каждом возрастном диапазоне и средняя зарплата не представлена, можно найти простое среднее по формуле:
(Сумма всех зарплат) / (Количество работников)
Например, если у нас есть следующие данные:
| Возрастной диапазон | Количество работников |
|---|---|
| 18-25 | 10 |
| 26-35 | 20 |
| 36-45 | 15 |
А зарплаты равны: 20000, 25000, 30000. Тогда расчет простого среднего будет следующим:
(20000 + 25000 + 30000) / (10 + 20 + 15) = 25500
Таким образом, простое среднее значение зарплаты по всей таблице равно 25500.
Расчет среднего значения в статистической таблице
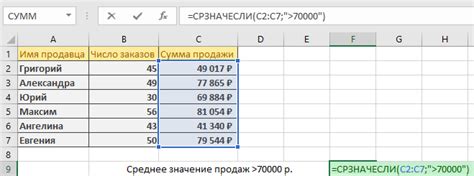
Среднее значение статистической таблицы позволяет получить общую характеристику данных и оценить их типичные значения. Для расчета среднего значения нужно умножить каждое значение в таблице на его частоту и полученные произведения сложить, а затем разделить сумму на общую частоту.
Для начала нужно определить столбец с данными и столбец с частотами в статистической таблице. Затем необходимо перейти к расчетам. Для этого нужно последовательно умножить каждое значение в столбце данных на соответствующую частоту и записать полученные произведения в отдельный столбец.
После этого нужно просуммировать значения в столбце произведений. Это даст общую сумму произведений. Наконец, общая сумма произведений делится на общую частоту, чтобы получить среднее значение статистической таблицы.
Применение метода расчета среднего значения в статистической таблице требует точных данных и внимательности при выполнении расчетов. Важно учесть, что результаты расчетов могут быть искажены в случае выбросов или несбалансированной выборки. Поэтому перед использованием метода рекомендуется провести анализ данных и проверить их корректность.
Важность нахождения среднего значения для анализа данных

Кроме того, среднее значение является важным при работе с большими объемами данных. Нахождение среднего значения позволяет суммировать информацию и представить ее в компактной форме. Это особенно полезно при анализе статистических таблиц или массивов числовых данных. Среднее значение предоставляет общую картину данных, и его изменение может указывать на наличие выбросов или неточностей.
Знание среднего значения также может быть полезно для принятия важных решений. Например, в бизнесе среднее значение может использоваться для определения рыночной стоимости товаров или услуг, установления цен, планирования бюджета и принятия других решений на основе анализа данных. Также среднее значение помогает сравнить фактические результаты с ожидаемыми, что позволяет оценить эффективность процессов и выявить потенциальные проблемы.
Все это подтверждает, что нахождение среднего значения имеет большую важность для анализа данных. Оно помогает представить информацию в удобной и понятной форме, выявить закономерности и тренды, сравнить различные группы или выборки данных, а также принять обоснованные решения на основе анализа данных.